堆&&堆排序&&优先级队列
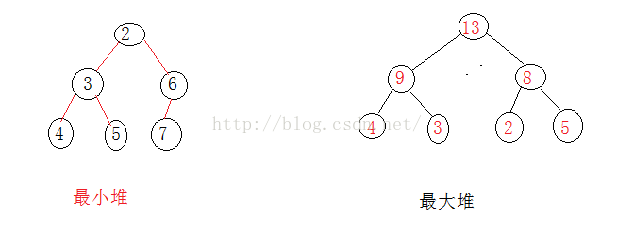
假设在一组数据集合中,每一个数据记录都有一个能标识自己的关键码。如果有一个关键码的集合,把这些关键码所表示的元素按照完全二叉树的顺序存储到一个一维数组中。如果所有父节点的关键码都小于或等于孩子的关键码,则称最小堆。如果父节点的关键码大于或等于孩子的关键码,则称最大堆。下面只介绍最小堆。
堆的性质:
1、可以通过一个简单的数组实现
2、支持最坏情况为O(logN)的insert和deleteMin
3、支持常量平均时间的insert操作以及常量平均最坏时间的findMin操作。
4、二叉堆是实现优先级队列的典型方法
堆所支持的基本操作:
template<typename T>
class BinaryHeap
{
typedef HeapNode<T> Node;
public:
BinaryHeap();
BinaryHeap(const vector<Node> &v);
void Insert(const Node& data);
void DeleteMin(Node& data = Node()); //删除最小元素,可以通过参数返回最小值
void MakeHeap(); //置空堆
bool IsEmpty()const; //判断堆是不是为空
const Node& findMin()const; //查找堆中的最小元素
protected:
void buildHeap(); //恢复堆的顺序
void percolate(int hole); //从hole开始下滑调整
protected:
vector<Node> _Heap; //存储的堆中元素的数组
int _Size; //标记堆中元素的个数
};
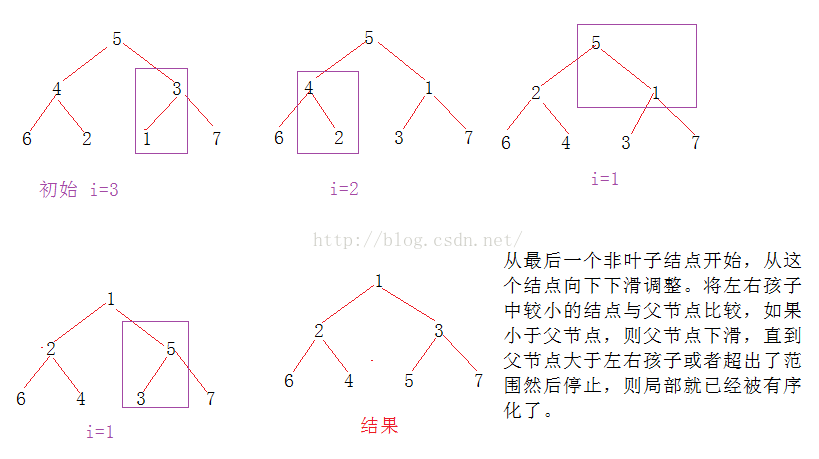
一、堆的建立
堆的建立有两种方式,一种是建立一个空堆,另一种是通过复制一个记录数组并对其加以调整形成一个堆。
BinaryHeap()
:_Heap(0)
, _Size(0)
{}
BinaryHeap(const vector<Node> &v)
:_Heap(v.size()+1) //为了便于计算,多开辟一个空间
, _Size(v.size())
{
for (int i = 1; i <=_Size; i++) //_Heap[0]不存放
{
_Heap[i] = v[i-1];
}
buildHeap();
}
在这里第一次为_Heap开辟v.size()+1个空间,将_Heap[0]浪费掉,从_Heap[1]开始存储,这样的化能够简化一下逻辑。不管是求父节点还是孩子节点亦或是求堆中第i个结点都能方便许多。
void buildHeap()是恢复堆中的顺序:
void buildHeap() //恢复堆的顺序
{
for (int i =_Size; i > 0; i--)
{
percolate(i);
}
}
void percolate(int hole)是从第hole个结点开始向下调整,使之在局部有序。
例:
void percolate(int hole) //从hole开始下滑调整
{
int child=0;
Node tmp = _Heap[hole];
for (;hole*2<=_Size;hole=child) //如果有左孩子则下滑调整
{
child = hole * 2;
if (child !=_Size&&_Heap[child]> _Heap[child + 1]) //找出左右孩子中值最小的
child++;
if (tmp < _Heap[child]) //如果tmp小于孩子的值,则调整结束
{
break;
}
else //如果tmp大于等于孩子的值,则继续调整
{
_Heap[hole] = _Heap[child];
}
}
_Heap[child] = tmp;
}
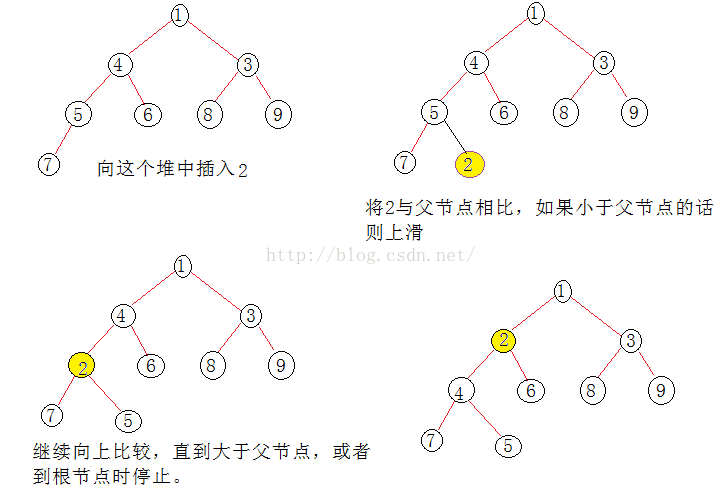
二、Insert操作
Insert所需要的是上滑调整,直接向_Heap中插入数据,然后通过上滑调整顺序。
例:
void Insert(const Node& data)
{
_Heap.push_back(data);
_Size++;
int i = _Size;
int parent= 0;
for (; i/2>0; i /= 2) //i这点的结点要有父亲节点
{
parent = i / 2; //父亲结点的位置
if (_Heap[parent] < data) //如果父亲结点比插入的值小,则有序
{
break;
}
else //如果父亲结点比插入值大
{
_Heap[i] = _Heap[parent];
}
}
_Heap[i] = data;
}
时间复杂度:O(lgN)
三、deleteMin操作
由于最小堆的性质,根节点总是最小值,所以将数组中最后一个结点的值放到根节点的位置,然后_Size自减,再从根节点开始进行一次下滑操作恢复堆的顺序。
void DeleteMin(Node& data=Node()) //删除最小元素,可以通过参数返回最小值
{
assert(_Size>0);
data = findMin();
_Heap[1] = _Heap[_Size--];
int i = 0;
percolate(1); //从根结点处开始下滑调整顺序
}
时间复杂度:O(lgN)
完整代码:
#pragma once
#include<cassert>
#include<vector>
template<typename T>
struct HeapNode
{
T _data;
size_t _key;
HeapNode()
{}
HeapNode(const T& data,size_t key)
:_data(data)
, _key(key)
{}
friend ostream& operator<<(ostream& os,const HeapNode<T>& heap)
{
os << heap._data;
return os;
}
friend bool operator>(const HeapNode<T>& h1,const HeapNode<T>& h2)
{
if (h1._key > h2._key)
return true;
else
return false;
}
friend bool operator<(const HeapNode<T>& h1, const HeapNode<T>& h2)
{
if (h1._key < h2._key)
return true;
else
return false;
}
};
template<typename T>
class BinaryHeap
{
typedef HeapNode<T> Node;
public:
BinaryHeap()
:_Heap(0)
, _Size(0)
{}
BinaryHeap(const vector<Node> &v)
:_Heap(v.size()+1) //为了便于计算,多开辟一个空间
, _Size(v.size())
{
for (int i = 1; i <=_Size; i++) //_Heap[0]不存放
{
_Heap[i] = v[i-1];
}
buildHeap();
}
void Insert(const Node& data)
{
_Heap.push_back(data);
_Size++;
int i = _Size;
int parent= 0;
for (; i/2>0; i /= 2) //i这点的结点要有父亲节点
{
parent = i / 2; //父亲结点的位置
if (_Heap[parent] < data) //如果父亲结点比插入的值小,则有序
{
break;
}
else //如果父亲结点比插入值大
{
_Heap[i] = _Heap[parent];
}
}
_Heap[i] = data;
}
void DeleteMin(Node& data=Node()) //删除最小元素,可以通过参数返回最小值
{
assert(_Size>0);
data = findMin();
_Heap[1] = _Heap[_Size--];
int i = 0;
percolate(1); //从根结点处开始下滑调整顺序
}
void MakeHeap() //置空堆
{
BinaryHeap<T> tmp;
swap(tmp._Heap ,_Heap);
_Size = 0;
}
bool IsEmpty()const //判断堆是不是为空
{
return _Size == 0;
}
const Node& findMin()const //查找堆中的最小元素
{
assert(_Size>0);
return _Heap[1];
}
protected:
void buildHeap() //恢复堆的顺序
{
for (int i =_Size; i > 0; i--)
{
percolate(i);
}
}
void percolate(int hole) //从hole开始下滑调整
{
int child=0;
Node tmp = _Heap[hole];
for (;hole*2<=_Size;hole=child) //如果有左孩子则下滑调整
{
child = hole * 2;
if (child !=_Size&&_Heap[child]> _Heap[child + 1]) //找出左右孩子中值最小的
child++;
if (tmp < _Heap[child]) //如果tmp小于孩子的值,则调整结束
{
break;
}
else //如果tmp大于等于孩子的值,则继续调整
{
_Heap[hole] = _Heap[child];
}
}
_Heap[child] = tmp;
}
protected:
vector<Node> _Heap;
int _Size;
};
//通过仿函数来实现大小堆代码的复用
#pragma once
#include<cassert>
#include<vector>
using namespace std;
template<typename T>
struct Less
{
bool operator()(const T& l,const T& r)
{
return l < r;
}
};
template<typename T>
struct Great
{
bool operator()(const T& l, const T& r)
{
return l>r;
}
};
//通过仿函数,可以建最小堆也可以建最大堆
template<typename T,class Compare=Less<T>>
class Heap
{
public:
Heap()
{}
Heap(T *a, int size)
{
_a.reserve(size);
for (int i = 0; i < size; i++)
{
_a.push_back(a[i]);
}
//建堆
for (int i =(size-2)/2;i>=0; --i) //从最后一个非叶结点开始调整
{
AdjustDown(i,size);
}
}
void Push(const T& x)
{
//插入到尾部,再从最后一个元素开始向上调整
_a.push_back(x);
AdjustUp(_a.size()-1);
}
void Pop()
{
//将堆顶与最后一个元素交换,再从堆顶下滑调整
assert(!_a.empty());
swap(_a[0],_a[_a.size()-1]);
_a.pop_back();
if (_a.size()>1) //如果堆中的元素大于一个,再进行调整
{
AdjustDown(0, _a.size());
}
}
bool Empty()
{
return _a.empty();
}
const T& Top()
{
assert(!_a.empty());
return _a[0];
}
protected:
void AdjustDown(int root,int size) //向下调整算法
{
assert(!_a.empty());
int parent=root;
int child = parent * 2 + 1;
while (child<size)
{
if ((child + 1) < size
&&Compare()(_a[child + 1], _a[child])) //找左右孩子中最大的下标
child++;
if (Compare()(_a[child],_a[parent]))
{
swap(_a[parent],_a[child]);
parent=child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
void AdjustUp(int child) //向上调整算法
{
assert(!_a.empty());
while (child>0)
{
int parent = (child - 1) / 2;
if (Compare()(_a[child],_a[parent]))
{
swap(_a[parent], _a[child]);
child = parent;
}
else
{
break;
}
}
}
private:
vector<T> _a;
};
//优先级队列
#pragma once
#include"heap.h"
template<typename T,class Compare=Less<T> >
class PriQueue
{
public:
void Push(const T& x)
{
h.Push(x);
}
void Pop()
{
h.Pop();
}
const T& Top()
{
return h.Top();
}
private:
Heap<T, Compare> h;
};
//堆排序
#pragma once
#include<cassert>
template<typename T>
struct UpOder
{
bool operator()(const T& l,const T& r) //升序
{
return l < r;
}
};
template<typename T> //降序
struct DownOder
{
bool operator()(const T& l, const T& r)
{
return l>r;
}
};
//默认堆排序是升序,可通过仿函数传递参数设置为降序
template<typename T,class Compare=UpOder<T>>
class HeapSort
{
public:
HeapSort()
{}
void Sort(T* a, int size)
{
//建堆
assert(a);
for (int i = (size - 2) / 2; i >= 0; --i)
{
AdjustDown(a, i, size);
}
//堆排序
while (size >1)
{
swap(a[0],a[size-1]);
--size;
AdjustDown(a,0,size);
}
}
protected:
//下滑调整
void AdjustDown(T* a,int root,int size)
{
assert(size>0);
int parent = root;
int child = parent * 2 + 1;
while (child < size)
{
if ((child + 1) < size&&Compare()(a[child],a[child+1]))
child++;
if (Compare()(a[parent], a[child]))
{
swap(a[parent],a[child]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
};