面试专栏:算法与数据结构,虚拟机,Java基础,JavaWeb
1.二叉树
知识点复习:
二叉树是一棵树,每个节点不能有多于两个的儿子。
二叉查找树的平均深度为O(logN).
节点实现:
class BinaryNode{
Object element;
BinaryNode left;
BinaryNode right;
}
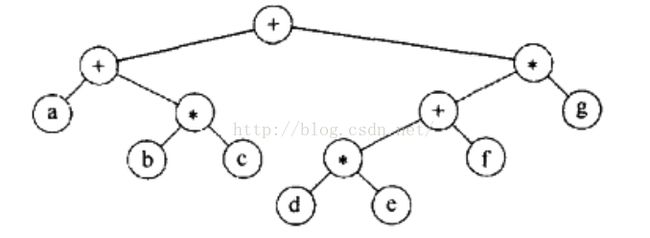
应用:表达式树,如图:
中序遍历:
后序遍历:
先序遍历(不常用):
![]()
后缀表达式转成表达式树的算法:
代码实现(亲测):
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
//知识点:二叉树,栈,内部类,嵌套类,静态域,静态方法,public限定(需增强:输入非法后缀表达式,弹栈易空指针,并且出来的表达式二叉树也非法)
public class OfferTest {
//要被内部static方法使用,必须static
private static class BinaryNode
{
private Object element;//要以对象直接引用,也必须public,但经测试该类外部类方法引用private也合法
public BinaryNode left;
public BinaryNode right;
}
//要以new被外部使用,必须public,但main方法是该外部类内部方法,可以使用private内部类(已测)
private class MyStack
{
private LinkedList<Object> list=new LinkedList<Object>();
public boolean empty(){
return list.size()==0;
}
public void push(Object obj){
list.addFirst(obj);
}
public Object pull(){
if(!empty()){
return list.removeFirst();
}
return null;
}
}
public static BinaryNode toBinaryTree(String input,MyStack stack){//直接引用了内部类名
char[] signs={'+','-','*','/'};
List<Character> list=Arrays.asList('+','-','*','/');
char[] inputs=input.toCharArray();
for(char in:inputs){
if(list.contains(in)){
//经调试:左右元素完全整反了
BinaryNode num1=(BinaryNode)stack.pull();//这应该是操作符右端的元素
BinaryNode num2=(BinaryNode)stack.pull();//这是操作符左端元素
/*BinaryNode node1=new BinaryNode();
node1.element=num1;
BinaryNode node2=new BinaryNode();
node2.element=num2;*/
BinaryNode node3=new BinaryNode();
node3.element=(Character)in;
/*node3.left=node1;
node3.right=node2;*/
node3.left=num2;//后弹出的应该是左元素
node3.right=num1;
stack.push(node3);
}else{
BinaryNode node1=new BinaryNode();
node1.element=(Character)in;
stack.push(node1);
}
}
return (BinaryNode)stack.pull();
}
/**
* 1.求二叉树的最大距离(即相距最远的两个叶子节点),写代码。
*/
public static void binaryTree(){
//复习、应用:
}
public static void main(String[] args)
{
System.out.println("Hello World!");
String input="ab+cde+**";
OfferTest.MyStack stack=new OfferTest().new MyStack();
BinaryNode node=toBinaryTree(input,stack);
System.out.println("OK");
//怎样遍历二叉树打印?怎样求深度,距离?
}
}
调试:
1.弱智的基础问题:Arrays的方法asList写成了toList;静态方法只能使用静态内部类。
2.栈中元素应该全为BinaryNode,第一次因为失误而把栈中取出的BinaryNode又套了一层,成了另一个BinaryNode的element,造成出来的数据结构诡异,幸好仔细调试观察!
3.先入栈的是左元素,结果取出来时是先取右元素,给了树左端,这样整个完全整反了,也已改正测试正确
加:求二叉树的最大距离(即相距最远的两个叶子节点)、遍历算法:
import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
//知识点:二叉树,栈,内部类,嵌套类,静态域,静态方法,public限定(需增强:输入非法后缀表达式,弹栈易空指针,并且出来的表达式二叉树也非法)
public class OfferTest {
//要被内部static方法使用,必须static
private static class BinaryNode
{
private Object element;//要以对象直接引用,也必须public,但经测试该类外部类方法引用private也合法
public BinaryNode left;
public BinaryNode right;
public int leftMaxLength;
public int rightMaxLength;
}
//要以new被外部使用,必须public,但main方法是该外部类内部方法,可以使用private内部类(已测)
private class MyStack
{
private LinkedList<Object> list=new LinkedList<Object>();
public boolean empty(){
return list.size()==0;
}
public void push(Object obj){
list.addFirst(obj);
}
public Object pull(){
if(!empty()){
return list.removeFirst();
}
return null;
}
}
private class MaxLength{
public int maxLen;
}
//private static int df;
public static BinaryNode toBinaryTree(String input,MyStack stack){//直接引用了内部类名
char[] signs={'+','-','*','/'};
List<Character> list=Arrays.asList('+','-','*','/');
char[] inputs=input.toCharArray();
for(char in:inputs){
if(list.contains(in)){
//经调试:左右元素完全整反了
BinaryNode num1=(BinaryNode)stack.pull();//这应该是操作符右端的元素
BinaryNode num2=(BinaryNode)stack.pull();//这是操作符左端元素
/*BinaryNode node1=new BinaryNode();
node1.element=num1;
BinaryNode node2=new BinaryNode();
node2.element=num2;*/
BinaryNode node3=new BinaryNode();
node3.element=(Character)in;
/*node3.left=node1;
node3.right=node2;*/
node3.left=num2;//后弹出的应该是左元素
node3.right=num1;
//No enclosing instance of type OfferTest is
//accessible. Must qualify the allocation with
//an enclosing instance of type OfferTest (e.g. x.new A()
//where x is an instance of OfferTest).
//MaxLength maxLength=new MaxLength();
//如果在外面要用OfferTest.MaxLength类型,但这里的内部类是private,无法在外部使用
//内部类的使用:必须定义在使用前面,而方法则无所谓,编译器的编译顺序决定
MaxLength maxLength=new OfferTest().new MaxLength();
binaryTree(node3,maxLength);
System.out.println(maxLength.maxLen);
stack.push(node3);
}else{
BinaryNode node1=new BinaryNode();
node1.element=(Character)in;
stack.push(node1);
}
}
return (BinaryNode)stack.pull();
}
/**
* 1.求二叉树的最大距离(即相距最远的两个叶子节点),写代码。
*/
public static void binaryTree(BinaryNode root,MaxLength maxLength){
//复习、应用:一切都是从根节点开始,所以各种遍历需要递归实现
/*
int i=0;
if(root==null)
return 0;
else{
//逻辑不对,应该判断左右子树是否为空
//return binaryTree(root.left)+1+binaryTree(root.right)-1;
//return binaryTree(root.left)+binaryTree(root.right);
if(root.left!=null)
i=binaryTree(root.left)+1;
if(root.right!=null)
i=i+binaryTree(root.right)+1;
return i;//特殊情况:如果左右子树都为null而本身不为null,返回0
}
*/
//经测试,上述算法计算的是所有路径总数
//是基准模型建立的不够全面:要判断左子树的左是否为空,和右子树的右是否为空,然后再递归
/*
int i=0;
if(root==null)
return 0;
else{
if(root.left!=null){
if(root.left.left==null)
i=i+1;
//i=1;
else//是else!!不是直接写!!
i=i+1+binaryTree(root.left);
}
if(root.right!=null){
if(root.right.right==null)
i=i+1;
else
i=i+1+binaryTree(root.right);
}
return i;//特殊情况:左右子树皆为null,直接返回0
}
*/
//经测试仍然不对,症结在于:我一递归就把子树的左右子树都加上,这是不对的!!
//实际上非常简单:只要左子树的左边,加1,再加1,再加右子树的右边
//不用递归,一递归就必然加上左右子树的所有,而我们只要左子树的左,右子树的右
/*
int i=0;
if(root==null)
return 0;
else{
BinaryNode left=root.left;
while(left!=null){
i=i+1;
left=left.left;
}
BinaryNode right=root.right;
while(right!=null){
i=i+1;
right=right.right;
}
return i;
}
*/
//以上没验证的东西幼稚可笑到离谱!不知道什么叫做最大距离吗??
//网上答案:以后一切主观臆想都是错的,一切以权威书籍和网上综合成熟的答案为准:
/*
* 分析:递归。最长距离要么经过根节点,要么在左子树或右子树当中,经过左子树或右子树的根节点
* 节点要加上两个存储左右子树最大长度的字段:
* public int leftMaxLength;
* public int rightMaxLength;
*/
if(root==null)
return;
if(root.left==null)
root.leftMaxLength=0;
if(root.right==null)
root.rightMaxLength=0;
//用左或右子树本身的最大长度更新
if(root.left!=null)//递归
binaryTree(root.left,maxLength);//直接调用maxLength这个参数,为了更新其值!
if(root.right!=null)
binaryTree(root.right,maxLength);
//用左和右到根节点最大距离的和更新
if(root.left!=null){
if(root.left.leftMaxLength>root.left.rightMaxLength)
root.leftMaxLength=root.left.leftMaxLength+1;
else
root.leftMaxLength=root.left.rightMaxLength+1;
}
if(root.right!=null){
if(root.right.leftMaxLength>root.right.rightMaxLength)
root.rightMaxLength=root.right.leftMaxLength+1;
else
root.rightMaxLength=root.right.rightMaxLength+1;
}
//最长距离要么经过根节点,要么在左子树或右子树当中,经过左子树或右子树的根节点
//一切诀窍都在这更新上:maxLength必须作为函数参数,因为每次递归都直接调用这个参数更新它
//只要左或右子树为空,对应leftMaxLength就为0,而maxLength是根据它们计算的
//只要左或右子树不为空就更新maxLenth为左或右子树本身的最大距离(递归)
//只要左或右子树距离根节点最大距离哪个大于maxLenth就更新它为左或右子树距离根节点最大距离,而计算出
//最后计算左右子树到根节点最大长度和,如果大于maxLenth也更新它,那么根据一开始的分析,最终它是最大距离!
//注意左右子树的最大长度和左右子树距离根节点的最大长度是两码事!leftMaxLength和left的maxLength不同!
//更新最长距离
if(root.leftMaxLength+root.rightMaxLength>maxLength.maxLen)
maxLength.maxLen=root.leftMaxLength+root.rightMaxLength;
}
/*
* 2.二叉树后序遍历
*/
public static void binaryTreeWalk(BinaryNode root){
if(root==null)
;
else{
//System.out.println(root.left);
binaryTreeWalk(root.left);
//System.out.println(root.right);
binaryTreeWalk(root.right);
System.out.println(root.element);
}
}
/*
* 3.中序变后序:中序怎样表示呢?-->括号也要压栈,弹栈,并处理(优先级)
*/
public static void main(String[] args)
{
System.out.println("Hello World!");
//String input="ab+cde+**";
String input="abc*+de*f+g*+";
OfferTest.MyStack stack=new OfferTest().new MyStack();
BinaryNode node=toBinaryTree(input,stack);
System.out.println("OK");
System.out.println("----------");
MaxLength maxLength=new OfferTest().new MaxLength();
binaryTree(node,maxLength);
//调用上面时,犯了一个最愚蠢的错误
//调试:画树图,肯定此前建立树的正确,打断点,在最初建立的最简单二叉树上进入里层递归
//跟踪末端节点执行递归函数的过程,相关值,从里向外跟踪
//最终发现递归算法是没问题的,里面的maxLength是正确的值而不是都是0的情况
//原来:调用时maxLength是int类型,是值传递,也就是复制,最终函数中改变的maxLength无法传递
//到原来的maxLength上,这样一个算法在最简单的基础上出错,可见基础是多么重要!断点跟踪调试值是多么重要!
//那么这里:定义一个类静态字段也仍然是值传递,定义一个Integer对象也不行
//写一个类吧,包含maxLength字段,程序中修改传入此对象,更新此对象的此字段,这样传入的对象是地址传递了
System.out.println(maxLength.maxLen);
System.out.println("----------");
binaryTreeWalk(node);
//怎样遍历二叉树打印?怎样求深度,距离?
}
}
测试结果:
Hello World!
2
3
2
3
4
7
OK
----------
7
----------
a
b
c
*
+
d
e
*
f
+
g
*
+
2.两个栈实现队列
//import java.util.*;
//两个栈实现一个队列
public class StackSequence
{
//数组实现的栈,或者直接用Java集合中的Stack,待扩展:数组溢出怎样扩展该数组??
private class MyStackArray
{
private Object[] array=new Object[100];
private int i=0;
/*
public boolean empty(){
return i<0;
}
*/
public int lengthOfInnerArray(){
return array.length;
}
public void push(Object obj){//应该判断obj不为null!!
if(i<0)//弹栈到空会让i<0,不修正会发生异常
i=0;
if(i<array.length){
array[i++]=obj;
}//else保留并扩展该数组:待查
}
public Object pull(){
if(i>0){//控制i使其为栈顶,让弹出的元素失效和被覆盖
return array[--i];//!!!是这里的错,压栈后i是栈顶元素索引+1,如果是i--则输出空元素
}
return null;
}
}
//利用两个该栈的对象出入队列
private MyStackArray stack1=new MyStackArray();
private MyStackArray stack2=new MyStackArray();
public void inSequence(Object obj){
//stack1.push(obj);//简单的想法错了,问题是:入栈stack1前,要先弹出stack1底部唯一元素给stack2,这就是要用两个栈实现的原因,而不是一个!!
/*
Object obj1=stack1.pull();
//第一次入栈stack1中并无元素,需要判断:
if(obj1!=null){
stack2.push(obj1);
}
*/
stack1.push(obj);
}
public Object outSequence(){
//stack2不为空,弹栈,问题:stack2中有多个元素,而先入栈的是队列先输入的,应该先出的
//卡壳的地方:应该先把stack1中的元素按出栈顺序入栈stack2
Object obj1=stack2.pull();
if(obj1!=null){
return obj1;
}else{
while((obj1=stack1.pull())!=null){
stack2.push(obj1);
}
return stack2.pull();
}
}
public static void main(String[] args)
{
//测试:栈
StackSequence.MyStackArray stack= new StackSequence().new MyStackArray();
stack.push(new Integer(3));
System.out.println(stack.lengthOfInnerArray());
stack.push(new Integer(5));
System.out.println(stack.lengthOfInnerArray());
stack.push(new Integer(4));
System.out.println(stack.lengthOfInnerArray());
stack.push(new Integer(8));
System.out.println(stack.lengthOfInnerArray());
stack.push(new Integer(9));
stack.push(new Integer(2));
Integer in=(Integer)stack.pull();
while(in!=null){
System.out.println(in);
in=(Integer)stack.pull();
}
System.out.println("----------------");
StackSequence sequence=new StackSequence();
sequence.inSequence(new Character('r'));
sequence.inSequence(new Character('2'));
sequence.inSequence(new Character('x'));
sequence.inSequence(new Character('v'));
sequence.inSequence(new Character('c'));
sequence.inSequence(new Character('p'));
sequence.inSequence(new Character('q'));
sequence.inSequence(new Character('u'));
sequence.inSequence(new Character('y'));
sequence.inSequence(new Character('a'));
Character c=(Character)sequence.outSequence();
while(c!=null){
System.out.println(c);
c=(Character)sequence.outSequence();
}
System.out.println("Hello World!");
}
}
测试结果:
100
100
100
100
2
9
8
4
5
3
----------------
r
2
x
v
c
p
q
u
y
a
Hello World!
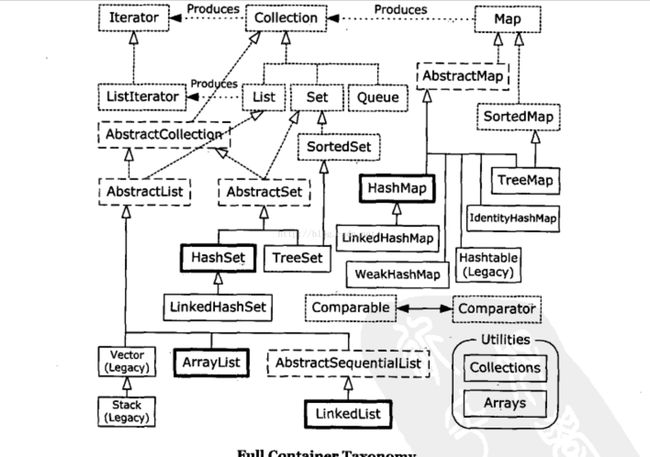
3.Java容器类库深入
完备的体系图(摘自《Java编程思想》):
简单总结:
Collection体系:
以祖先接口Collection下溯,每个子体系一般都会有一个子接口继承祖先接口,一个抽象的实现类实现祖先接口。下边的子孙实现类:是实现这个子接口(图中并没有标出,但已从API继承体系中查到),而继承那个抽象类!有的在中间还有一个接口,间接继承接口;有的在中间还有一个抽象类,间接继承抽象类。
Map体系:
类似于Collection体系,注意仍然有间接的接口继承和间接的抽象类继承,也有直接对祖先接口的实现。注意接口是可以多重继承的,比如ConcurrentNavigableMap继承了两个接口!重点接口和容器:SortedMap,NavigableMap,ConcurrentMap接口;AbstractMap抽象类;TreeMap,ConcurrentHashMap,HashMap实现类。
注意学习的体系:ConcurrentMap体系,多线程相关。
Map体系和Collection体系的关系:(HashSet集合内部实现,HashMap与HashTable)
以下文档摘自Java API
HashSet:
-
public class HashSet<E>- extends AbstractSet<E>
- implements Set<E>, Cloneable, Serializable
此类实现 Set 接口,由哈希表(实际上是一个 HashMap 实例)支持。它不保证 set 的迭代顺序;特别是它不保证该顺序恒久不变。此类允许使用null 元素。
此类为基本操作提供了稳定性能,这些基本操作包括 add、remove、contains 和 size,假定哈希函数将这些元素正确地分布在桶中。对此 set 进行迭代所需的时间与HashSet 实例的大小(元素的数量)和底层HashMap 实例(桶的数量)的“容量”的和成比例。因此,如果迭代性能很重要,则不要将初始容量设置得太高(或将加载因子设置得太低)。
注意,此实现不是同步的。
- 从以下版本开始:
- 1.2
HashMap:
-
public class HashMap<K,V>- extends AbstractMap<K,V>
- implements Map<K,V>, Cloneable, Serializable
基于哈希表的 Map 接口的实现。此实现提供所有可选的映射操作,并允许使用 null 值和null 键。(除了非同步和允许使用 null 之外,HashMap 类与Hashtable 大致相同。)此类不保证映射的顺序,特别是它不保证该顺序恒久不变。
此实现假定哈希函数将元素适当地分布在各桶之间,可为基本操作(get 和 put)提供稳定的性能。迭代 collection 视图所需的时间与HashMap 实例的“容量”(桶的数量)及其大小(键-值映射关系数)成比例。所以,如果迭代性能很重要,则不要将初始容量设置得太高(或将加载因子设置得太低)。
……
- 从以下版本开始:
- 1.2
HashTable:
-
public class Hashtable<K,V>- extends Dictionary<K,V>
- implements Map<K,V>, Cloneable, Serializable
此类实现一个哈希表,该哈希表将键映射到相应的值。任何非 null 对象都可以用作键或值。
为了成功地在哈希表中存储和获取对象,用作键的对象必须实现 hashCode 方法和 equals 方法。
从Java 2 平台 v1.2起,此类就被改进以实现 Map 接口,使它成为 Java Collections Framework 中的一个成员。不像新的 collection 实现,Hashtable 是同步的
- 从以下版本开始:
- JDK1.0
性能与散列实现:
以一个特定标识(可以理解为名称)对象为键,创建同“名”新对象以键查找值的例子:注意必须同时覆盖hashCode()和equals()方法,换成自定义的”相等”,这两个方法都在Object对象当中:
hashCode与散列表数据结构知识补充: