Coursera2014 机器学习第二周 多变量线性回归
多变量线性回归
Linear Regression with multiple variables
week 2 在 week 1 的基础上,将变量扩充到≥2的情况,整体比较简单。
多变量的概念
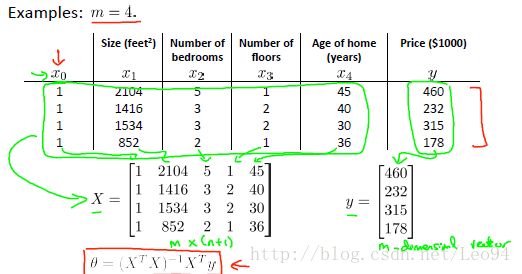
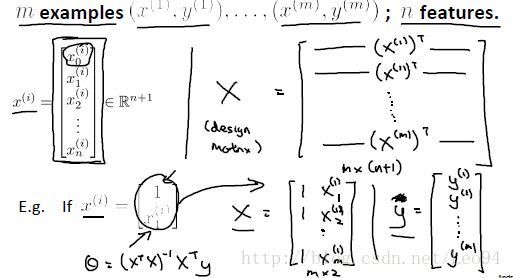
也是一个预测房价的例子,但不同的是,影响房价的因素不止是房子的大小,还引入卧室数量(number of bedrooms),走廊数量(number of floors),房子年龄(years),共4个变量。可以用一个向量的形式来表示训练集中的每个变量(feature)
假设函数可以改写为这样的形式:(因为这里讨论的是线性模型,所以每个变量对结果y的影响都是线性的)
为了表示方便,令x0=1,这样就可以将假设函数h写成矩阵表示的形式
多变量模型的梯度下降法
在week 1的课程中,代价函数可以表示为θ0和θ1的函数形式。多变量模型中,θi的个数增加,这里可以把所有的θ看成一个向量θ,将Week 1的公式写成向量形式。梯度下降法的表示类似,只是θ的个数变多。迭代时同样要注意simultaneously,一定要同时更新所有的θ
变量缩放
为什么要对features做scaling?特征量缩放
每个feature的范围不一样,比如图中这个例子。我们暂时忽略掉θ0的影响,只看θ1和θ2和代价函数J的关系。x1的范围是0~2000,x2的范围是1~5,所以等值线图画出来就会是一个巨大的椭圆,如果x1和x2的范围差距更远的话,每条等值线的距离就会很大,这样收敛的速度会变慢。而接近圆形的等值线图到达中心点(最终converge)的速度很nice。所以要做feature scaling,
将每个变量范围弄到-1~1的范围
(其实也没有必要每个都缩放到-1~1哈,选其他的范围也行,反正不能相差太大。比如-0.000001~0.000001和-100~100)
还有一个办法就是做均值归一化 mean normalization,使变量均值为0。方法就是(xi-u)/s —— s可以是离差max-min,也可以是标准偏差standard deviation
学习速率α
如何选择α的值?
画出代价函数随迭代次数变化的图。可以看出在迭代了300~400次后,代价函数J的值下降得很缓慢,再往后每次迭代可能就变化10^-3这么多,说明J差不多收敛了
下面这三种情况都说明α选得太大,导致代价函数J或一直增大,或变化很大,或来回摇摆,总之就是J不收敛
总结:α太小,收敛慢;α太大,有可能不收敛
在选择α的时候,可以进行尝试。比如从0.001~0.01~0.1~1
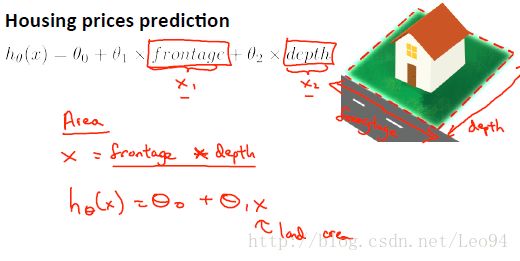
多项式回归(非线性)
我们在做房价预测的时候可能会考虑到frontage、depth以及Aera这几个因素,而面积aera又可以用frontage*depth来表示。所以frontage和depth对房价的影响可以统一用area来表示
然后是
选择回归多项式
。
根据房价的走势,如果选二次的话,随着面积增大,房价反而下降。明显我们不希望是这个结果,所以再加一个三次方的项,这样后面就是一直上升的形式。
也可以选用二次根式来代替平方项
常规方程
除了梯度下降法之外,还可以用常规方程(normal equation)的方法直接解出θ
我们的目标是使代价函数J取最小值,找出此时的参数θ——问题转为求解J的最小值——对J求导=0
假设一共有n个变量features影响房价price(y),m组数据,则矩阵X可表示为
1 x1(1) x2(1) ... xn(1)
. x1(2) x2(2) ... xn(2)
. ... ... ... ...
. ... ... ... ...
1 x1(m) x2(m) ... xn(m)
0~n列,第j列表示第j个变量xj的n个训练数据
1~m行,第i行表示训练集的第i组训练数据
xj(i)表示第i组训练数据中的第j个变量
J(θ)对每一个θj求导之后的导数都应该是0,即J(θj)' = Σ(i=1~m) (h(x(i))-y(i))*xj(i) = 0. 把J(θ)写成向量形式,是为一个行向量J(θ)' = [J(θ1)' J(θ2)' ... J(θn)'] = 0
[J(θ1)' J(θ2)' ... J(θn)'] = ( θT * XT - yT ) * X = 0 —— θ = (XT*X)^(-1)*XT*y
(XT * X)^(-1)是XT*X的逆矩阵,求逆矩阵的方法,Octave中可用pinv()来实现
这种方法可以直接通过矩阵运算求出θ
梯度下降法和常规方程法比较
m组训练数据,n个变量
梯度下降法 常规方程法
需要选择α的取值 不需要选择α
需要很多次迭代 不需要迭代
需要计算(XT*X)^(-1)
适用于n很大的情况 如果n很大 运算会很慢
n在什么情况下算large?——矩阵运算(XT*X)^(-1)的复杂度是O(n^3)。n=100,1000都可以接受,n=10000时,复杂度为10^12,有点悬。当n达到10^6时,计算机真的不行了……还是选用梯度下降法迭代吧
(XT * X)^(-1)是XT*X的逆矩阵,求逆矩阵的方法,Octave中可用pinv()来实现
这种方法可以直接通过矩阵运算求出θ
矩阵XT*X不可逆?non-invertible
面对这种情况,计算机似乎无法进行计算了。
Matlab/Octave中计算逆矩阵有两个命令:inv和pinv。pinv可以计算伪逆(广义逆矩阵)pseudo-inverse,不可逆矩阵也可以用pinv求出逆矩阵,具体可在Matlab中help pinv
当XT*X出现不可逆的情况时,可能因为变量出现冗余,或者说矩阵不满秩(m≤n),所以可以删去一些变量
什么是冗余呢?比如说x1是以feet2为单位的面积变量,x2是以m2为单位的面积变量,这二者之间是线性相关的,x1=x2*3.28,所以这两个变量相当于只有一个,可以删去一个变量,从而防止出现冗余