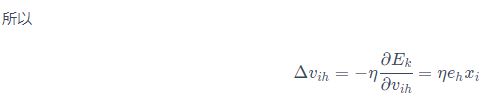《机器学习》周志华西瓜书习题参考答案：第5章 - 神经网络

【机器学习】《机器学习》周志华西瓜书 笔记/习题答案 总目录

• https://blog.csdn.net/TeFuirnever/article/details/96178919

——————————————————————————————————————————————————————

• 【机器学习】《机器学习》周志华西瓜书读书笔记：第5章 - 神经网络

习题

使用线性函数作为激活函数时，无论是在隐藏层还是在输出层（无论传递几层），其单元值（在使用激活函数之前）都还是输入 $x$ 的线性组合，这个时候的神经网络其实等价于逻辑回归（即原书中的对率回归，输出层仍然使用Sigmoid函数）的，若输出层也使用线性函数作为激活函数，那么就等价于线性回归 。

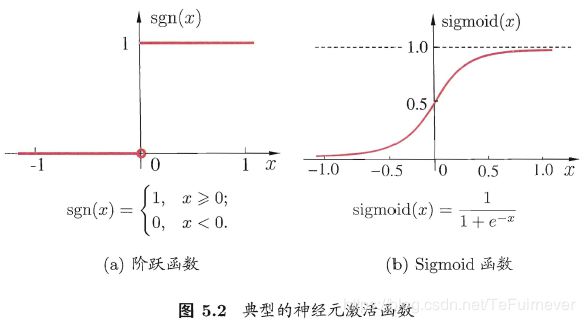
使用Sigmoid激活函数，每个神经元几乎和对率回归相同，只不过对率回归在 $sigmoid(x)>0.5$ 时输出为1，而神经元直接输出 $sigmoid(x)$。

用一张网上找到的图来说明吧。

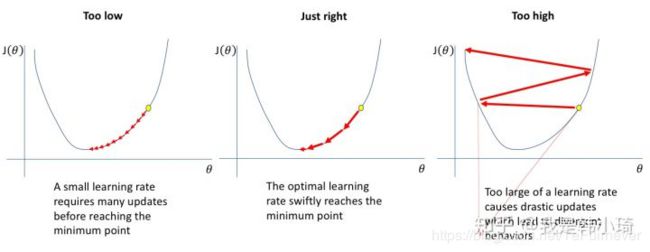
简单说就是学习率太高会导致误差函数来回震荡，无法收敛；而学习率太低则会收敛太慢，影响训练效率，在原书p104也提到过。

学习率 η 控制着梯度下降法的搜索步长（相关内容可参考书p408-附录B.4的梯度下降法的内容）：

从公式去看的话，如下：

对于固定的 η，参考书p109页： η 过大，收敛过程易振荡， η 过小，收敛速度过慢。

常把学习率 η 设置为随迭代次数变化的量，使其随着训练的要求变化而变化（一般是减小）。如刚开始 η 大以快速到达到目标值附近， 后期 η 小以保证收敛稳定。

详细的学习率衰减见博客——【超分辨率】10分钟入门学习率衰减

标准 BP 算法和累积 BP 算法在原书（P105）中也提到过，就是对应标准梯度下降和随机梯度下降，差别就是后者每次迭代用全部数据计算梯度，前者用一个数据计算梯度。

代码在：

import numpy as np
import copy
import pandas as pd
import bpnnUtil
from sklearn import datasets

class BpNN(object):
    def __init__(
            self,
            layer_dims_,
            learning_rate=0.1,
            seed=16,
            initializer='he',
            optimizer='gd'):

        self.layer_dims_ = layer_dims_
        self.learning_rate = learning_rate
        self.seed = seed
        self.initializer = initializer
        self.optimizer = optimizer

    def fit(self, X_, y_, num_epochs=100):
        m, n = X_.shape
        layer_dims_ = copy.deepcopy(self.layer_dims_)
        layer_dims_.insert(0, n)

        if y_.ndim == 1:
            y_ = y_.reshape(-1, 1)

        assert self.initializer in ('he', 'xavier')

        if self.initializer == 'he':
            self.parameters_ = bpnnUtil.xavier_initializer(
                layer_dims_, self.seed)
        elif self.initializer == 'xavier':
            self.parameters_ = bpnnUtil.xavier_initializer(
                layer_dims_, self.seed)

        assert self.optimizer in ('gd', 'sgd', 'adam', 'momentum')
        if self.optimizer == 'gd':
            parameters_, costs = self.optimizer_gd(
                X_, y_, self.parameters_, num_epochs, self.learning_rate)
        elif self.optimizer == 'sgd':
            parameters_, costs = self.optimizer_sgd(
                X_, y_, self.parameters_, num_epochs, self.learning_rate, self.seed)
        elif self.optimizer == 'momentum':
            parameters_, costs = self.optimizer_sgd_monment(
                X_, y_, self.parameters_, beta=0.9, num_epochs=num_epochs, learning_rate=self.learning_rate, seed=self.seed)
        elif self.optimizer == 'adam':
            parameters_, costs = self.optimizer_sgd_adam(X_, y_, self.parameters_, beta1=0.9, beta2=0.999, epsilon=1e-7,
                                                         num_epochs=num_epochs, learning_rate=self.learning_rate,
                                                         seed=self.seed)

        self.parameters_ = parameters_
        self.costs = costs

        return self

    def predict(self, X_):
        if not hasattr(self, "parameters_"):
            raise Exception('you have to fit first before predict.')

        a_last, _ = self.forward_L_layer(X_, self.parameters_)
        if a_last.shape[1] == 1:
            predict_ = np.zeros(a_last.shape)
            predict_[a_last >= 0.5] = 1
        else:
            predict_ = np.argmax(a_last, axis=1)
        return predict_

    def compute_cost(self, y_hat_, y_):
        if y_.ndim == 1:
            y_ = y_.reshape(-1, 1)
        if y_.shape[1] == 1:
            cost = bpnnUtil.cross_entry_sigmoid(y_hat_, y_)
        else:
            cost = bpnnUtil.cross_entry_softmax(y_hat_, y_)
        return cost

    def backward_one_layer(self, da_, cache_, activation_):
        # 在activation_ 为'softmax'时， da_实际上输入是y_， 并不是
        (a_pre_, w_, b_, z_) = cache_
        m = da_.shape[0]

        assert activation_ in ('sigmoid', 'relu', 'softmax')

        if activation_ == 'sigmoid':
            dz_ = bpnnUtil.sigmoid_backward(da_, z_)
        elif activation_ == 'relu':
            dz_ = bpnnUtil.relu_backward(da_, z_)
        else:
            dz_ = bpnnUtil.softmax_backward(da_, z_)

        dw = np.dot(dz_.T, a_pre_) / m
        db = np.sum(dz_, axis=0, keepdims=True) / m
        da_pre = np.dot(dz_, w_)

        assert dw.shape == w_.shape
        assert db.shape == b_.shape
        assert da_pre.shape == a_pre_.shape

        return da_pre, dw, db

    def backward_L_layer(self, a_last, y_, caches):

        grads = {}
        L = len(caches)

        if y_.ndim == 1:
            y_ = y_.reshape(-1, 1)

        if y_.shape[1] == 1:  # 目标值只有一列表示为二分类
            da_last = -(y_ / a_last - (1 - y_) / (1 - a_last))
            da_pre_L_1, dwL_, dbL_ = self.backward_one_layer(
                da_last, caches[L - 1], 'sigmoid')

        else:  # 经过one hot，表示为多分类

            # 在计算softmax的梯度时，可以直接用 dz = a - y可计算出交叉熵损失函数对z的偏导， 所以这里第一个参数输入直接为y_
            da_pre_L_1, dwL_, dbL_ = self.backward_one_layer(
                y_, caches[L - 1], 'softmax')

        grads['da' + str(L)] = da_pre_L_1
        grads['dW' + str(L)] = dwL_
        grads['db' + str(L)] = dbL_

        for i in range(L - 1, 0, -1):
            da_pre_, dw, db = self.backward_one_layer(
                grads['da' + str(i + 1)], caches[i - 1], 'relu')

            grads['da' + str(i)] = da_pre_
            grads['dW' + str(i)] = dw
            grads['db' + str(i)] = db

        return grads

    def forward_one_layer(self, a_pre_, w_, b_, activation_):
        z_ = np.dot(a_pre_, w_.T) + b_
        assert activation_ in ('sigmoid', 'relu', 'softmax')

        if activation_ == 'sigmoid':
            a_ = bpnnUtil.sigmoid(z_)
        elif activation_ == 'relu':
            a_ = bpnnUtil.relu(z_)
        else:
            a_ = bpnnUtil.softmax(z_)

        cache_ = (a_pre_, w_, b_, z_)  # 将向前传播过程中产生的数据保存下来，在向后传播过程计算梯度的时候要用上的。
        return a_, cache_

    def forward_L_layer(self, X_, parameters_):
        L_ = int(len(parameters_) / 2)
        caches = []
        a_ = X_
        for i in range(1, L_):
            w_ = parameters_['W' + str(i)]
            b_ = parameters_['b' + str(i)]
            a_pre_ = a_
            a_, cache_ = self.forward_one_layer(a_pre_, w_, b_, 'relu')
            caches.append(cache_)

        w_last = parameters_['W' + str(L_)]
        b_last = parameters_['b' + str(L_)]

        if w_last.shape[0] == 1:
            a_last, cache_ = self.forward_one_layer(
                a_, w_last, b_last, 'sigmoid')
        else:
            a_last, cache_ = self.forward_one_layer(
                a_, w_last, b_last, 'softmax')

        caches.append(cache_)
        return a_last, caches

    def optimizer_gd(self, X_, y_, parameters_, num_epochs, learning_rate):
        costs = []
        for i in range(num_epochs):
            a_last, caches = self.forward_L_layer(X_, parameters_)
            grads = self.backward_L_layer(a_last, y_, caches)

            parameters_ = bpnnUtil.update_parameters_with_gd(
                parameters_, grads, learning_rate)
            cost = self.compute_cost(a_last, y_)

            costs.append(cost)

        return parameters_, costs

    def optimizer_sgd(
            self,
            X_,
            y_,
            parameters_,
            num_epochs,
            learning_rate,
            seed):
        ''' sgd中，更新参数步骤和gd是一致的，只不过在计算梯度的时候是用一个样本而已。 '''
        np.random.seed(seed)
        costs = []
        m_ = X_.shape[0]
        for _ in range(num_epochs):
            random_index = np.random.randint(0, m_)

            a_last, caches = self.forward_L_layer(
                X_[[random_index], :], parameters_)
            grads = self.backward_L_layer(
                a_last, y_[[random_index], :], caches)

            parameters_ = bpnnUtil.update_parameters_with_sgd(
                parameters_, grads, learning_rate)

            a_last_cost, _ = self.forward_L_layer(X_, parameters_)

            cost = self.compute_cost(a_last_cost, y_)

            costs.append(cost)

        return parameters_, costs

    def optimizer_sgd_monment(
            self,
            X_,
            y_,
            parameters_,
            beta,
            num_epochs,
            learning_rate,
            seed):
        ''' :param X_: :param y_: :param parameters_: 初始化的参数 :param v_: 梯度的指数加权移动平均数 :param beta: 冲量大小， :param num_epochs: :param learning_rate: :param seed: :return: '''
        np.random.seed(seed)
        costs = []
        m_ = X_.shape[0]
        velcoity = bpnnUtil.initialize_velcoity(parameters_)
        for _ in range(num_epochs):
            random_index = np.random.randint(0, m_)

            a_last, caches = self.forward_L_layer(
                X_[[random_index], :], parameters_)
            grads = self.backward_L_layer(
                a_last, y_[[random_index], :], caches)

            parameters_, v_ = bpnnUtil.update_parameters_with_sgd_momentum(
                parameters_, grads, velcoity, beta, learning_rate)
            a_last_cost, _ = self.forward_L_layer(X_, parameters_)
            cost = self.compute_cost(a_last_cost, y_)
            costs.append(cost)

        return parameters_, costs

    def optimizer_sgd_adam(
            self,
            X_,
            y_,
            parameters_,
            beta1,
            beta2,
            epsilon,
            num_epochs,
            learning_rate,
            seed):
        ''' :param X_: :param y_: :param parameters_: 初始化的参数 :param v_: 梯度的指数加权移动平均数 :param beta: 冲量大小， :param num_epochs: :param learning_rate: :param seed: :return: '''
        np.random.seed(seed)
        costs = []
        m_ = X_.shape[0]
        velcoity, square_grad = bpnnUtil.initialize_adam(parameters_)
        for epoch in range(num_epochs):
            random_index = np.random.randint(0, m_)

            a_last, caches = self.forward_L_layer(
                X_[[random_index], :], parameters_)
            grads = self.backward_L_layer(
                a_last, y_[[random_index], :], caches)

            parameters_, velcoity, square_grad = bpnnUtil.update_parameters_with_sgd_adam(
                parameters_, grads, velcoity, square_grad, epoch + 1, learning_rate, beta1, beta2, epsilon)
            a_last_cost, _ = self.forward_L_layer(X_, parameters_)
            cost = self.compute_cost(a_last_cost, y_)
            costs.append(cost)

        return parameters_, costs


if __name__ == '__main__':
    # 5.5
    # data_path = r'C:\Users\hanmi\Documents\xiguabook\watermelon3_0_Ch.csv'
    # data3 = pd.read_csv(data_path, index_col=0)
    # data = pd.get_dummies(data3, columns=['色泽', '根蒂', '敲声', '纹理', '脐部', '触感'])
    # data['好瓜'].replace(['是', '否'], [1, 0], inplace=True)
    # X_test = data.drop('好瓜', axis=1)
    # y_test = data['好瓜']
    #
    # bp = BpNN([3, 1], learning_rate=0.1, optimizer='gd')
    # bp.fit(X_test.values, y_test.values, num_epochs=200)

    # bp1 = BpNN([3, 1], learning_rate=0.1, optimizer='sgd')
    # bp1.fit(X_test.values, y_test.values, num_epochs=200)
    #
    # bpnnUtil.plot_costs([bp.costs, bp1.costs], ['gd_cost', 'sgd_cost'])

    # 5.6
    iris = datasets.load_iris()
    X = pd.DataFrame(iris['data'], columns=iris['feature_names'])
    X = (X - np.mean(X, axis=0)) / np.var(X, axis=0)

    y = pd.Series(iris['target_names'][iris['target']])
    y = pd.get_dummies(y)

    bp = BpNN([3, 3], learning_rate=0.003, optimizer='adam')
    bp.fit(X.values, y.values, num_epochs=2000)

    bp1 = BpNN([3, 3], learning_rate=0.003, optimizer='sgd')
    bp1.fit(X.values, y.values, num_epochs=2000)

    bpnnUtil.plot_costs([bp.costs, bp1.costs], ['adam_cost', 'sgd_cost'])

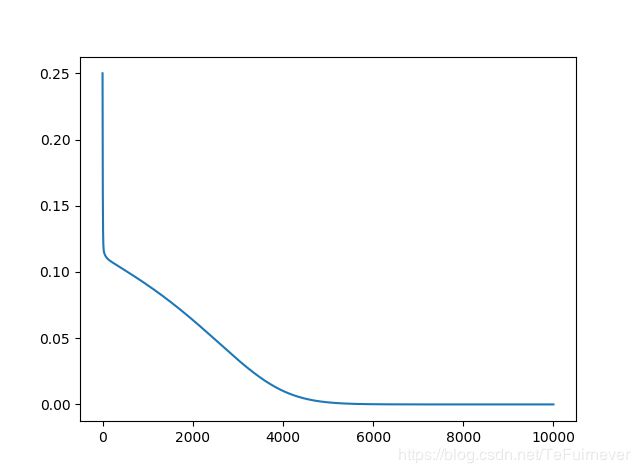
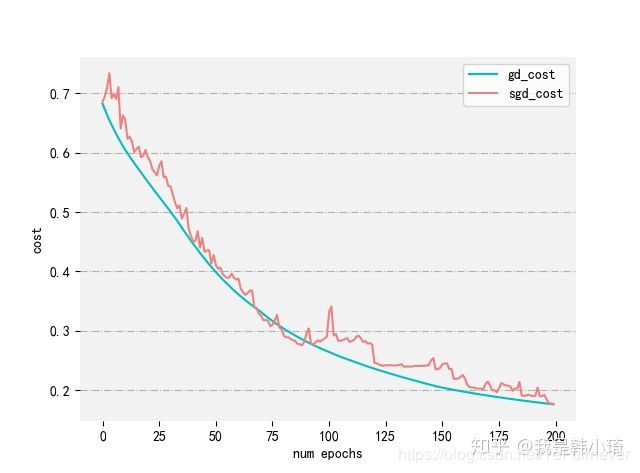
具体两种情况的结果如下图：可以看出来gd的成本函数收敛过程更加稳定，而sgd每次迭代并不一定向最优方向前进，但总体方向是收敛的，且同样是迭代200次，最后结果相差不大，但由于sgd每次迭代只使用一个样本，计算量大幅度下降，显然sgd的速度会更快。

ps.关于随机梯度下降的实现，好像有两种方式，一种是每次将样本打乱，然后遍历所有样本，而后再次打乱、遍历；另一种是每次迭代随机抽取样本。这里采取的是后一种方式，貌似两种方式都可以。

此外，BP神经网络代码在以前学吴恩达老师深度学习课程的时候就写过，这次整理了一下正好放上来，所以很多代码和课程代码类似，添加了应用多分类的情况的代码。下面的5.6题也一并在这里实现。

动态调整学习率有很多现成的算法，RMSProp、Adam、NAdam等等。也可以手动实现一个简单指数式衰减 ，$r$ 是一个超参。这里代码实现了Adam，代码和5.5一同实现，在上面。

这里只尝试了sklearn 中自带的iris数据集试了一下。同样学习率下，两者训练时损失函数如下：

可以明显看出adam的速度更快的。

这里可以使用X = array([[1, 0], [0, 1], [0, 0], [1, 1]])，y = array([[1], [1], [0], [0]])作为数据，训练一个RBF神经网络。

这里使用均方根误差作为损失函数；输出层和书上一致，为隐藏层的线性组合，且另外加上了一个偏置项（这是书上没有）。

代码在：

''' 这里使用均方根误差作为损失函数的RBF神经网络。 '''
import numpy as np
import matplotlib.pyplot as plt

def RBF_forward(X_, parameters_):
    m, n = X_.shape
    beta = parameters_['beta']
    W = parameters_['W']
    c = parameters_['c']
    b = parameters_['b']

    t_ = c.shape[0]
    p = np.zeros((m, t_))  # 中间隐藏层的激活值 对应书上5.19式
    x_c = np.zeros((m, t_))  # 5.19式中 x - c_{i}
    for i in range(t_):
        x_c[:, i] = np.linalg.norm(X_ - c[[i], ], axis=1) ** 2

        p[:, i] = np.exp(-beta[0, i] * x_c[:, i])

    a = np.dot(p, W.T) + b
    return a, p, x_c

def RBF_backward(a_, y_, x_c, p_, parameters_):
    m, n = a_.shape
    grad = {}
    beta = parameters_['beta']
    W = parameters_['W']

    da = (a_ - y_)      # 损失函数对输出层的偏导 ，这里的a其实对应着 输出层的y_hat

    dw = np.dot(da.T, p_) / m
    db = np.sum(da, axis=0, keepdims=True) / m
    dp = np.dot(da, W)   # dp即损失函数对隐藏层激活值的偏导

    dbeta = np.sum(dp * p_ * (-x_c), axis=0, keepdims=True) / m

    assert dbeta.shape == beta.shape
    assert dw.shape == W.shape
    grad['dw'] = dw
    grad['dbeta'] = dbeta
    grad['db'] = db

    return grad

def compute_cost(y_hat_, y_):
    m = y_.shape[0]
    loss = np.sum((y_hat_ - y) ** 2) / (2 * m)
    return np.squeeze(loss)

def RBF_model(X_, y_, learning_rate, num_epochs, t):
    ''' :param X_: :param y_: :param learning_rate: 学习率 :param num_epochs: 迭代次数 :param t: 隐藏层节点数量 :return: '''
    parameters = {}
    np.random.seed(16)
    # 定义中心点，本来这里的中心点应该由随机采用或者聚类等非监督学习来获得的，这里为了简单就直接定义好了

    parameters['beta'] = np.random.randn(1, t)  # 初始化径向基的方差
    parameters['W'] = np.zeros((1, t))  # 初始化
    parameters['c'] = np.random.rand(t, 2)
    parameters['b'] = np.zeros([1, 1])
    costs = []

    for i in range(num_epochs):
        a, p, x_c = RBF_forward(X_, parameters)
        cost = compute_cost(a, y_)
        costs.append(cost)
        grad = RBF_backward(a, y_, x_c, p, parameters)

        parameters['beta'] -= learning_rate * grad['dbeta']
        parameters['W'] -= learning_rate * grad['dw']
        parameters['b'] -= learning_rate * grad['db']

    return parameters, costs

def predict(X_, parameters_):
    a, p, x_c = RBF_forward(X_, parameters_)

    return a

X = np.array([[1, 0], [0, 1], [0, 0], [1, 1]])
y = np.array([[1], [1], [0], [0]])
#

parameters, costs = RBF_model(X, y, 0.003, 10000, 8)

plt.plot(costs)
plt.show()

print(predict(X, parameters))

# 梯度检验
# parameters = {}
# parameters['beta'] = np.random.randn(1, 2) # 初始化径向基的方差
# parameters['W'] = np.random.randn(1, 2) # 初始化
# parameters['c'] = np.array([[0.1, 0.1], [0.8, 0.8]])
# parameters['b'] = np.zeros([1, 1])
# a, p, x_c = RBF_forward(X, parameters)
#
# cost = compute_cost(a, y)
# grad = RBF_backward(a, y, x_c, p, parameters)
#
#
# parameters['b'][0, 0] += 1e-6
#
# a1, p1, x_c1 = RBF_forward(X, parameters)
# cost1 = compute_cost(a1, y)
# print(grad['db'])
#
# print((cost1 - cost) / 1e-6)

最后输出是：

[[ 9.99944968e-01]
 [ 9.99881045e-01]
 [ 8.72381056e-05]
 [ 1.26478454e-04]]

感觉分类的时候在输出层使用sigmoid作为激活函数也可以。

周志华《机器学习》课后习题解答系列（六）：Ch5.8 - SOM网络实验

Elman 网络在西瓜书原书上说的是“递归神经网络”，但是在网上找资料说的

• “递归神经网络”是空间维度的展开，是一个树结构。
• “循环神经网络”是时间维度的展开，代表信息在时间维度从前往后的的传递和积累。

从书上p111描述来看感觉更像“循环神经网络”。最近时间不多（lan…），就不去啃原论文了。关于“循环神经网络”或者递归神经网络的BP可以参考下面链接。

1、零基础入门深度学习(5) - 循环神经网络 ，网上大神写了。

另外关于循环神经网络也可以看看吴恩达老师的深度学习课程“序列模型”那部分。

正好前段时间做过Kaggle上手写数字识别的题目。这里正好放上来，CNN是用Tensorflow实现的，之前看吴恩达老师深度学习课程的时候也拿numpy实现过（课程作业），等以后有时间再整理放上来吧。

https://github.com/han1057578619/kaggle_competition/tree/master/Digit_Recogniz

参考文章

• 机器学习（周志华）课后习题
• https://blog.csdn.net/snoopy_yuan/article/category/6788615