十大经典排序算法(Python语言描述)
本文主要参考下面这篇博客,感觉讲的很好。
https://www.cnblogs.com/onepixel/articles/7674659.html
记录这篇博客,一是想检验一下自己的学习效果,二是刚好借此机会锻炼一下自己Python编程能力。
下面就言归正传啦
目录
- 冒泡排序
- 选择排序
- 插入排序
- 希尔排序
- 归并排序
- 快速排序
- 堆排序
- 计数排序
- 桶排序
- 基数排序
1 冒泡排序
1.1 算法描述
依次比较相邻的元素,如果前一个元素比后一个元素大,则交换两个元素的位置;
这样每一轮循环,可以将本轮循环中的最大元素移到本轮的最后。
优化:
在一轮循环中,如果没有发生位置交换,则此时序列已经排序结束。
1.2 代码实现
def bubbleSort(arr):
l = len(arr)
for i in range(l):
flag = False
for j in range(l-i-1):
if arr[j] > arr[j+1]:
arr[j],arr[j+1] = arr[j+1],arr[j]
flag = True
if flag == False:
break
return arr
print(bubbleSort([5,5,5,2,3,8,1]))
1.3 算法分析
时间复杂度:优化后最好 O ( n ) O(n) O(n),最坏 O ( n 2 ) O(n^2) O(n2),平均情况 O ( n 2 ) O(n^2) O(n2)
2 选择排序
2.1 算法描述
初始状态,有序区为:[ ],无序区为arr[ : ]
第i(i=0,1,2,…,n-2)次排序,当前有序区为arr[:i],无序区为arr[i:],从无序区选择一个最小的元素,将其放在下标为i的位置,即将最小的元素与当前位置i的元素交换。
2.2 代码实现
def select_sort(arr):
l = len(arr)
for i in range(l - 1):
min_index = i
for j in range(i + 1, l):
if arr[j] < arr[min_index]:
min_index = j
arr[i], arr[min_index] = arr[min_index], arr[i]
return arr
print(select_sort([5,5,5,2,3,8,1]))
2.3 算法分析
时间复杂度: O ( n 2 ) O(n^2) O(n2)
3 插入排序
3.1 算法描述
通过构建有序序列,对未排序的数据,在已排序序列中从后向前扫描, 记当前位置为temp, 若扫描位的元素比temp大,则将该元素后移以为,直到找到比temp小的元素为止,把temp插入到该元素的后一位。
##3.2 代码实现
def insert_sort(arr):
l = len(arr)
for i in range(1, l):
j = i-1
temp = arr[i]
while j >= 0 and arr[j] > temp:
arr[j+1] = arr[j]
j -= 1
arr[j+1] = temp
return arr
print(insert_sort([5,5,5,2,3,8,1]))
3.3 算法分析
时间复杂度:最佳情况: O ( n ) O(n) O(n);最坏情况: O ( n 2 ) O(n^2) O(n2);平均时间复杂度: O ( n 2 ) O(n^2) O(n2)
4 希尔排序
4.1 算法描述
希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;
过程演示如下:
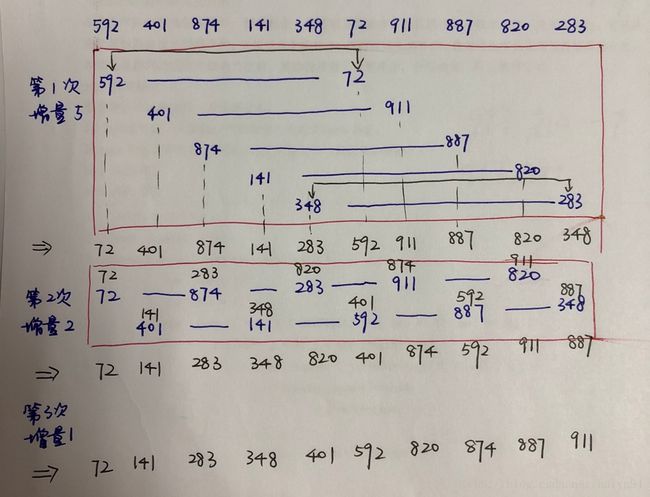
4.2 代码实现
def shell_sort(arr):
count = len(arr)
step = 2
group = count // step
while group > 0:
for i in range(group):
j = i + group
while j < count:
key = arr[j]
k = j - group
while k >= 0 and arr[k] > key:
arr[k + group] = arr[k]
k -= group
arr[k+group] = key
j += group
group //= step
return arr
4.3 算法分析
时间复杂度: 最佳情况: O ( n ) O(n) O(n),最坏情况: O ( n 2 ) O(n^2) O(n2),平均情况: O ( n ( 1.3 ) ) O(n^(1.3)) O(n(1.3))
5 归并排序
5.1 算法描述
把长度为n的输入序列分成两个长度为 n 2 \frac{n}{2} 2n的子序列;
对着两个子序列分别采用归并排序;
将两个排序好的子序列合并成一个最终的排序序列。
5.2 代码实现
def merge(left, right):
i, j = 0, 0
res = []
while i < len(left) and j < len(right):
if left[i] <= right[j]:
res.append(left[i])
i += 1
else:
res.append(right[j])
j += 1
res += left[i:]
res += right[j:]
return res
def merge_sort(arr):
if len(arr) <= 1:
return arr
num = len(arr) // 2
left = merge_sort(arr[:num])
right = merge_sort(arr[num:])
return merge(left, right)
print(merge_sort([5,5,5,2,3,8,1]))
5.3 算法分析
时间复杂度: 最佳情况: O ( n l o g n ) O(nlogn) O(nlogn),最坏情况: O ( n l o g n ) O(nlogn) O(nlogn),平均情况: O ( n l o g n ) O(nlogn) O(nlogn)
6 快速排序
6.1 算法描述
从数列中挑出一个元素,称为基准;
重新排列数列,所有元素比基准小的摆放在基准前面,所有元素比基准大的摆在基准后面;
在这个分区结束之后,该基准就位于数列的中间位置;
递归地对基准左右两边的数列进行排序。
6.2 代码实现
def quick_sort(arr):
def solve(arr, left, right):
if left >= right:
return arr
key = arr[left]
low = left
high = right
while left < right:
while left < right and arr[right] >= key:
right -= 1
arr[left] = arr[right]
while left < right and arr[left] <= key:
left += 1
arr[right] = arr[left]
arr[right] = key
solve(arr, low, left - 1)
solve(arr, left+1, high)
return arr
return solve(arr, 0, len(arr)- 1)
print(quick_sort([5,5,5,2,3,8,1]))
6.3 算法分析
时间复杂度: 最佳情况: O ( n l o g n ) O(nlogn) O(nlogn),最坏情况: O ( n 2 ) O(n^2) O(n2),平均情况: O ( n l o g n ) O(nlogn) O(nlogn)
7 堆排序
7.1 算法描述
利用堆数据结构所设计的一种排序算法,通过每次弹出堆顶元素实现排序。
7.2 代码实现
import heapq
def heap_sort(arr):
heapq.heapify(arr)
res = []
while arr:
res.append(heapq.heappop(arr))
return res
print(heap_sort([5,5,5,2,3,8,1]))
7.3 算法分析
时间复杂度: 最佳情况: O ( n l o g n ) O(nlogn) O(nlogn),最坏情况: O ( n l o g n ) O(nlogn) O(nlogn),平均情况: O ( n l o g n ) O(nlogn) O(nlogn)
8 计数排序
8.1 算法描述
核心思想:将输入数据值转化为键存储在额外开辟的数组空间中。
找出待排序数组中的最大元素,建立该长度的数组c;
统计数组中每个值为i的元素出现的次数;
对所有计数累加,表示该元素位于有序表中第几项;
反向填充目标数组:将每个元素i放在新数组的第c[i]项,每放一个元素就将c[i]-1
8.2 代码实现
def count_sort(arr):
res = [None for i in range(len(arr))]
max_arr = max(arr)
c = [0 for i in range(max_arr + 1)]
for a in arr:
c[a] += 1
for i in range(1, max_arr+1):
c[i] += c[i-1]
for i in range(len(arr)-1, -1, -1):
res[c[arr[i]] - 1] = arr[i]
c[arr[i]] -= 1
return res
print(count_sort([5,5,5,2,3,8,1]))
8.3 算法分析
当输入元素是n个0-k之间的整数是,它的运行时间是 O ( n + k ) O(n+k) O(n+k)
9 桶排序
##9.1 算法描述
假设输入数据服从均匀分布,将数据分到有限数量的桶里,每个桶再分别排序。
设定一个定量长度的数组当空桶;
遍历输入数据,并且吧数据一个一个放到对应的桶中;
对每个不是空的桶进行排序;
从不是空的桶里把排好序的数据拼接起来。
9.2 代码实现
def bucket_sort(arr):
pre_lst = [0]*max(arr)
res = []
for a in arr:
pre_lst[a-1] += 1
i = 0
while i < len(pre_lst):
j = 0
while j < pre_lst[i]:
res.append(i+1)
j += 1
i += 1
return res
print(bucket_sort([5,5,5,2,3,8,1]))
上述代码中假设每个桶的大小为1
9.3 算法分析
k为桶的个数
时间复杂度:最佳情况: O ( n + k ) O(n+k) O(n+k),最坏情况: O ( n 2 ) O(n^2) O(n2),平均情况: O ( n + k ) O(n+k) O(n+k)
10 基数排序
10.1 算法描述
对每一位进行排序,从最低位开始,直到最高位。
取得数组中的最大数,并取得维数;
arr为原始数组,从最低位开始去没给我位组成radix数组;
对radix进行计数排序
10.2 代码实现
def radix_sort(arr):
max_arr = max(arr)
d = len(str(max_arr))
for k in range(d):
s = [[] for i in range(10)]
for i in arr:
s[i//(10**k)%10].append(i)
arr = [j for i in s for j in i]
return arr
print(radix_sort([5,5,5,2,3,8,1]))
10.3 算法分析
时间复杂度:最佳情况: O ( n ∗ k ) O(n*k) O(n∗k),最坏情况: O ( n ∗ k ) O(n*k) O(n∗k),平均情况: O ( n ∗ k ) O(n*k) O(n∗k)