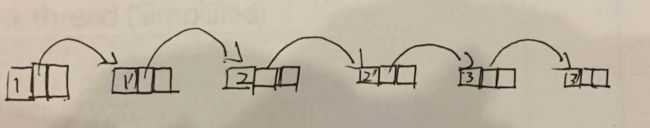刷题代码库及一些犯过错误
本文章仅作代码记录之用。
1、前序遍历二叉树
Pre-order Traversal Binary Tree
方法1:递归(Recursive)
public class Solution {
/**
* @param root: The root of binary tree.
* @return: Preorder in ArrayList which contains node values.
*/
private void traversalTree(TreeNode input, ArrayList output){
if(input == null){
return;
}
output.add(input.val);
if(input.left != null){
traversalTree(input.left,output);
}
if(input.right != null){
traversalTree(input.right,output);
}
return;
}
public ArrayList preorderTraversal(TreeNode root) {
// write your code here
ArrayList return_list = new ArrayList();
traversalTree(root,return_list);
return return_list;
}
} 方法2:分治(Divide and Conquer)
public class Solution {
/**
* @param root: The root of binary tree.
* @return: Preorder in ArrayList which contains node values.
*/
public ArrayList preorderTraversal(TreeNode root) {
// write your code here
ArrayList return_list = new ArrayList();
if(root == null){
return return_list;// mistake1
}
ArrayList temp1 = preorderTraversal(root.left);
ArrayList temp2 = preorderTraversal(root.right);
return_list.add(root.val);//mistake3
return_list.addAll(temp1);//mistake2
return_list.addAll(temp2);
return return_list;
}
} mistake1:如果声明了返回类型的方法,一个要返回相应的类型,不能只是return;
mistake2: 如果一个arraylist添加另一个arraylist,需要用的函数是addAll();
mistake3: 注意TreeNode是一个类,而我们需要添加的是它的值。
2016年12月7日,非递归版本:
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
public class Solution {
//non-recursive version
public List preorderTraversal(TreeNode root) {
List return_list = new ArrayList();
if(root == null){
return return_list;
}
LinkedList stack = new LinkedList();
stack.addLast(root);
while(!(stack.isEmpty())){
TreeNode tmp = stack.removeLast();
return_list.add(tmp.val);
if(tmp.right != null){
stack.add(tmp.right);
}
if(tmp.left != null){
stack.add(tmp.left);
}
}
return return_list;
}
} 2、求二叉树的最长深度
1)递归遍历的方法(最暴力、直接)
将走到的所有点的深度记录下来,直接求最大可得结果。在这题当中思考过,递归中传输进参数的必须是自定义类才能把方法中的改变传出来。所以,试过Integer,发现Integer不能重定义,我们需要改变指向的对象的val,但是intValue只能获取value,并不能改变。同时,integer + 1也没用,因为又创建了新的引用指向新的对象。所以,如果想改变的基本类型,最好还是创建一个新的自定义类。
public class Solution {
/**
* @param root: The root of binary tree.
* @return: An integer.
*/
private void traversal(TreeNode input, ArrayList depth_list, int depth){
if(input == null){
return;
}
int new_depth = depth + 1;
depth_list.add(new_depth);
traversal(input.left,depth_list,new_depth);
traversal(input.right,depth_list,new_depth);
}
public int maxDepth(TreeNode root) {
// write your code here
int init_depth = 0;
ArrayList depth_list = new ArrayList();
depth_list.add(init_depth);
traversal(root,depth_list,init_depth);
return Collections.max(depth_list).intValue();
}
} 需要思考好最极端最小的情况返回什么,返回之后倒数第二层怎么处理最极端的返回值。其实,一个headsup就是,分治只是把问题处理的数据分小了,问题还是不变的。所以这里的处理方法还是Math.max(两个返回值)。
public class Solution {
/**
* @param root: The root of binary tree.
* @return: An integer.
*/
// private static depth = 0;
public int maxDepth(TreeNode root) {
// write your code here
if(root == null){//why this is the termination? because you don't need to consider the left and right children
return 0;
}
int temp1 = maxDepth(root.left);
int temp2 = maxDepth(root.right);
return 1+Math.max(temp1,temp2);
}
}3、判断一棵二叉树是否是平衡二叉树
这个问题不能太过于一蹴而就,很容易产生的想法是直接用上面的求最大深度的代码求得根节点左右字数的最大深度,相减看绝对是否小于等于1。殊不知,判断平衡二叉树的充分条件是最大深度减最少深度的差的绝对值。而且还要相互减,做两次实验,如果两次都小于等于1,才是平衡二叉树。所以比较麻烦。
所以,一个简单的方法是改一下上面的最大深度函数,改成返回是、非的函数。
思路体现了解决问题的步骤:1)左子树是不是平衡二叉树?不是,直接不是。2)右子树是不是?3)如果左右都是了,目前两者的长度是不是相差1以内?
如果一直是的话,保持返回长度值供上一层的运算,否则返回-1,省去上一次的运算。
public class Solution {
/**
* @param root: The root of binary tree.
* @return: True if this Binary tree is Balanced, or false.
*/
private int maxDepth(TreeNode input){
if(input == null){
return 0;
}
int temp1 = maxDepth(input.left);
int temp2 = maxDepth(input.right);
if(temp1 == -1 || temp2 == -1 || Math.abs(temp1-temp2)>1)
return -1;
else{
return 1+Math.max(temp1,temp2);
}
}
public boolean isBalanced(TreeNode root) {
// write your code here
return maxDepth(root) != -1;
}
}当然,也可以使用最简单暴力的遍历的方法:
利用的思想是如果一个节点有一个子节点为空,而它的另外一棵子树一旦大于等于2时,则肯定不会是平衡二叉树。
public class Solution {
/**
* @param root: The root of binary tree.
* @return: True if this Binary tree is Balanced, or false.
*/
private void traversal(TreeNode input,HashMap output, int depth){
if(input==null){
return;
}
depth = depth +1;
if(output.get(depth)==null){
output.put(depth,1);
}else{
output.put(depth,output.get(depth).intValue() + 1);
}
traversal(input.left,output,depth);
traversal(input.right,output,depth);
}
public boolean isBalanced(TreeNode root) {
// write your code here
if(root == null){
return true;
}
int depth = 0;
HashMap record = new HashMap();
traversal(root,record,depth);
for(Integer i : record.keySet()){
if(record.get(i) != Math.pow(2,i-1)){// mistake1
if(record.get(i+1) != null){
return false;
}
}
}
return true;
}
} 这个方法利用了一个满二叉树在某一个深度i的那层,应该有2^(i-1)个元素。如果某个深度不是完整的,而又具有下一层,则存在高度差大于1的情况。不是平衡二叉树。注意,^是位运算的‘与’。x^n的表示为Math.pow(x,n).
4、数字三角形,类树型数组题:
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
最简单直接的办法:遍历每个路径(方案),遇到比当前最好的方案更好的方案时,更新当前最优方案的sum。
代码:
public class Solution {
private void traversal(int sum, int row, int col, List> triangle){
if(row == depth-1){
sum+= triangle.get(row).get(col);
if(sum < best){
best = sum;
}
return;
}
traversal(sum+triangle.get(row).get(col),row+1,col,triangle);
traversal(sum+triangle.get(row).get(col),row+1,col+1,triangle);
return;
}
private int best = 2147483647;
private int depth = 0;
public int minimumTotal(List> triangle) {
depth = triangle.size();
traversal(0,0,0,triangle);
return best;
}
} 采用分治的方法:
public class Solution {
private int miniSum(List> triangle, int row, int col){
if(row == depth-1){
return triangle.get(row).get(col);
}
int left = miniSum(triangle, row+1, col);
int right = miniSum(triangle,row+1,col+1);
return triangle.get(row).get(col)+Math.min(left,right);
}
private int depth;
public int minimumTotal(List> triangle) {
this.depth = triangle.size();
return miniSum(triangle,0,0);
}
} 分治的思想就是用子问题的累积当前问题的最优。
复杂度分析:这个程序同样是每个路径都需要走一遍。所以复杂度仍然是:O(2^n). n为高度。
仔细分析上述程序,发现其采用的遍历和分治都是把这个数字三角形当作二叉树来处理。前述分析过,二叉树的递归遍历和分治遍历的复杂度都是和二叉树的节点数N的关系是O(N)。当一颗二叉树是完全二叉树时,复杂度就是O(2^n)。然而,这个数字三角形的节点个数和当前高度n的关系是:(n-1)^2+n,是n^2的关系。那么,怎么样能使每个节点都只被计算(执行)一次呢?使得复杂度降为:O(n^2)呢?
这就涉及到记忆化搜索的问题,把所有点的最优结果存下来,当再次走到这个点时,可以直接引用这个点的结果。这样,每个点就可以只被计算一次,使得复杂度变为O(n^2)。
public class Solution {
private int miniSum(List> triangle, int row, int col, ArrayList> ans){
if(row == depth-1){
return triangle.get(row).get(col);
}
if(col < ans.get(row).size() && ans.get(row).get(col) != null){
return ans.get(row).get(col);
}
int left = miniSum(triangle, row+1, col,ans);
int right = miniSum(triangle,row+1,col+1,ans);
int best = triangle.get(row).get(col)+Math.min(left,right);
ans.get(row).add(best);
return best;
}
private int depth;
public int minimumTotal(List> triangle) {
ArrayList> ans = new ArrayList>();
this.depth = triangle.size();
for(int i=0;i());
}
return miniSum(triangle,0,0,ans);
}
} 这道题写的时候有些坑 踩到了:
1/ 注意Collection的容量和size()是两回事。容量只是为了将来减少因容量增长而向新数组复制内容的次数。
引用内容(来源:http://wiki.jikexueyuan.com/project/java-collection/arraylist.html):
每个 ArrayList 实例都有一个容量,该容量是指用来存储列表元素的数组的大小。它总是至少等于列表的大小。随着向 ArrayList 中不断添加元素,其容量也自动增长。自动增长会带来数据向新数组的重新拷贝,因此,如果可预知数据量的多少,可在构造 ArrayList 时指定其容量。在添加大量元素前,应用程序也可以使用 ensureCapacity 操作来增加 ArrayList 实例的容量,这可以减少递增式再分配的数量。
而size()则是返回当前容器内元素的数目。即使你初始化了一个10容量的容器,size()还是0的。
而所有的add/ set和get以及remove都会看你输入的index是否
2/ 短路与的作用在这道题就体现出来了:当判断了col < ans.get(row).size()之后,如果满足了前一点,才会继续执行后面的判断。否则,有可能会抛出异常使程序终止。
其实,上述程序就是动态规划思想和普通的分治之间的不同。分治的思想是把问题分到最小块,通过不断地积累局部最优,最后达到全局最优。而动态规划的不仅仅需要有远视的功能(通过分治提供几个局部最优),更是在于消除了重复的计算。(这里顺便提一句所谓的贪心算法,只是根据局部值判断走向,非局部最优值,根据当前利益判断而非长久利益)
动态规划在于在执行每步的计算后,把当前计算结果存储下来,即可供下一步的存在多个计算复用。以消除重复计算。
所以,上面的题目也可以通过循环做(一般动态规划的题,最好通过循环做):
public class Solution {
public int minimumTotal(List> triangle) {
if(triangle == null){
return 0;
}
/*Initilize the status arrays, a medium to store the status*/
//类似于分治,先处理最小的最优情况,最后积累到起点(整体)
int[][] status = new int[triangle.size()][triangle.size()];// 第i行,有i个元素,往上的话,空着的留着是0就好
//初始化最后一行的状态(最小状态)
for(int i=0; i=0; i--){
for(int j=0;j<=i;j++){
status[i][j] = triangle.get(i).get(j) + Math.min(status[i+1][j],status[i+1][j+1]);
}
}
return status[0][0];
}} 当然,动态规划也有纯存储计算结果,到最后再得到最优解的方式:就是自顶向下的方式
public class Solution {
public int minimumTotal(List> triangle) {
if(triangle == null){
return 0;
}
int[][] status = new int[triangle.size()][triangle.size()];
/*通过第一行初始化状态数组*/
status[0][0] = triangle.get(0).get(0);
for(int i=1; ii-1){
status[i][j] = status[i-1][j-1] + triangle.get(i).get(j);
continue;
}
status[i][j] = Math.min(status[i-1][j-1],status[i-1][j]) + triangle.get(i).get(j);
}
}
int ans = 2147483647;//MAXINT
for(int i=0; i 上述的方法中,自底向上的算法比自顶向下的方法要好。效率更高。
其实,这道数字三角形的题目,只是矩阵型动态规划的一个例子。它就相当于是一个矩阵沿着反对角线被分成两半。
下面来简单说一下,我所理解的动态规划思想。
当需要解决的当前问题可以分解为两个或者多个(通常是两个)子问题,然后子问题也可以分成更小的子问题,直到分到某个子问题可以从已知条件解决。然后,通过动态规划的核心——状态矩阵,再逐渐往上构成当前问题的答案。
这其实类似于二叉树的分治方法,只不过,通过分治的词都与二叉树有关系。在二叉树的情况下,子问题就是子树的问题,而对应在矩阵当中,不复存在这种子树和父节点的关系。所以,子问题就是往起点方向走的问题。
所以,在二叉树当中,最小的子问题情况是叶子节点。而在矩阵问题中,最小的子问题是起点和第一列、第一行(可以根据起点和数据在一开始就初始化的)。
一般而言,二叉树型的动态规划比较适合用自底向上,而矩阵型的适合自顶向下。这是由子问题的方向不同而言。
通过,存储小的子问题的计算结果(状态矩阵),可以消除更大的问题时的重复计算。(从上面数字三角形的题可知)。下面在写几道矩阵型动态规划的题目:
/****************************动态规划部分****************************/
5、Minimum Path Sum(最大最小问题)
Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path.
Note: You can only move either down or right at any point in time.
public class Solution {
public int minPathSum(int[][] grid) {
if(grid == null || grid[0] == null){
return 0;
}
//initialize
int row = grid.length;
int col = grid[0].length;
int[][] status = new int[row][col];
//trick, initialize basic situations
status[0][0] = grid[0][0];
for(int i=1;i矩阵型动态规划的技巧是:对于状态第0行或者第0列的数据,往往可以根据现有的数据直接得出,因为它们属于最小的问题范围。所以,初始化往往都是[0][0]以及第0行和第0列。这道题的0行、0列就是根据前一个status递推得到后一个status的情况。总体而言,它是上面的数字三角形的题的矩阵版。
同时,它也用到了短路或的特殊功效。
6、Unique Paths(所有可能的方案数的计数问题)
A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).
The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).
How many possible unique paths are there?
public class Solution {
public int uniquePaths(int m, int n) {
if(m==0 && n==0){
return 0;
}
if(m==1 || n==1){//注意这里不是0
return 1;
}
/*Initialize status array*/
int[][] status = new int[m][n];
status[0][0] = 1;
for(int temp=1; temp这道题在中文注释部分曾经做错。注意m和n的矩阵的行数和列数,所以特殊的情况是1而不是0.
7、Unique Paths II(有障碍物的情况,加几个if)
Now consider if some obstacles are added to the grids. How many unique paths would there be?
An obstacle and empty space is marked as 1 and 0 respectively in the grid.
public class Solution {
/**
* @param obstacleGrid: A list of lists of integers
* @return: An integer
*/
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
// write your code here
if(obstacleGrid == null || obstacleGrid.length == 0
|| obstacleGrid[0] == null || obstacleGrid[0].length == 0){
return 0;
}
if(obstacleGrid[0][0] == 1){
return 0;
}
int row = obstacleGrid.length;
int col = obstacleGrid[0].length;
int index_col = 1;
int index_row = 1;
int[][] status = new int[row][col];
status[0][0] = 1;
//initialize row 0
for(;index_col这道题犯过的错是如果本来的矩阵在0,0的位置就是一个障碍物,则属于返回0种路径的情况。在返回零的特殊情况一开始并没有考虑到。
然后题目需要注意的点是,只有1行或者1列的特殊情况(不用初始化状态矩阵,但需要考虑存在0)。还有在初始化0行、0列的状态矩阵时需要考虑0。以及一般填充时,遇到0则把该点status置0。
8、Jump game
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Determine if you are able to reach the last index.
For example:
A = [2,3,1,1,4], return true.
A = [3,2,1,0,4], return false.
这道题是序列型动态规划,判断是序列还是集合的一个重要的条件是,这个数组的元素的顺序是否会影响结果。是的话,这便是一个序列,否则,这是一个集合。
同时,这也是一道是否的问题。而做是否的问题时,应该考虑到只要一从否变为是时,便可以停止搜索进行下一步了。以下便是没考虑到这个问题的代码:
public class Solution {
public boolean canJump(int[] nums) {
/*special cases*/
if(nums == null || nums.length == 0){
return false;
}
/*initilize the status array*/
boolean[] status = new boolean[nums.length];
status[0] = true;
/*fill the status array*/
for(int i=1; i-1;j--){
status[i] = (status[j] && nums[j] >= (i-j)) || status[i];
}
}
return status[nums.length-1];
}
} 以上的代码功能能实现,但超时了。
更改后的方法如下:
public class Solution {
public boolean canJump(int[] nums) {
/*special cases*/
if(nums == null || nums.length == 0){
return false;
}
/*initilize the status array*/
boolean[] status = new boolean[nums.length];
status[0] = true;
/*fill the status array*/
for(int i=1; i-1;j--){
if(status[j] && nums[j] >= (i-j)){
status[i] = true;
break;
}
}
}
return status[nums.length-1];
}
} 9、Jump game II
Follow up for "Unique Paths":
Given an array of non-negative integers, you are initially positioned at the first index of the array.
Each element in the array represents your maximum jump length at that position.
Your goal is to reach the last index in the minimum number of jumps.
For example:
Given array A = [2,3,1,1,4]
The minimum number of jumps to reach the last index is 2. (Jump 1 step from index 0 to 1, then 3 steps to the last index.)
Note:
You can assume that you can always reach the last index.
这道题就回到了最大最小的动态规划问题。而且,这通过不能调换数组元素的顺序可见,这是一个序列。
这道题的一个难点是:如何设置状态的问题。状态是:从零点(起点)开始跳到当前点至少需要多少步。所以,特别需要注意的是,如果是status[0]是等于0的,不能初始化为1.
接下来的逻辑就比较简单:
如果这个点能跳到当前点且status[j] + 1与目前的status[i]比,如果比它更小,则更新status[i]。
代码如下:
public class Solution {
public int jump(int[] nums) {
/*status array的意思是,跳到当前位置最少需要多少步。j= i-j时, min(f[j]+1)*/
if(nums == null || nums.length == 0){
return 0;
}
int[] status = new int[nums.length];
status[0] = 0;
for(int i=1; i-1;j--){
if(nums[j] >= i-j){
status[i] = Math.min(status[i],status[j]+1);
}
}
}
return status[nums.length-1];
}
} 但是,这样的方法还是会有超时的问题。所以,这道题最好方法是贪心算法。
10、Longest Increasing Subsequence
Given an unsorted array of integers, find the length of longest increasing subsequence.
For example,
Given [10, 9, 2, 5, 3, 7, 101, 18],
The longest increasing subsequence is [2, 3, 7, 101], therefore the length is 4. Note that there may be more than one LIS combination, it is only necessary for you to return the length.
Your algorithm should run in O(n2) complexity.(动态规划的方法)
Follow up: Could you improve it to O(n log n) time complexity? (就是二分法,比较巧)
这里的关键是,设立的状态的含义应该是:以当前数字结尾的上升序列最长的是什么。然后是直接在状态序列中选择最大的值作为答案。
public class Solution {
public int lengthOfLIS(int[] nums) {
/*这里需要记住,状态的定义是以当前位置的数字结尾的序列的最长序列长度,最后返回这个状态数组的最长长度即可*/
/*two special cases*/
int return_val = 0;
if(nums == null){
return return_val;
}
if(nums.length == 0 || nums.length == 1){
return nums.length;
}
/*Initilize the status array*/
int[] status = new int[nums.length];
status[0] = 1;
/*fill the status array*/
for(int i=1;i-1;j--){
if(nums[i]>nums[j]){
status[i] = status[i] < (status[j] + 1) ? status[j] + 1 : status[i];
}
}
}
/*get the largest value*/
for(int k=0;kreturn_val){
return_val = status[k];
}
}
return return_val;
}
} 11、House Robber
You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night.
Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police.
这道题如果直接思考,则可以发现有很多的可能的组合,而且很复杂。所以,如果一开始从最后的房子开始看起,前面有很多的组合可能。所以,这就是动态规划这种分治思想的好处,从最小的情况开始考虑起,让之后每种选择都可以轻而易举地选择更优的选择。
例如一个序列是:10 2 2 5 1 1这样的house。
一开始只有一家House时,初始化status[0] = 10;有两家House的时候,初始化status[1] = Math.max(nums[0],nums[1]).
然后从第三家house开始,就可以这么考虑,如果我打劫这家和这家前面的间隔一家的钱加起来(10+2)有没有我打劫旁边那家(第二家)累积的(10)多?如果没有,我干脆只打劫旁边那家好了,所以当前的status也就等于旁边家的status。每一家的status都是积累到当前家的最优获益值。那么,就知道该怎么选择了。
public class Solution {
public int rob(int[] nums) {
if(nums == null || nums.length == 0){
return 0;
}
if(nums.length == 1){
return nums[0];
}
/*Initilize the status array*/
int[] status = new int[nums.length];
status[0] = nums[0];
status[1] = Math.max(nums[0],nums[1]);
/*fill the status array*/
for(int i=2;i12、Climb Stairs
You are climbing a stair case. It takes n steps to reach to the top.
Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?
然后题目只给出了这些stairs有n级。
所以status[i] = status[i-1] + status[i-2]。
status代表的是到当前位置有多少个走法。
public class Solution {
public int climbStairs(int n) {
/*special cases*/
if(n==0){
return 0;
}
if(n==1){
return 1;
}
/*establish the status array*/
int[] status = new int[n];
/*initilize the status array*/
status[0] = 1;
status[1] = 2;
/*fill the status array*/
for(int i=2;i这里看似是一个序列型题目,其实是一个向量型的矩阵型的counting题目。与Unique paths类似。
/****************************************************Linked List题目***********************************************************************/
对于链表的题目,很多时候都是考虑对空指针的提防和处理。当你用到.next的调用的时候,注意想想,这是不是空。另外,当你有调用.next修改其数据域时,就是修改了链表了。
13、Remove Duplicates from Sorted List
Given a sorted linked list, delete all duplicates such that each element appear only once.
For example,
Given 1->1->2, return 1->2.
Given 1->1->2->3->3, return 1->2->3.
这题的做法和insertBefore和Remove是类似的,利用prev和cur两个指针。唯一需要注意的,是我在里面的循环中,忘了考虑空指针的问题:
public class Solution {
public ListNode deleteDuplicates(ListNode head) {
ListNode prev = null;
ListNode tmp = head;
while(tmp != null){
prev = tmp;
tmp = tmp.next;
while(tmp != null && prev.val == tmp.val){//注意tmp!=null,需要考虑空指针问题
prev.next = tmp.next;
tmp = tmp.next;
}
}
return head;
}
}14、Delete Node in a Linked List
Write a function to delete a node (except the tail) in a singly linked list, given only access to that node.
Supposed the linked list is 1 -> 2 -> 3 -> 4 and you are given the third node with value 3, the linked list should become 1 -> 2 -> 4 after calling your function.
public class Solution {
public void deleteNode(ListNode node) {
node.val = node.next.val;
node.next = node.next.next;
}
}这道题是伪删除,搞笑的题,看看就好。
15、Remove Duplicates from Sorted List II
Given a sorted linked list, delete all nodes that have duplicate numbers, leaving only distinct numbers from the original list.
For example,
Given 1->2->3->3->4->4->5, return 1->2->5.
Given 1->1->1->2->3, return 2->3.
这道题属于dummy node的应用题 —— 当你不确定链表头的时候:这题表现在链表头可能会被删掉或者merge linked list的时候也是用同样的情况。
同样的是,复制一个dummy,然后,让复制的节点去冲锋的方式完成。
public class Solution {
public ListNode deleteDuplicates(ListNode head) {
ListNode dummy = new ListNode(-1);
int value;
dummy.next = head;
head = dummy;
while(head.next != null && head.next.next != null){
if(head.next.val == head.next.next.val){
value = head.next.val;
while(head.next != null && head.next.val == value){
head.next = head.next.next;
}
}else{
head = head.next;
}
}
return dummy.next;
}
}16、Reverse LinkedList(现在这种题已经成为基本功的一部分)
Reverse a singly linked list.
首先,判断这道题的链表头是确定的,所以不需要使用dummy node。
思路1:
利用prev和cur来实现两两结点之间的反转。while(cur != null)的循环。
public class Solution {
public ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode tmp = null;
while(head != null){
tmp = head.next;
head.next = prev;
prev = head;
head = tmp;
}
return prev;
}
}思路2:遍历一个链表存进stack,一个一个pop出来连起来。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
import java.util.LinkedList;
class StackLinkedList{
private LinkedList storage;
public StackLinkedList(){
storage = new LinkedList();
}
public void push(AnyType item){
storage.addLast(item);
}
public AnyType pop(){
return storage.removeLast();
}
public boolean isEmpty(){
return (storage.size() == 0);
}
}
public class Solution {
public ListNode reverseList(ListNode head) {
ListNode tmp = head;
ListNode dummy = new ListNode(-1);
head = dummy;
StackLinkedList stackins = new StackLinkedList();
while(tmp != null){
stackins.push(tmp.val);
tmp = tmp.next;
}
while(!(stackins.isEmpty())){
head.next = new ListNode(stackins.pop());
head = head.next;
}
return dummy.next;
}
} 这道题犯了一个交叉引用的错误。如果你放进stack的是一个node的话,假设现在的链表是1-->2,那么pop出来是【2,null】,然后head = head.next,head = 【2,null】,head.next = 【1,2】,则链表成为2 --> 1 --> 2 --> 1...
所以,正确的做法是如上所示,根据每一个值新建一个node即可。
注意,List作为Collection的一种实现,其也有Collection的isEmpty()的方法,实质是return (.size() == 0);
思路3:最简单的方法 —— 使用Collections.reverse()实现
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
import java.util.LinkedList;
import java.util.Collections;
public class Solution {
public ListNode reverseList(ListNode head) {
LinkedList linklist = new LinkedList();
ListNode tmp = head;
ListNode dummy = new ListNode(-1);
dummy.next = head;
head = dummy;
while(tmp != null){
linklist.add(tmp.val);
tmp = tmp.next;
}
Collections.reverse(linklist);
while(!(linklist.isEmpty())){
head.next = new ListNode(linklist.removeFirst());
head = head.next;
}
return dummy.next;
}
} 顺带提一句,对于String 的reverse可以使用StringBuilder.reverse()实现。
后两种思路的空间复杂度都是O(n),不推荐。第一种思路比较提倡。
在这里重新温故一下,LinkedList在Java里可以实现链表、队列和栈。
队列的接口方法是:offer(),在队尾添加元素;element()或者peek(),队头元素取出,但不删除;poll()出队,取出并删除。
栈:addLast(),removeLast即可实现。
其中offer() = addLast(),peek()或者element() == getFirst(),而poll则是remove或者removeFirst()。
17、Reverse LinkedList II
Reverse a linked list from position m to n. Do it in-place and in one-pass.
For example:
Given 1->2->3->4->5->NULL, m = 2 and n = 4,
return 1->4->3->2->5->NULL.
Note:
Given m, n satisfy the following condition:
1 ≤ m ≤ n ≤ length of list.
这道题典型的属于链表头不确定的情况,所以应该使用dummy node去实现。
从这题开始,介绍链表题目的思考套路 —— 把解题步骤分为几个基本步骤的组合。
以这题为例,首先,链表反向是需要两个指针去实现的。在我们找到了需要反转的位置后,需要做的事情和上一题差不多。第二,这道题需要做的还有把反转区间的前一个节点改变指向而改变指向反转区间的上一个节点。最后,考虑空指针和极端情况即可。
新链表的反转区间前一个节点的指向很好解决(使用dummy node原理),后面的节点接上去需要人为接驳。
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
public class Solution {
public ListNode reverseBetween(ListNode head, int m, int n) {
if(head == null || m<1 || m==n){
return head;
}
ListNode prev = null;
ListNode dummy = new ListNode(-1);
dummy.next = head;
head = dummy;
/*确定开头*/
for(int i=0;head != null && i画出图的效果是:
写出来的更好明白的代码:
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
public class Solution {
public ListNode reverseBetween(ListNode head, int m, int n) {
if(head == null || m==n){
return head;
}
ListNode dummy = new ListNode(-1);
dummy.next = head;
head = dummy;
int count = m-1;
ListNode frontend = null;
ListNode backend = null;
/*for reverse used*/
ListNode prev = null;
ListNode tmp = null;
//确定frontend和backend的位置
while(head!=null && count>0){
head = head.next;
count--;
}
frontend = head;
backend = head.next;
//开始进入反转区,准备反转
head = head.next;
//反转开始
count = n-m+1;
while(head!=null && count>0){
tmp = head.next;
head.next = prev;
prev = head;
head = tmp;
count--;
}
//链接头尾
backend.next = head;
frontend.next = prev;
return dummy.next;
}
}18、Partition List
Given a linked list and a value x, partition it such that all nodes less than x come before nodes greater than or equal to x.
You should preserve the original relative order of the nodes in each of the two partitions.
For example,
Given 1->4->3->2->5->2 and x = 3,
return 1->2->2->4->3->5.
这道题属于左右两边的开头都不确定的,所以应该使用两个dummy node去构造两边的链表。
public class Solution {
public ListNode partition(ListNode head, int x) {
if(head == null){
return null;
}
ListNode leftdummy = new ListNode(-1);
ListNode rightdummy = new ListNode(-1);
ListNode left = leftdummy;
ListNode right = rightdummy;
while(head != null){
if(head.val < x){
left.next = new ListNode(head.val);
left = left.next;
}else{
right.next = new ListNode(head.val);
right = right.next;
}
head = head.next;
}
left.next = rightdummy.next;
return leftdummy.next;
}
}19、Reorder List
Given a singly linked list L: L0→L1→…→Ln-1→Ln,
reorder it to: L0→Ln→L1→Ln-1→L2→Ln-2→…
You must do this in-place without altering the nodes' values.
For example,
Given {1,2,3,4}, reorder it to {1,4,2,3}.
这道题也是典型的可以把实现分为几个基本步骤的题目。首先,直觉上的做法是:利用头尾两个指针,头指针取一个元素,指向下一个。尾指针取一个元素,指向前一个。如此交替到指向之间元素后,即可得到结果。但是,singly link list是不能向前的,所以要想办法实现尾指针从最后向中间元素的连续取值。
技巧就是:我们首先reverse后半段的list,然后再实现交替取值。
最后,由于最后需要重构链表,所以还是需要dummy node。实现的时候,记得考虑空指针和极端情况即可。
综上所述,这道题 = reverse + find middle。
后期第二次做的时候,重新写了一份思路比较清晰的代码。(注意,当涉及到重组一个新的链表,像这题这样的,组合两个链表,最好还是使用dummy node,做法如这份代码所示):
public class Solution {
public void reorderList(ListNode head) {
if(head==null || head.next==null || head.next.next==null){
return;
}
//search for the mid point
ListNode fast = head.next;
ListNode slow = head;
while(fast!=null && fast.next!=null){
fast = fast.next.next;
slow = slow.next;
}
//break the linkedlist and begin to reverse the latter one
ListNode after_mid = slow.next;
ListNode sec_head = after_mid;
ListNode prev = null;
ListNode tmp = null;
slow.next = null;
//reverse the second linked list
while(sec_head != null){
tmp = sec_head.next;
sec_head.next = prev;
prev= sec_head;
sec_head = tmp;
}
//prev is the new head of new linkedlist
sec_head = prev;
ListNode dummy = new ListNode(-1);
ListNode new_head = dummy;
//re-construct the new linked list
while(head != null && sec_head != null){
new_head.next = head;
head = head.next;
new_head = new_head.next;
new_head.next = sec_head;
sec_head = sec_head.next;
new_head = new_head.next;
}
while(head != null){
new_head.next = head;
head = head.next;
new_head = new_head.next;
}
while(sec_head != null){
new_head.next = sec_head;
sec_head = sec_head.next;
new_head = new_head.next;
}
head = dummy.next;
}
}20、Remove Nth Node From End of List
Given a linked list, remove the nth node from the end of list and return its head.
For example,
Given linked list: 1->2->3->4->5, and n = 2.
After removing the second node from the end, the linked list becomes 1->2->3->5.
首先,永远记住一点,做链表的题目前,先思考结果的链表的表头是否是确定的,很明显这题就是不确定的。所以,用dummy node。昨天一开始上来做,就没想那么多,直接用08722的课上的方法,发现有以下问题:
1)要删除倒数Nth节点,你需要的是它的前一个节点;
2)根据第一点的情况,有两种解决方法:1,使用伪删除;2,让fast再先跑一步;(也就是n == 1的时候,fast也要向前一步)。但是这两个方法都有问题,都是没有办法删除头结点(需要dummy node)。
所以,如果一开始就知道应该用dummy node,这题就很容易了。而且,在写程序的过程中,写到了.next的时候,空指针的问题:
public class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
/*首先,确定链表头是否是确定的,这题不确定,所以要用dummy node*/
ListNode dummy = new ListNode(-1);
dummy.next = head;
head = dummy;
//define fast pointer, slow pointer, tmp pointer
ListNode fast = head;
ListNode slow = head;
ListNode tmp = null;
//move the fast pointer to Nth ahead
for(int t=0; t21、Linked List Cycle I 和 Linked List Cycle II
这两道题都是应该背下来的。I只需要判断该链表有没有环:快慢两个指针,快指针走两步,慢指针走一步,如果重合了,就是有环。如果fast到了链表尾(fast.next == null),或者fast为null,则是无环。
public class Solution {
public boolean hasCycle(ListNode head) {
if(head == null || head.next == null){
return false;
}
ListNode fast = head.next;
ListNode slow = head;
while(fast != slow){
if(fast == null || fast.next == null){
return false;
}
fast = fast.next.next;
slow = slow.next;
}
return true;
}
}而II则是如果有环,需要找到环的头,无环返回null:
public class Solution {
public ListNode detectCycle(ListNode head) {
if(head == null || head.next == null){
return null;
}
ListNode fast = head.next;
ListNode slow = head;
while(fast != slow){
if(fast == null || fast.next == null){
return null;
}
fast = fast.next.next;
slow = slow.next;
}
while(head != slow.next){
head = head.next;
slow = slow.next;
}
return head;
}
}背住while(head != slow.next)就一直走,走到是为止,就是环的开头。
22、Copy List with Random Pointer
A linked list is given such that each node contains an additional random pointer which could point to any node in the list or null.
Return a deep copy of the list.
1) 直接的方法,需要O(n)的空间复杂度(用HashMap)
/*
Use HashMap to solve this problem
*/
public class Solution {
public RandomListNode copyRandomList(RandomListNode head) {
if(head == null){
return null;
}
//travsal the linked list, make a new singly linked list without connection
HashMap storage = new HashMap();
RandomListNode ptr = head;
while(ptr != null){
storage.put(ptr,new RandomListNode(ptr.label));
ptr = ptr.next;
}
//connect the new linked list
ptr = head;
while(ptr != null){
storage.get(ptr).next = storage.get(ptr.next);
storage.get(ptr).random = storage.get(ptr.random);
ptr = ptr.next;
}
return storage.get(head);
}
} 建议采用上述的分步写法,思维清晰可辩。
2)使用比较巧的方法:
这种方法的空间复杂度是O(1),
第一遍先把节点复制,然后新的节点放在旧的节点后面。
此时先不复制random域,等到所有的复制节点都齐了,再扫一次链表,写上random域的同时,拆分链表以获得复制的链表。
代码参考:http://www.jiuzhang.com/solutions/copy-list-with-random-pointer/
自己写出来的代码:
/*
Use tricky way
*/
public class Solution {
public RandomListNode copyRandomList(RandomListNode head) {
if(head == null){
return null;
}
RandomListNode tmp = null;
/*for first travsal*/
RandomListNode cur = head;
RandomListNode prev = null;
RandomListNode copy_head = null;
/*for second travsal*/
RandomListNode dummy_org = null;
while(cur != null){
prev = cur;
cur = cur.next;
tmp = new RandomListNode(prev.label);
prev.next = tmp;
tmp.next = cur;
}
/*settle the random*/
dummy_org = new RandomListNode(-1);
dummy_org.next = head;
head = dummy_org;
while(head != null && head.next != null){
if(head.next.random != null){
head.next.next.random = head.next.random.next;
}
head = head.next.next;
}
head = dummy_org.next;
copy_head = head.next;
/*split the list*/
while(head!=null){
tmp = head.next;
head.next = tmp.next;
head = head.next;
if(tmp.next != null){
tmp.next = tmp.next.next;
}
}
return copy_head;
}
}/******************************************Graph******************************************/
下面讲图论的题目。关于图的基本知识,请见:http://blog.csdn.net/firehotest/article/details/53503624
24、同样是deep copy的题目,不过这次是deep copy一个graph的题目。
Clone Graph
Clone an undirected graph. Each node in the graph contains a label and a list of its neighbors.
OJ's undirected graph serialization:
Nodes are labeled uniquely.
We use # as a separator for each node, and , as a separator for node label and each neighbor of the node.
As an example, consider the serialized graph {0,1,2#1,2#2,2}.
The graph has a total of three nodes, and therefore contains three parts as separated by #.
First node is labeled as 0. Connect node 0 to both nodes 1 and 2.
Second node is labeled as 1. Connect node 1 to node 2.
Third node is labeled as 2. Connect node 2 to node 2 (itself), thus forming a self-cycle.
Visually, the graph looks like the following:
1
/ \
/ \
0 --- 2
/ \
\_/
这道题的思路和copy linked list一样,利用hashset存起新老节点的关系,然后重构新节点的链接。
不过,对于图而言,具体到就是这题的连通图,还需要掌握如何通过一个节点遍历整幅图的节点。有BFS和DFS两种方法:下面先给出BFS的方法。
这道题,主要是复习了图的DFS和BFS。
/**
* Definition for undirected graph.
* class UndirectedGraphNode {
* int label;
* List neighbors;
* UndirectedGraphNode(int x) { label = x; neighbors = new ArrayList(); }
* };
*/
public class Solution {
public UndirectedGraphNode cloneGraph(UndirectedGraphNode node) {
if(node == null){
return node;
}
//get all the nodes
ArrayList node_list = travsal(node);
//establish a hashmap to copy nodes
HashMap orig_copy =
new HashMap();
for(UndirectedGraphNode iter : node_list){
orig_copy.put(iter, new UndirectedGraphNode(iter.label));
}
//establish the connections
for(UndirectedGraphNode iter : node_list){
UndirectedGraphNode tmp = orig_copy.get(iter);
for(UndirectedGraphNode neighbour : iter.neighbors){
tmp.neighbors.add(orig_copy.get(neighbour));
}
}
return orig_copy.get(node);
}
//BFS
private ArrayList travsal(UndirectedGraphNode node){
Queue buf = new LinkedList();
Set return_set = new HashSet();
buf.offer(node);
while(!(buf.isEmpty())){
UndirectedGraphNode tmp = buf.poll();
if(return_set.add(tmp)){
for(UndirectedGraphNode iter : tmp.neighbors){
buf.offer(iter);
}
}
}
return new ArrayList(return_set);
}
} 记住,凡是Map的关系都是两两一对的key value的关系。在初始化的时候,千万别忘了。
下面再来做DFS遍历的方法:
使用递归的DFS
/**
* Definition for undirected graph.
* class UndirectedGraphNode {
* int label;
* List neighbors;
* UndirectedGraphNode(int x) { label = x; neighbors = new ArrayList(); }
* };
*/
public class Solution {
public UndirectedGraphNode cloneGraph(UndirectedGraphNode node) {
if(node == null){
return node;
}
//get all the nodes
Set return_set = new HashSet();
travsal(node, return_set);
ArrayList node_list = new ArrayList(return_set);
//establish a hashmap to copy nodes
HashMap orig_copy =
new HashMap();
for(UndirectedGraphNode iter : node_list){
orig_copy.put(iter, new UndirectedGraphNode(iter.label));
}
//establish the connections
for(UndirectedGraphNode iter : node_list){
UndirectedGraphNode tmp = orig_copy.get(iter);
for(UndirectedGraphNode neighbour : iter.neighbors){
tmp.neighbors.add(orig_copy.get(neighbour));
}
}
return orig_copy.get(node);
}
//DFS, 这里采用遍历的方法
private void travsal(UndirectedGraphNode node, Set return_set){
if(!(return_set.add(node))){
return;
}
for(UndirectedGraphNode tmp : node.neighbors){
travsal(tmp,return_set);
}
return;
}
} 使用非递归的DFS:
/**
* Definition for undirected graph.
* class UndirectedGraphNode {
* int label;
* List neighbors;
* UndirectedGraphNode(int x) { label = x; neighbors = new ArrayList(); }
* };
*/
public class Solution {
public UndirectedGraphNode cloneGraph(UndirectedGraphNode node) {
if(node == null){
return node;
}
//get all the nodes
ArrayList node_list = travsal(node);
//establish a hashmap to copy nodes
HashMap orig_copy =
new HashMap();
for(UndirectedGraphNode iter : node_list){
orig_copy.put(iter, new UndirectedGraphNode(iter.label));
}
//establish the connections
for(UndirectedGraphNode iter : node_list){
UndirectedGraphNode tmp = orig_copy.get(iter);
for(UndirectedGraphNode neighbour : iter.neighbors){
tmp.neighbors.add(orig_copy.get(neighbour));
}
}
return orig_copy.get(node);
}
//DFS non recursive
private ArrayList travsal(UndirectedGraphNode node){
LinkedList stack = new LinkedList();
Set return_set = new HashSet();
stack.addLast(node);
while(!(stack.isEmpty())){
UndirectedGraphNode tmp = stack.removeLast();
if(return_set.add(tmp)){
for(UndirectedGraphNode iter : tmp.neighbors){
stack.addLast(iter);
}
}
}
return new ArrayList(return_set);
}
} 这里需要注意非递归的版本,关键善用set.add函数来判断是否应该继续加进入queue或者stack。