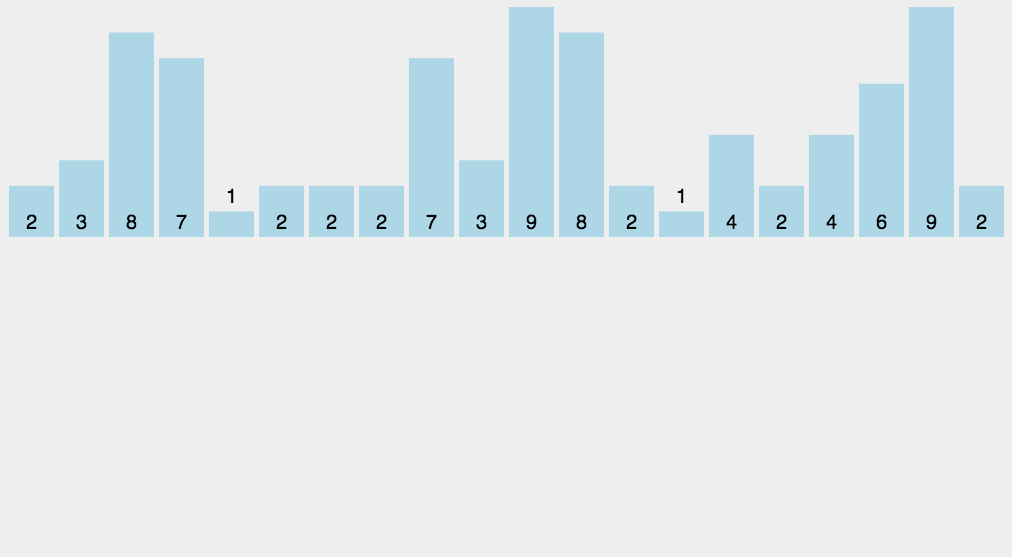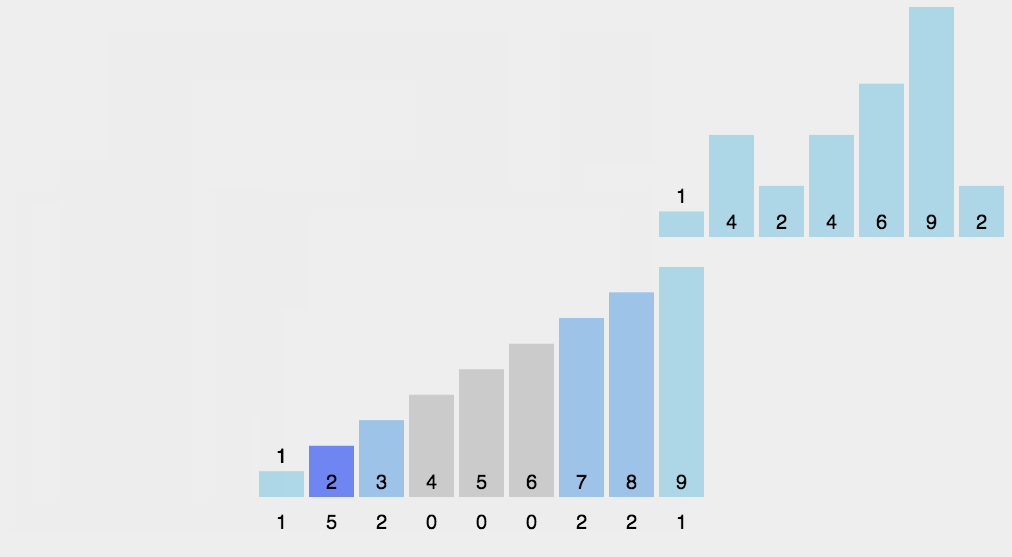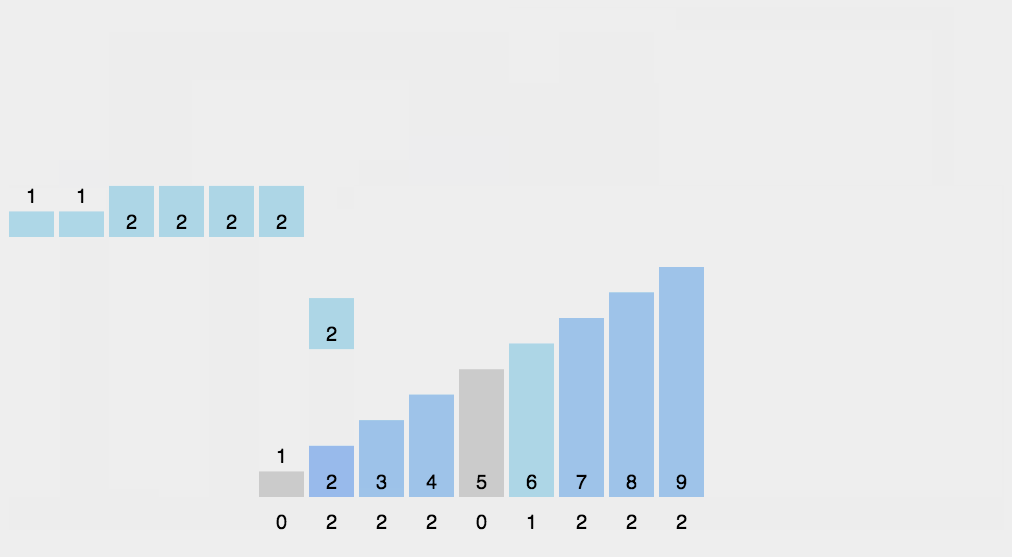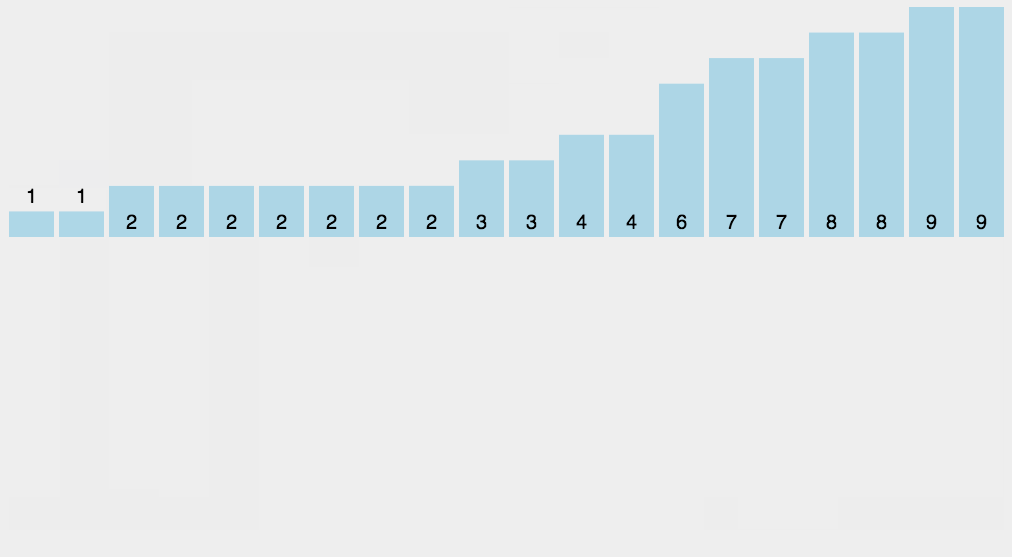十大经典排序算法——计数排序、桶排序、基数排序

计数排序

算法步骤

• 找出待排序的数组中最大和最小的元素
• 统计数组中每个值为i的元素出现的次数，存入数组C的第i项
• 对所有的计数累加（从C中的第一个元素开始，每一项和前一项相加）
• 反向填充目标数组：将每个元素i放在新数组的第C(i)项，每放一个元素就将C(i)减去1

具体步骤

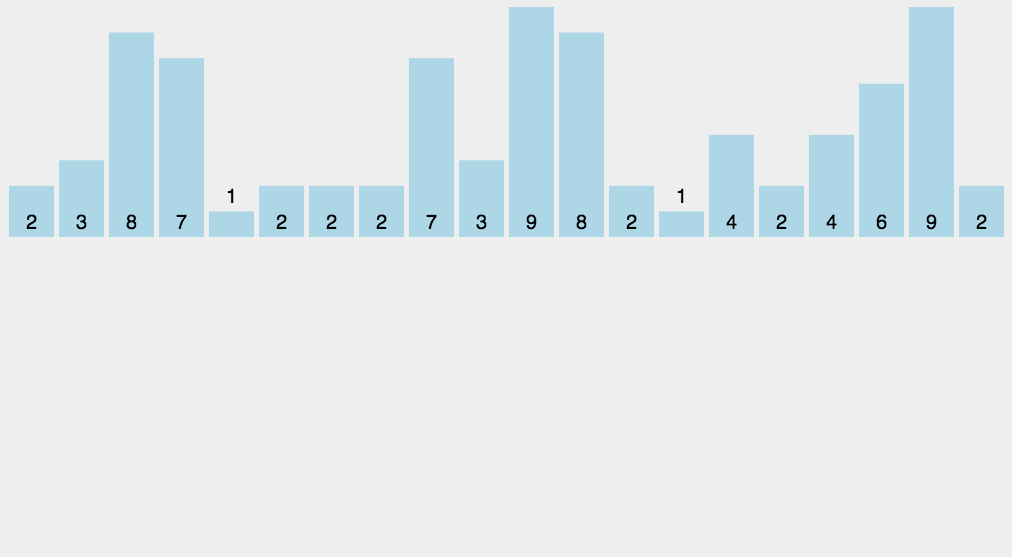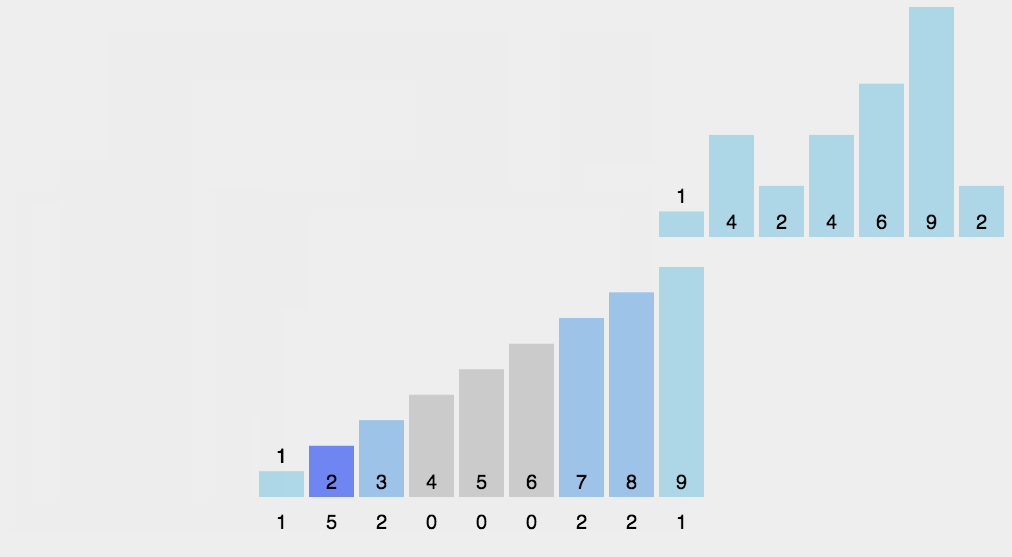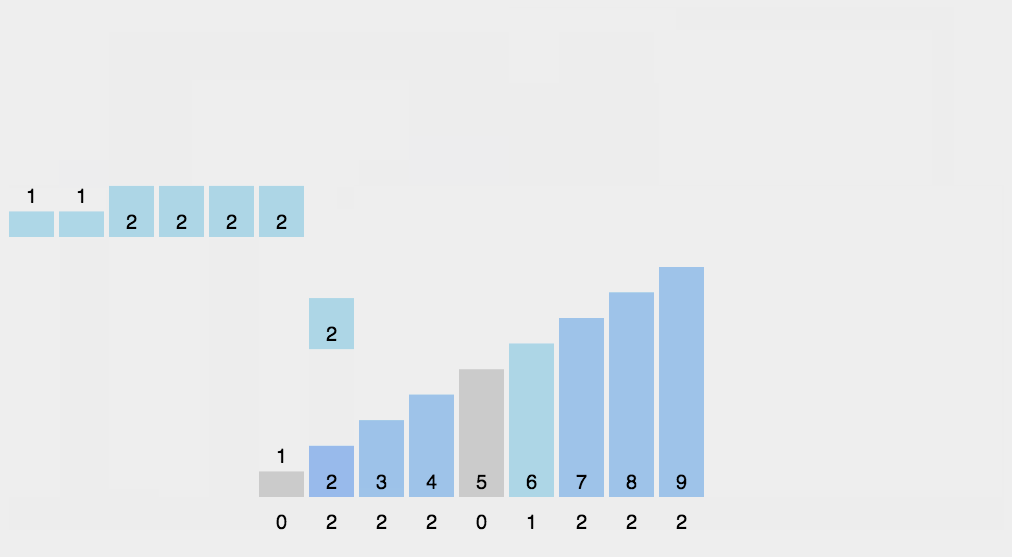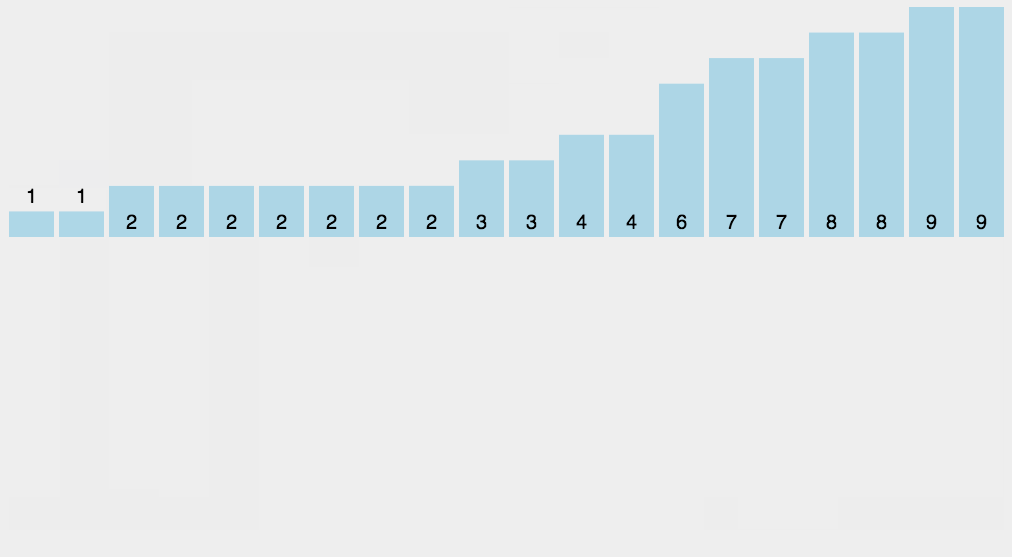
代码实现

def count_sort(arr,maxValue):
    bucketlen = maxValue +1
    bucket = [0]*bucketlen #创建统计数组
    sortedIndex = 0
    arrlen = len(arr)
    for i in range(arrlen):
        if not bucket[arr[i]]:
            bucket[arr[i]] = 0
        bucket[arr[i]] += 1
    for j in range(bucketlen):
        while bucket[j] > 0:
            arr[sortedIndex] = j
            sortedIndex += 1
            bucket[j] -= 1
    return arr
        

测试

arr = [54,26,93,17,77,31,44,55,20]
count_sort(arr,max(arr))
print(arr)

[17, 20, 26, 31, 44, 54, 55, 77, 93]

桶排序

算法步骤

• 建立一堆buckets，每个
• 遍历原始数组，并将数据放入到各自的buckets当中
• 对非空的buckets进行排序
• 按照顺序遍历这些buckets并放回到原始数组中即可构成排序后的数组

具体步骤

代码实现

def bucketSort(arr):
  # 选择一个最大的数
  max_arr = max(arr)
  # 创建一个元素全是0的列表, 当做桶
  bucket = [0]*(max_arr+1)
  # 把所有元素放入桶中, 即把对应元素个数加一
  for i in arr:
    bucket[i] += 1
  # 存储排序好的元素
  sort_arr = []
  # 取出桶中的元素
  for j in range(len(bucket)):
    if bucket[j] != 0:
      for y in range(bucket[j]):
        sort_arr.append(j)
  
  return sort_arr

测试

arr = [54,26,93,17,77,31,44,55,20]
arr = bucketSort(arr)
print(arr)

[17, 20, 26, 31, 44, 54, 55, 77, 93]

基数排序

算法步骤

• 根据个位数的数值，在遍历数组时将它们分配至编号0到9的桶中
• 将这些桶中的数值重新串接起来，根据十位数分配
• 将这些桶中的数值重新串接起来，构成排序好的数列

具体步骤

代码实现

def RadixSort(a):
    i = 0                                             #初始为个位排序
    n = 1                                           #最小的位数置为1（包含0）
    max_num = max(a)                       #得到带排序数组中最大数
    while max_num > 10**n:              #得到最大数是几位数
        n += 1
    while i < n:
        bucket = {}                             #用字典构建桶
        for x in range(10):
            bucket.setdefault(x, [])    #将每个桶置空
        for x in a:                               #对每一位进行排序
            radix =int((x / (10**i)) % 10)   #得到每位的基数
            bucket[radix].append(x) #将对应的数组元素加入到相应位基数的桶中
        j = 0
        for k in range(10):
            if len(bucket[k]) != 0:       #若桶不为空
                for y in bucket[k]:         #将该桶中每个元素
                    a[j] = y                       #放回到数组中
                    j += 1
        i += 1

测试

arr = [54,26,93,17,77,31,44,55,20]
RadixSort(arr)
arr

[17, 20, 26, 31, 44, 54, 55, 77, 93]