《机器学习》阅读心得——六、支持向量机
-
-
- 六支持向量机
- 1 间隔与支持向量
- 2 核函数
- 3 软间隔与正则化
- 4 支持向量回归
- 六支持向量机
-
六、支持向量机
6.1 间隔与支持向量
给定训练样本集 D={(x1,y1),(x2,y2),...,(xm,ym)} ,分类学习的思路是在样本空间中找到一个划分超平面,将不同类别的样本分开。在样本空间中,划分超平面可通过以下方程来描述:
ωTx+b=0(6.1)
其中 ω=(ω1;ω2;...;ωd) 为法向量。样本空间中任一点x到超平面的距离可写为
r=|ωTx+b|||ω||(6.2)
假定超平面可以将样本正确分类,即对于 (xi,yi)∈D ,若 yi=+1 ,则有 ωTx+b>0 ;若有 yi=−1 ,则有 ωTx+b<0 。令
{ωTxi+b≥+1,ωTxi+b≤−1,yi=+1yi=−1(6.3)
如下图所示,距离超平面最近的这些训练样本使得上式的等号成立,它们被称为“支持向量”。两个异类支持向量到超平面的距离之和为
γ=2||ω||(6.4)
它被称为“间隔”。
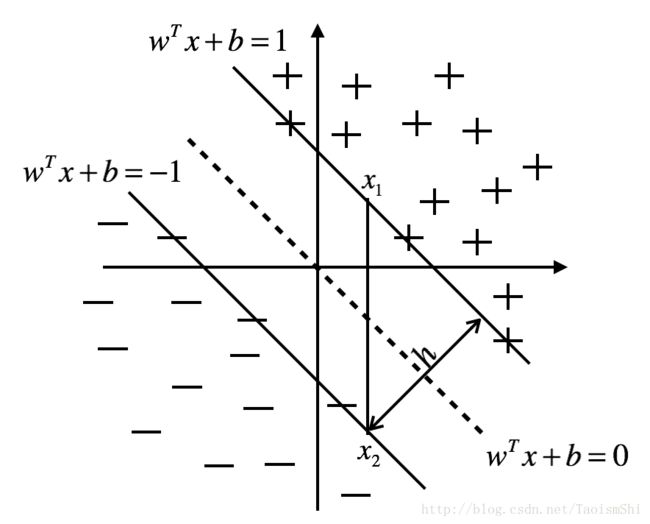
支持向量与间隔
要找到具有最大间隔的超平面,需要找到符合条件的 ω 和 b 使得 γ 最大。经简单转换我们可以得到支持向量机的基本公式
{min12||ω||2s.t.yi(ωTxi+b)≥1(6.5)
当使用拉格朗日乘子法对式(6.5)进行求解后,可以得到式(6.5)的对偶问题如下:
{max∑mi=1αi−12∑mi=1∑mj=1αiαjyiyjxTixjs.t.∑mi=1αiyi=0(6.6)
其中 αi 是拉格朗日乘子。
解出式(6.6)可以得出支持向量机的重要性质: 训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关。
6.2 核函数
当训练样本不是线性可分的,如“异或”问题,可将样本从当前空间映射到一个更高维的特征空间,使得样本在这个空间中线性可分。如果原始空间是有限维,那么一定存在一个合适的高维特征空间使得样本可分。
令 ϕ(x) 表示将x映射后的特征向量,在特征空间中划分超平面的模型可表示为
f(x)=ωTϕ(x)+b(6.7)
类似式(6.5),可以得到
{min12||ω||2s.t.yi(ωTϕ(xi)+b)≥1(6.8)
该式的对偶问题是
{max∑mi=1αi−12∑mi=1∑mj=1αiαjyiyjϕ(xi)Tϕ(xj)s.t.∑mi=1αiyi=0(6.9)
由于高维空间的维度可能很大,直接计算 ϕ(xi)Tϕ(xj) 通常是困难的。为了避开这个问题,可以设想这样一个函数
κ(xi,xj)=ϕ(xi)Tϕ(xj)(6.10)
由此,式(6.9)可以进行简化,进行求解后可以得到
⎧⎩⎨⎪⎪f(x)=ωTϕ(x)+b=∑mi=1αiyiϕ(xi)Tϕ(xj)+b=∑mi=1αiyiκ(xi,yi)+b(6.11)
该式显示模型最优解可以通过训练样本的核函数展开,这个式子也被称为“支持向量展式”。只要一个对称函数所对应的核矩阵半正定,它就能作为核函数使用。核函数的选择对于支持向量机的性能非常重要,如果核函数选择不合适,很可能导致支持向量机性能不佳。
6.3 软间隔与正则化
在现实任务中,往往很难确定合适的核函数使得训练样本在特征空间中线性可分,退一步说,即使找到了核函数使得训练集线性可分,也很难断定这个结果是不是由于过拟合造成的。
缓解该问题的一个方法是允许支持向量机在一些样本上出错,即允许一部分样本不满足约束
yi(ωTxi+b)≥1(6.12)
在最大化间隔的同时,不满足约束的样本应当尽可能少,所以优化目标可以写为
min12||ω2||+C∑i=1mL0/1(yi(ωTxi+b)−1)(6.13)
其中C>0是一个常数, L0/1 是“0/1损失函数”
L0/1(z)={1,0,ifz<0otherwise(6.14)
由于 L0/1(z) 非凸,非连续,使得式(6.14)不容易直接求解,所以通常使用其他一些函数代替 L0/1(z) ,称为“替代损失”。以下是三种替代损失函数
⎧⎩⎨⎪⎪Lhinge(z)Lexp(z)Llog(z)=max(0,1−z)=e−z=log(1+e−z)
当我们采用hinge函数进行求解后可知,此时软间隔向量机的最终模型仅与支持向量有关,即仍保持了稀疏性。一般地,当我们用别的函数替换0/1损失函数时,可以得到一个通用的目标公式
minΩ(f)+C∑i=1mL(f(xi),yi)(6.15)
其中 Ω(f) 称为“结构风险”,用来描述划分超平面的“间隔”大小。第二项称为“经验风险”,描述训练集的误差。
6.4 支持向量回归
给定训练样本 D={(x1,y1),(x2,y2),...(xm,ym)} 。对样本 (x,y) ,支持向量回归(SVR)能够容忍 f(x) 与y之间最多有 ε 的偏差,即仅当 f(x) 与y之间的差别绝对值大于 ε 时才计算损失。这相当于以f(x)为中心,构建一个宽度为 2ε 的隔离带。若样本落入此隔离带内,则被认为是预测正确的。

于是,SVR问题可化为
min12||ω||2+C∑i=1mLε(f(xi)−yi)(6.16)
其中C为正则化常数, Lε 为 ε -不敏感损失函数
Lε(z)={0,|z|−ε,if|z|≤εotherwise(6.17)
引入拉格朗日乘子法可解得SVR的支持向量是落在 ε 隔离带之外的样本,因此它的解具有稀疏性。SVR可表示为
f(x)=∑i=1m(αi^−αi)κ(x−xi)+b(6.18)
其中 κ(xi,xj)=ϕ(xi)Tϕ(xj) 为核函数。