《机器学习》周志华西瓜书习题参考答案：第2章 - 模型评估与选择
【机器学习】《机器学习》周志华西瓜书 笔记/习题答案 总目录
- https://blog.csdn.net/TeFuirnever/article/details/96178919
——————————————————————————————————————————————————————
- 【机器学习】《机器学习》周志华西瓜书读书笔记：第2章 - 模型评估与选择
习题
按照题意，训练集包含700个样本，测试集包含300个样本。并且为了保证训练集和测试集的类别比例一致，使用分层采样，训练集包含正例反例各350个；测试集包含正例反例个150个。
有多少种划分方式是一个排列组合问题，等于从500个正例中挑选出350个的所有可能组合乘上从500个正例中挑选出350个的所有可能组合。
根据简单的数学排列组合性质 ( 500 350 ) × ( 500 350 ) = ( 500 150 ) × ( 500 150 ) \binom{500}{350} \times \binom{500}{350} = \binom{500}{150} \times \binom{500}{150} (350500)×(350500)=(150500)×(150500)，
所以可能取法应该是 n = C 500 350 × C 500 350 n=C_{500}^{350} \times C_{500}^{350} n=C500350×C500350或者 n = C 500 150 × C 500 150 n=C_{500}^{150} \times C_{500}^{150} n=C500150×C500150。
-
10折交叉验证法：通过分层采样获得10个互斥子集，每个子集包含10个样本，正反例各5个。每次取其中9个子集做训练，1个子集做测试。因为在训练集中两个类别数目相当（都为 9 ∗ 5 = 45 9*5=45 9∗5=45 个），所以只能进行随机猜测，错误率为50%。
-
留一法：每次取一个样本做测试，若取出的样本为正例，那么剩下的训练集中有50个反例，49个正例，因此预测结果为反例，反之亦然。故错误率为100%。（题中说了假定学习算法所产生的模型是将新样本预测为训练样本数较多的类别）
先看看F1值的定义，
F 1 = ( 2 ∗ P ∗ R ) / ( P + R ) F1 = (2 * P * R) / (P + R) F1=(2∗P∗R)/(P+R) ，其中 P = T P / ( T P + F P ) P = TP / (TP + FP) P=TP/(TP+FP) 即查准率（Precision），【预测为正例且真实为正例的数量】/【预测为正例的数量】，说白了关心预测为正样本时的准确率； R = T P / ( T P + F N ) R = TP / (TP + FN) R=TP/(TP+FN) 即查全率（又称召回率Recall），【预测为正例且真实为正例的数量】/【真实为正例的数量】。
F1值计算中对查准率和查全率都同等重视。
再看看BEP值
首先目前很多分类算法输出的都是0-1之间的一个概率值，比如逻辑回归、XGBoost等，分类时的做法是预定一个阈值（典型为0.5），若对样本的输出大于此阈值则归为1类（即正例），那么根据样本的输出值从大到小排序（下文简称为“样本的排序”），排在最前面的即可理解为最有可能为正例的样本，而排在最后的是最不可能为正例的样本。从前往后，逐个将样本预测为正例（即把当前样本的输出值定于为阈值，小于阈值的都为反例），每次计算当前的查准率和查全率，即可得到查全率为横坐标查准率为纵坐标上的一个点，在将所有点按顺利连接后即可得到“P-R曲线”，而BEP（即Break-Event Point，平衡点）是在查全率=查准率时的取值。
讨论：
从定义上看，F1值是在阈值固定时，将所有样本分类完成后，综合查全率和查准率得出的值；而BEP值则是寻求一个阈值使得查全率和查准率相同的情况下得到的（此时BEP = 查全率 = 查准率）。
也就是说BEP值和“样本的排序”紧密相关的，而和样本的预测值大小无关，同样的排序，即使将所有预测值同时乘以 0.5 ，其BEP值也是相同的；但是对于F1值，所有样本都将预测为负例（假定阈值为0.5时），此时F1值为0。
回到题目本身，“若学习器A的F1值比学习器B高，则A的BEP值比B高”，那么若能找到两个学习器BEP值相同，而F1值不同，则题目命题就不成立了。那从上面的讨论中已经有了答案了，想象一下学习器A对样本输出值均为学习器B的两倍，两者BEP值是相同的，A的输出在（0,1）之间，而B的输出在（0,0.5）之间，此时B的 F1 值为0，A的 F1 值是在0-1之间。所以原命题不成立。
ps.个人从直觉上BEP值和F1值是没有明确关系的，在讨论过程中拿“输出值乘以0.5”为例，事实上，想象一下，一串固定排序的点(模型的输出概率值)，只在0-1之间同时前进或者后退（每个点前进步长可以不一样，但是排序不变），其BEP值也不会发生变化，而F1值是不断变化的。
-
真正例率是真实正例中预测为正例的比例；
-
假正例率是真实反例中预测为正例的比率；
-
查准率是预测正例中真实正例的比例；
-
查全率是真实正例中预测为正例的比例；
其中，真正例指模型预测为正例并且预测正确的样例，假正例指模型预测为正例并且预测错误的样例。前缀真实表明在数据集中的真实标记，前缀预测表明模型预测出的标记。
特别地，查全率与真正例率是相等的。
问：试证明 A U C = 1 − ℓ r a n k AUC=1-\ell_{rank} AUC=1−ℓrank
南瓜书——https://datawhalechina.github.io/pumpkin-book/#/
错误率是在阈值固定的情况下得出的，ROC曲线是在阈值随着样本预测值变化的情况下得出的。ROC曲线上的每一个点，都对应着一个错误率。
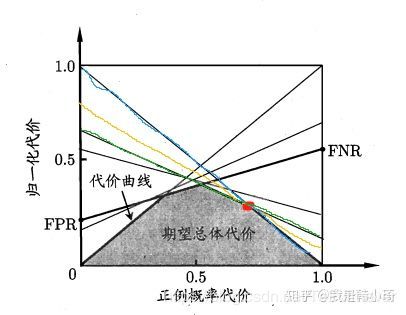
首先“任意一条ROC曲线都有一条代价曲线与之对应”，显然ROC曲线上每个点（FPR，TPR）都对应着下图中一条线段，取所有线段的下届，即可得到唯一的代价曲线。
反之，代价曲线实际上是一个多边形（在有限样本下），易理解，每条边都对应代价平面上一条线段，实际上从左向右遍历每一条边，即可得到ROC曲线上从左到右每一个点。
ps. ROC曲线对应着唯一条代价曲线，但是一条代价曲线可对应着多条不同的ROC曲线，如上图中，在绿、黄、蓝三条线段交于红点时，此时去掉黄色线段代价曲线是不会发生变化的，但是ROC曲线则会少一个点。
M i n − M a x Min-Max Min−Max 规范化
- 优点在于：1、计算相对简单一点。2、当新样本进来时，只有在新样本大于原最大值或者小于原最小值时，才需要重新计算规范化之后的值。
- 缺点在于：1、容易受高杠杆点和离群点影响。
z − s c o r e z-score z−score 规范化
- 优点在于：1、对离群点敏感度相对低一些。
- 缺点在于：1、计算量相对大一些。2、每次新样本进来都需要重新计算规范化。
问：试述卡方检验过程。
根据概率论与数理统计中的内容（交大版本，P239）。卡方检验适用于方差的检验。步骤如下：
1）分均值已知与均值未知两种情况，求得卡方检验统计量；
2）根据备选假设以及α，求得所选假设对应的拒绝域（临界值区间）；
3）根据1）中求得的卡方统计量与2）中求得的拒绝域，判断假设成立与否；
或者可直接参考：卡方检验 - 百度百科
问：试述原始Friedman检验和F检验的区别。
暂时没有思路，以后有机会再补。
参考文章
- 机器学习（周志华）课后习题
- https://blog.csdn.net/snoopy_yuan/article/category/6788615