排序算法吐血整理-附java实现
排序算法吐血整理
标签(空格分隔): java 排序 算法
- 排序算法吐血整理
-
-
- 啰里八嗦
- 插入排序
- 直接插入排序
- 二分法插入排序
- 希尔排序
- 选择排序
- 简单选择排序
- 堆排序
- 交换排序
- 冒泡排序
- 快速排序
- 归并排序
- 基数排序
- 总结
-
-
啰里八嗦
在实习的过程中,学习到了很多课本上没有的东西,框架呀,系统呀等等,很多很多,但是最近智商下线,很多东西有点遗忘,就想要整理一下经典算法方面的东西,算是在闲暇中慢慢找回状态,并试着看看能不能找点灵感,改进一下相关项目的代码。
插入排序
直接插入排序
基本思想:
将一个待排序的数插入到一个已经拍好序的队列中,找一个合适的位置插入。从后向前找到合适的位置,直到全部插入排序为止。
- 选择第一个数作为已排序的数组(子循环),第二个数作为待排序的数,57小于68,跳出子循环:57,68 - 57,68作为已排序的数组,第三个数作为待排序的数,59小于68,覆盖变为57,59,59,继续循环,57小于59跳出子循环,最后将待排序数覆盖为68:57,59,68 - 同理,最后为:52,57,59,68java实现:
public static int[] directSort(int[] arr) {
for (int i = 1; i < arr.length; i++) {
int j;
int temp = arr[i];
//子循环 已排序的数组 找合适的位置进行插入
for (j = i-1; j >= 0; j--) {
if (arr[j] > temp) {
break;
} else {
arr[j+1] = arr[j];
}
}
arr[j+1] = temp;
}
return arr;
}分析算法性能:
数组初始态不同,直接插入排序所耗费的时间有很大差异。如果按序排列好的数组,则每个插入排序的数只需要比较一次即可,时间复杂度O(n),如果是反序的数组,那么每个待排序的数都要比较i-1次,故时间复杂度为O(n^2)
二分法插入排序
基本思想:
在直接插入排序的基础上,为了减少比较次数,快速定位到插入位置,可以使用二分查找。经典图:
分析排序过程:
在插入第i个元素时,对前面的0~i-1元素进行折半,先跟他们
中间的那个元素比,如果小,则对前半再进行折半,否则对后半
进行折半,直到left>right,然后再把第i个元素前1位与目标位置之间
的所有元素后移,再把第i个元素放在目标位置上。java实现
public static int[] binarySort(int[] arr) {
int left, right, middle;
for (int i = 1; i < arr.length; i++) {
left = 0;
right = i - 1;
int j;
int temp = arr[i];
//二分查找到插入的位置
while (right >= left) {
middle = (right + left) / 2;
if (temp < arr[middle]) {
right = middle - 1;
} else {
left = middle + 1;
}
}
for (j = i - 1; j >= left; j--) {
arr[j+1] = arr[j];
}
arr[left] = temp;
}
return arr;
}分析算法性能
二分插入排序的比较次数与待排序记录的初始状态无关,仅依赖于记录的个数。当n较大时,比直接插入排序的最大比较次数少得多。但大于直接插入排序的最小比较次数。算法的移动次数与直接插入排序算法的相同,最坏的情况为n^2/2,最好的情况为n,平均移动次数为O(n^2)。
希尔排序
基本思想:
本质上是分组插入排序,把记录按增量分组,对每组采用直接插入排序,随着增量逐渐减小,所分成的组包含的记录越来越多,当增量的值减小到1时,整个数据合成为一组,构成一组有序记录,则完成排序。经典图:
分析排序过程:
1.设gap增量为n/2=5,那么整个数组将被分为5组,分别是(9,4),(1,8),(2,6),(5,3),(7,5)分别在这5个小组里面进行排序,得到的结果是:4,1,2,3,5,9,8,6,5,7
2.将gap减小,gap=5/2=2,在原有gap的基础上缩减,那么被分为8组(4,2),(1,3),(2,5),(3,9),(5,8),(9,6),(8,5),(6,7),排序后为:2,1,4,3,5,6,5,7,8,9
3.同理最后gap减小2/2=1,排序结果为:1,2,3,4,5,5,6,7,8,9java实现
public static int[] hillSort(int[] arr) {
int gap = arr.length / 2;
while (gap >= 1) {
for (int i = gap; i < arr.length; i++) {
int j;
int temp = arr[i];
for (j = i - gap; j >= 0 && temp < arr[j]; j = j-gap) {
arr[j+gap] = arr[j];
}
arr[j+gap] = temp;
}
gap = gap / 2;
}
return arr;
}算法性能分析
平均时间复杂度:希尔排序的时间复杂度和其增量序列有关系,这涉及到数学上尚未解决的难题;不过在某些序列中复杂度可以为O(n1.3);
选择排序
简单选择排序
基本思想:
每趟从待排序的记录中选出关键字最小的记录,顺序放在已排序的记录序列末尾,直到全部排序结束为止。很简单。经典图:
java实现:
public static int[] selectSort(int[] arr) {
for (int i = 0; i < arr.length - 1; i++) {
int temp = 0;
//记录当前最小值的索引
int index = i;
for (int j = i + 1; j < arr.length; j++) {
if (arr[j] < arr[index]) {
index = j;
}
}
temp = arr[index];
arr[index] = arr[i];
arr[i] = temp;
}
return arr;
}算法性能:
简单选择排序的比较次数与序列的初始排序无关。 假设待排序的序列有 N 个元素,则比较次数总是n(n - 1) / 2。
而移动次数与序列的初始排序有关。当序列正序时,移动次数最少,为 0.
当序列反序时,移动次数最多,为3n(n - 1) / 2。
所以,综合以上,简单排序的时间复杂度为 O(n^2)。
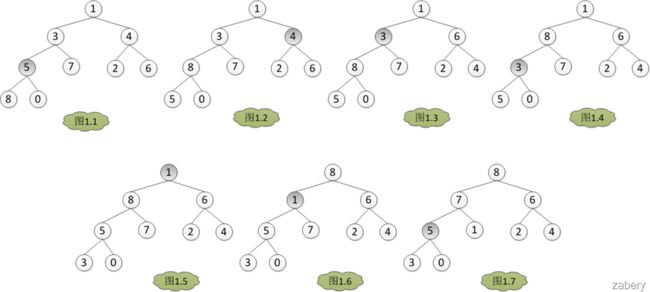
堆排序
基本定义与思想:
二叉堆是完全二叉树或者类似于完全二叉树,分为最大堆和最小堆。
特点:
1.父节点的值总是大于等于(最大堆) 或者小于等于(最小堆)任意自节点的值
2.每个节点的左右子树又是一个二叉堆主要过程就是构建一个最大堆的过程,堆构建的过程从最后一个叶子节点的父节点开始,逐层递减
java实现建堆
//对数组从0到最大索引值建堆
private static void buildMaxHeap(int[] arr, int maxIndex) {
//从最后一个节点的父节点开始
for (int i=(maxIndex-1)/2; i>=0; i--) {
int k = i;//父节点
//如果当前节点的子节点存在
while (k*2+1 <= maxIndex) {
//左子节点
int leftIndex = 2*k+1;
if (leftIndex < maxIndex) {
//如果右子节点比较大
if (arr[leftIndex] < arr[leftIndex+1]) {
//记录右节点的索引值
leftIndex++;
}
}
if (arr[k] < arr[leftIndex]) {
swap(arr, k, leftIndex);
k = leftIndex;
} else {
break;
}
}
}
}算法复杂度
由于最大堆或者最小堆是一颗完全二叉树,那么其算法复杂度应该为建树的复杂度,故为O(log(N))
交换排序
冒泡排序
基本思想:它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
经典图!
java代码实现
public static int[] bubbleSort(int[] arr) {
int length = arr.length;
for (int i=0; ifor (int j=0; j1;j++) {
if (arr[j] < arr[j+1]) {
swap(arr, j, j+1);
}
}
}
return arr;
} 算法性能分析
很简单,2个循环O(n^2)
快速排序
基本思想
选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分
java代码实现
public static int[] quickSort(int[] arr, int low, int high) {
if (low < high) {
//选第一个数作为基准
int pivot = arr[low];
int left = low;
int right = high;
while (left < right) {
while (left < right && arr[right] > pivot) {
right--;
}
arr[left] = arr[right];
while (left < right && arr[left] < pivot) {
left++;
}
arr[right] = arr[left];
}
arr[left] = pivot;
quickSort(arr, low, left-1);
quickSort(arr, right+1, high);
}
return arr;
}
算法性能分析
快速排序是不稳定的排序。
快速排序的时间复杂度为O(nlogn)。
当n较大时使用快排比较好,当序列基本有序时用快排反而不好。
归并排序
基本思想:分而治之,合并为一,将多个有序子数组合并为一个新的有序的数组。
经典图:
java代码实现
public static int[] mergeSort(int[] arr, int left, int right) {
int[] tempArr = new int[arr.length];
if (left < right) {
int middle = (left + right) / 2;
//对左边进行递归
mergeSort(arr, left, middle);
//左边进行递归
mergeSort(arr, middle+1, right);
tempArr = merge(arr, left, middle, right);
}
return tempArr;
}
private static int[] merge(int[] arr, int left, int middle, int right) {
int[] tempArr = new int[arr.length];
int mid = middle+1;
int newIndex = left;
while (left <= middle && mid <= right) {
//从2个数组中选取较小的放入新数组中
if (arr[left] <= arr[mid]) {
tempArr[newIndex++] = arr[left++];
} else {
tempArr[newIndex++] = arr[mid++];
}
}
//不等长将剩余的放入新数组中
while(left <= middle) {
tempArr[newIndex++] = arr[left++];
}
while (mid <= right) {
tempArr[newIndex++] = arr[mid++];
}
return tempArr;
}算法性能分析
归并排序是稳定的排序方法,时间复杂度为O(nlogn)。速度仅次于快速排序,一般用于对总体无序,但是各子项相对有序的数列。
基数排序
基本思想:按照各个分位分别进行排序,将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
经典图:
java代码实现
public static int[] cardinalSort(int[] arr) {
//找到最大数 确定要排序几趟
int max = arr[0];
for (int i=0; i < arr.length; i++) {
if (max < arr[i]) {
max = arr[i];
}
}
//判断有几位
int times = 0;
while (max > 0) {
max/=10;
times++;
}
//建立十个桶
List bukets = new ArrayList();
for (int i=0; i<10; i++) {
ArrayList buket = new ArrayList();
bukets.add(buket);
}
//将相应的数放在相应的桶中
for (int i=0; ifor(int j=0; jint x = arr[j]%(int)Math.pow(10, i+1)/(int)Math.pow(10, i);
ArrayList temp = bukets.get(x);
temp.add(arr[j]);
bukets.set(x,temp);
}
//收集
int count = 0;
for (int k=0; k<10; k++) {
while(bukets.get(k).size()>0) {
ArrayList result = bukets.get(k);
arr[count] = result.get(0);
result.remove(0);
count++;
}
}
}
return arr;
} 算法复杂度
感觉这个算法还是比较有想法的,很神奇。基数排序的时间复杂度为O (nlog(r)m),r为位数,m为基数。
总结
排序算法这个东西总是搞混,一直想把他们理清楚,借这个机会顺便提升一下脑活力。