机器学习笔记——SVM（1）

支持向量机

1、较少数据条件下使用SVM

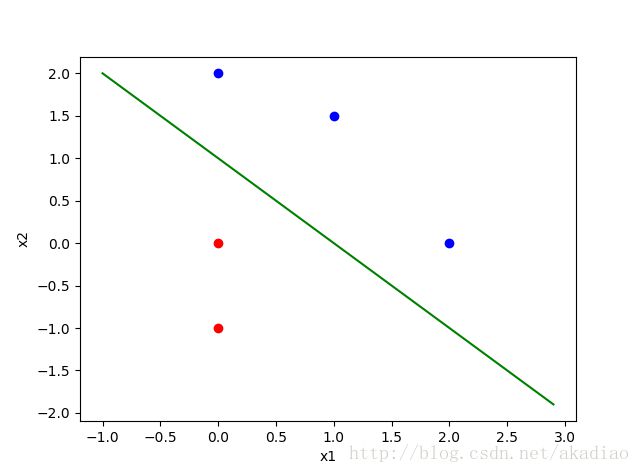
给定空间内5个点，且[0,-1],[0,0]属于R类，[1,1.5],[0,2],[2,0]属于B类：
在空间内分布情况为：

简单计算即可找到两类的分界线：

利用Pychon实现SVM——

代码：

from sklearn import svm

x = [[0,-1],[0,0],[1,1.5],[0,2],[2,0]]
y = [0,0,1,1,1]
clf = svm.SVC(kernel='linear')
clf.fit(x,y)

print clf
print clf.support_vectors_
print clf.support_
print clf.n_support_

y0 = clf.predict([[0,-0.5]])
print y0

首先导入sklearn库的svm模块：

from sklearn import svm

将5个点坐标以list形式存入x内，y内对应每个点的标记<[0,-1],[0,0]标记为0，[1,1.5],[0,2],[2,0]标记为1>;输入sample要按规范输入x = [ [sample1 features] , [sample2 features] … [samplen features] ]：

x = [[0,-1],[0,0],[1,1.5],[0,2],[2,0]]
y = [0,0,1,1,1]

clf = svm.SVC(kernel='linear')
clf.fit(x,y)

打印出结果：

print clf

结果：

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
  decision_function_shape=None, degree=3, gamma='auto', kernel='linear',
  max_iter=-1, probability=False, random_state=None, shrinking=True,
  tol=0.001, verbose=False)

打印出支持向量support_vectors_

print clf.support_vectors_

结果为：

[[ 0. 0.] [ 0. 2.] [ 2. 0.]]

打印出支持向量的索引<即点[ 0. 0.]、 [ 0. 2.]、 [ 2. 0.]在x中的索引>:

print clf.support_

结果为：

[1 3 4]

打印支持向量的个数：

print clf.n_support_

结果为<第一组类中1个，第二类中2个>：

[1 2]

预测新样本的分类，如点[0,-0.5]:

y0 = clf.predict([[0,-0.5]])
print y0

结果为：

[0]

即分为R类中。

2、较大量数据条件下使用SVM

import numpy as np
import pylab as pl
from sklearn import svm

np.random.seed(0)
###返回一个m*n的随机项矩阵
X = np.r_[np.random.rand(20,2)-[2,2],np.random.randn(20,2)+[2,2]]
###生成Y=[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]
Y = [0]*20+[1]*20
##建立SVM模型
clf = svm.SVC(kernel='linear')
clf.fit(X,Y)

###分界线方程为 w0*x+w1*y+b0=0 转换为点斜式为：y=-(w0/w1)*x-(b0/w1) coefficient--系数 intercept--截距
w = clf.coef_[0]
a = -w[0]/w[1]
xx = np.linspace(-5,5)
yy = a*xx-(clf.intercept_[0]/w[1])

###绘制上下边界
###取支持向量中的第1个点，计算与分界线的距离
b = clf.support_vectors_[0]
yy_domn = a*xx+(b[1]-a*b[0])
###取支持向量中的最后1个点，计算与分界线的距离
b = clf.support_vectors_[-1]
yy_up = a*xx + (b[1]-a*b[0])

print "w:",w
print "a:",a
print "support_vectors_\n",clf.support_vectors_
print "clf.coef_:\n",clf.coef_

pl.plot(xx,yy,'k-')
pl.plot(xx,yy_domn,'k--')
pl.plot(xx,yy_up,'k--')

##将边界线上的支撑向量用红色圆圈标记出来
pl.scatter(clf.support_vectors_[:,0],clf.support_vectors_[:,1],s=80,facecolors='none')
pl.scatter(X[:,0],X[:,1], c=Y,cmap=pl.cm.Paired)
pl.axis('tight')
pl.show()

输出为：

w: [ 0.70640203 0.40393883]

a: -1.74878464882 support_vectors_ [[-1.02138166 -1.20084144] [ 1.11221425 0.01920353]] clf.coef_: [[ 0.70640203 0.40393883]]

显示：