人工智能学习笔记-TensorFlow(一)

1安装 TensorFlow

1.1 实验环境

• python2.7
• Tensorflow
• ubuntu 14.04

1.2 安装命令

sudo apt-get update
sudo apt-get install python-pip python-dev
#最近开大会，google的网站链接不上去，下面命令会执行失败
pip install --upgrade https://storage.googleapis.com/tensorflow/linux/cpu/tensorflow-0.8.0-cp27-none-linux_x86_64.whl

#或者去github上下一份代码来自己编译，这个比较痛苦，编译需要java8，cmake大于4.6
https://github.com/tensorflow/tensorflow

2 基本使用简述

2.1 基本概念

• 使用图 (graph) 来表示计算任务
• 在被称之为 会话 (Session) 的上下文 (context) 中执行图
• 使用 tensor 表示数据
• 通过 变量 (Variable) 维护状态
• 使用 feed 和 fetch 可以为任意的操作(arbitrary operation) 赋值或者从其中获取数据

2.2 简单计算演示

通过3+4这样一个最简单的常量加法运算，来演示tensorflow的计算流程

#这段代码描述述了怎么在tensorflow里怎么计算 3+4 这样一个常量计算

import tensorflow as tf
#定义一个常量a为3
a = tf.constant(3.0)
#定义一个常量b为4
b = tf.constant(4.0)
#定义一个op为常量3+4
c = tf.add(a,b)
#以上的代码，我们定义了一个常量相加的图

#启动一个默认的会话
sess = tf.Session()
#用会话来执行我们定义的图
result = sess.run([c])
print result
sess.close()

2.3 传值计算演示

通过定义a+b这样一张图，其中a与b分别是可以被替换的占位符，在会话运算图的时候传入值替换占位符

#这段代码描述了怎么在tensorflow里通过传值来计算 3+4的问题
#首先分别定义可以被替换的op，a与b
#然后定义运算a+b
#在图运算op的时候传值进去

import tensorflow as tf

a = tf.placeholder(tf.float32)
b = tf.placeholder(tf.float32)
c = tf.add(a,b)

result = sess.run([c],feed_dict={a:[3.],b[4.]})
print result
sess.close()

2.4 变量参与计算演示

通过经过一个变量来计算3+4+5这样一个运算，首先把3+4计算的值赋给一个变量，然后再将变量与5相加

什么是变量？
就是在运行的过程中值可以被动态的改变，变量维护图执行过程中的状态信息

#这段代码演示怎么使用变量

import tensorflow as tf
#定义三个相加用的常量：a,b,c
a = tf.constant(3.0)
b = tf.constant(4.0)
c = tf.constant(5.0)
#定义变量v
v = tf.Variable(0.0)
#首先把3与4相加
t = tf.add(a,b)
#把计算得到的t值赋给变量v
update = tf.assign(v,t)
#把变量v的值与5相加
result = tf.add(v,c)
#初始化所有变量的一个操作
init_op = tf.initialize_all_variables()

#启动一个默认的会话
sess = tf.Session()
#执行初始化变量
sess.run(init_op)
#计算3+4并赋值给变量
sess.run(update)
#变量与5相加
result = sess.run(result)
print result
sess.close()

代码中 assign() 操作是图所描绘的表达式的一部分，正如 add() 操作一样。所以在调用 run() 执行表达式之前，它并不会真正执行赋值操作代码中 assign() 操作是图所描绘的表达式的一部分，正如 add() 操作一样。所以在调用 run() 执行表达式之前，它并不会真正执行赋值操作

2.5 神经网络演示

1. 定义添加神经层的函数

   (1) 训练的数据
   (2) 定义节点准备接收数据
   (3) 定义神经层：隐藏层和预测层
   (4) 定义 loss 表达式
   (5) 选择 optimizer 使 loss 达到最小

2. 然后对所有变量进行初始化，通过 sess.run optimizer，迭代 1000 次进行学习

代码如下所示：

#coding=utf-8

import tensorflow as tf
import numpy as np
from matplotlib import pyplot as plt

#定义神经层
#inputs 输入数据
#in_size 输入数据的维度
#out_size 输出数据的维度
#activation_function 激励函数
def add_layer(inputs, in_size, out_size, activation_function=None):
    #定义权重a
    weights = tf.Variable(tf.random_normal([in_size, out_size]))
    #定义偏差b
    biases = tf.Variable(tf.zeros([1,out_size])+0.1)
    #定义公式:y=ax+b
    wx_plus_b = tf.matmul(inputs, weights) + biases
    #dropout率等于0.5的时候效果最好，原因是0.5的时候dropout随机生成的网络结构最多
    #wx_plus_b = tf.nn.dropout(wx_plus_b, keep_prob=0.5)

    if activation_function is None:
        outputs = wx_plus_b
    else:
        outputs = activation_function(wx_plus_b)
    return outputs


#随机生成一份训练数据
x_data = np.linspace(-1,1,300)[:,np.newaxis]
noise = np.random.normal(0,0.05,x_data.shape)
y_data = np.square(x_data) - 0.5 + noise


#定义接受数据的节点
xs = tf.placeholder(tf.float32,[None,1])
ys = tf.placeholder(tf.float32,[None,1])

#添加隐藏层，在隐藏层有10个神经元，使用Relu激活函数
#输入1维数据，经过隐藏层输出10维数据
l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)

#添加输出层，输入是隐藏层的l1，在预测层输出1个结果
#从隐藏层输入得到的10维数据，经输出层处理输出1维数据
prediction = add_layer(l1, 10, 1, activation_function=None)

#定义loss（损失函数）表达式，预测计算结果与真实结果的误差
loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys-prediction),reduction_indices=[1]))

# 选择使得损失最小的方法，这里选择梯度下降，学习率是0.1
optimizer = tf.train.GradientDescentOptimizer(0.1)
train_step = optimizer.minimize(loss)

#对创建的变量初始化
init = tf.initialize_all_variables()

#启动图
sess = tf.Session()
#从这里开始，tensorflow才真正开始运算

#执行初始化变量操作
sess.run(init)

#迭代训练1000次
for i in range(1000):
    sess.run(train_step, feed_dict={xs:x_data, ys:y_data})
    if i % 50 == 0:
        print(sess.run(loss, feed_dict={xs:x_data, ys:y_data}))

#生成一份验证的数据，在我们训练完的模型上验证下
#在把验证的结果画出线来
plt.scatter(x_data, y_data)
testx = np.linspace(-1,1,1000)[:,np.newaxis]
#print(testx)
testy = sess.run(prediction, feed_dict={xs:testx})
testy = testy.reshape((1000,))
testx = testx.reshape((1000,))
#print(testy)
plt.plot(testx,testy, c='r')
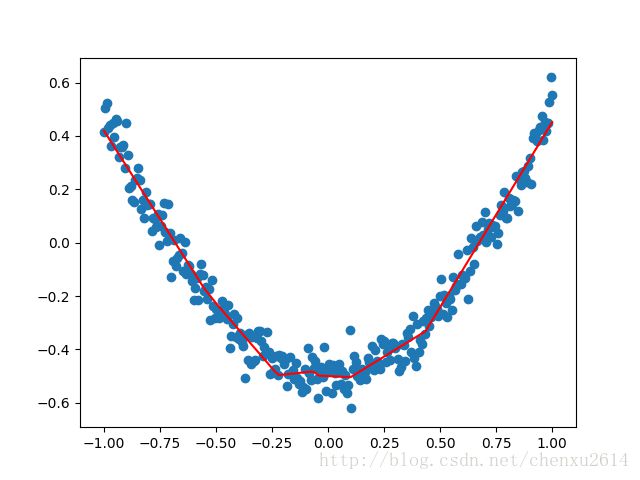
plt.show()

蓝色的点表示训练集上的点，红色线是验证结果，最终结果基本一致

2.6 可视化演示

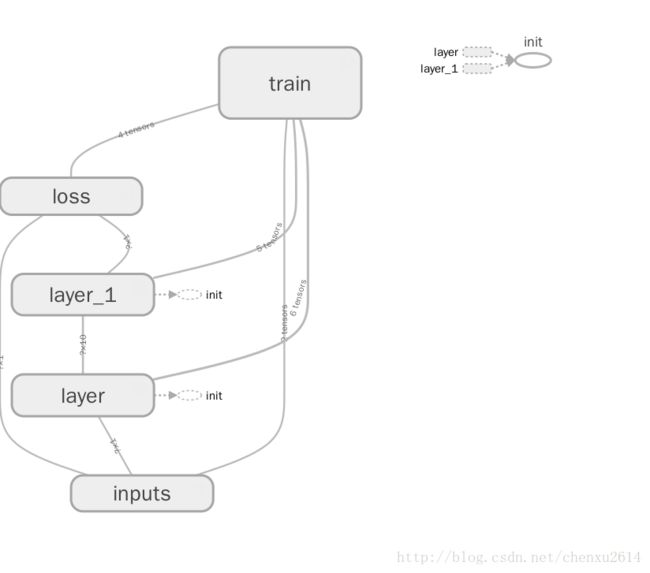
Tensorflow 自带 tensorboard ，可以自动显示我们所建造的神经网络流程图：
就是用 with tf.name_scope 定义各个框架，注意看代码注释中的区别,代码是在上一节代码的基础上修改的：

#coding=utf-8

import tensorflow as tf
import numpy as np
from matplotlib import pyplot as plt

#定义神经层
#inputs 输入数据
#in_size 输入数据的维度
#out_size 输出数据的维度
#activation_function 激励函数
def add_layer(inputs, in_size, out_size, activation_function=None):
    with tf.name_scope('layer'):
        #定义权重a
        with tf.name_scope('weights'):
            weights = tf.Variable(tf.random_normal([in_size, out_size]),name='W')
        #定义偏差b
        with tf.name_scope('biases'):
            biases = tf.Variable(tf.zeros([1,out_size])+0.1, name='b')
        #定义公式:y=ax+b
        with tf.name_scope('wx_plus_b'):
            wx_plus_b = tf.add(tf.matmul(inputs, weights), biases)
        #dropout率等于0.5的时候效果最好，原因是0.5的时候dropout随机生成的网络结构最多
        #wx_plus_b = tf.nn.dropout(wx_plus_b, keep_prob=0.5)

        if activation_function is None:
            outputs = wx_plus_b
        else:
            outputs = activation_function(wx_plus_b)
        return outputs


#随机生成一份训练数据
x_data = np.linspace(-1,1,300)[:,np.newaxis]
noise = np.random.normal(0,0.05,x_data.shape)
y_data = np.square(x_data) - 0.5 + noise


#定义接受数据的节点
with tf.name_scope('inputs'):
    xs = tf.placeholder(tf.float32,[None,1])
    ys = tf.placeholder(tf.float32,[None,1])

#添加隐藏层，在隐藏层有10个神经元，使用Relu激活函数
#输入1维数据，经过隐藏层输出10维数据
l1 = add_layer(xs, 1, 10, activation_function=tf.nn.relu)

#添加输出层，输入是隐藏层的l1，在预测层输出1个结果
#从隐藏层输入得到的10维数据，经输出层处理输出1维数据
prediction = add_layer(l1, 10, 1, activation_function=None)

#定义loss（损失函数）表达式，预测计算结果与真实结果的误差
with tf.name_scope('loss'):
    loss = tf.reduce_mean(tf.reduce_sum(tf.square(ys-prediction),reduction_indices=[1]))

# 选择使得损失最小的方法，这里选择梯度下降，学习率是0.1
with tf.name_scope('train'):
    train_step = tf.train.GradientDescentOptimizer(0.1).minimize(loss)

#对创建的变量初始化
init = tf.initialize_all_variables()

#启动图
sess = tf.Session()
#从这里开始，tensorflow才真正开始运算

writer = tf.summary.FileWriter("logs/", sess.graph)

#执行初始化变量操作
sess.run(init)

#迭代训练1000次
#for i in range(1000):
# sess.run(train_step, feed_dict={xs:x_data, ys:y_data})
# if i % 50 == 0:
# print(sess.run(loss, feed_dict={xs:x_data, ys:y_data}))

#
#plt.scatter(x_data, y_data)
#testx = np.linspace(-1,1,1000)[:,np.newaxis]
#print(testx)
#testy = sess.run(prediction, feed_dict={xs:testx})
#testy = testy.reshape((1000,))
#testx = testx.reshape((1000,))
#print(testy)
#plt.plot(testx,testy, c='r')
#plt.show()

运行完上面代码后,运行命令 tensorboard –logdir=’logs/’ 后会返回一个地址，然后用浏览器打开这个地址，点击 graph 标签栏下就可以看到流程图了：

2.7 保存和加载

训练好了一个神经网络后，可以保存起来下次使用时再次加载，但是TensorFlow 现在只能保存 variables，还不能保存整个神经网络的框架，所以再使用的时候，需要重新定义框架，然后把 variables 放进去学习

# -*- coding: UTF-8 -*- 
import tensorflow as tf
import numpy as np

## Save to file
# remember to define the same dtype and shape when restore
W = tf.Variable([[1,2,3],[3,4,5]], dtype=tf.float32, name='weights')
b = tf.Variable([[1,2,3]], dtype=tf.float32, name='biases')

init= tf.initialize_all_variables()

saver = tf.train.Saver()

# 用 saver 将所有的 variable 保存到定义的路径
with tf.Session() as sess:
  sess.run(init)
  save_path = saver.save(sess, "my_net/save_net.ckpt")
  print("Save to path: ", save_path)

# -*- coding: UTF-8 -*- 
import tensorflow as tf
import numpy as np

# restore variables
# redefine the same shape and same type for your variables
W = tf.Variable(np.arange(6).reshape((2, 3)), dtype=tf.float32, name="weights")
b = tf.Variable(np.arange(3).reshape((1, 3)), dtype=tf.float32, name="biases")

# not need init step

saver = tf.train.Saver()
# 用 saver 从路径中将 save_net.ckpt 保存的 W 和 b restore 进来
with tf.Session() as sess:
    saver.restore(sess, "my_net/save_net.ckpt")
    print("weights:", sess.run(W))
    print("biases:", sess.run(b))

3 激活函数

3.1 什么是激活函数

激活函数（Activation functions）对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。其主要目的是将A-NN模型中一个节点的输入信号转换成一个输出信号。该输出信号现在被用作堆叠中下一个层的输入。激活函数（Activation functions）对于人工神经网络模型去学习、理解非常复杂和非线性的函数来说具有十分重要的作用。它们将非线性特性引入到我们的网络中。其主要目的 是将A-NN模型中一个节点的输入信号转换成一个输出信号。该输出信号现在被用作堆叠中下一个层的输入。
而在A-NN中的具体操作是这样的，我们做输入（X）和它们对应的权重（W）的乘积之和，并将激活函数f（x）应用于其获取该层的输出并将其作为输入馈送到下一个层。而在A-NN中的具体操作是这样的，我们做输入（X）和它们对应的权重（W）的乘积之和，并将激活函数f（x）应用于其获取该层的输出并将其作为输入馈送到下一个层。

3.2 为什么需要激活函数

如果我们不运用激活函数的话，则输出信号将仅仅是一个简单的线性函数。线性函数一个一级多项式。现如今，线性方程是很容易解决的，但是它们的复杂性有限，并且从数据中学习复杂函数映射的能力更小。一个没有激活函数的神经网络将只不过是一个线性回归模型（Linear regression Model）罢了，它功率有限，并且大多数情况下执行得并不好。我们希望我们的神经网络不仅仅可以学习和计算线性函数，而且还要比这复杂得多。同样是因为没有激活函数，我们的神经网络将无法学习和模拟其他复杂类型的数据，例如图像、视频、音频、语音等。这就是为什么我们要使用人工神经网络技术，诸如深度学习（Deep learning），来理解一些复杂的事情，一些相互之间具有很多隐藏层的非线性问题，而这也可以帮助我们了解复杂的数据。

3.3 简介激活的函数的作用

激活函数是用来加入非线性因素的，因为线性模型的表达能力不够。

以下，同种颜色为同类数据。
某些数据是线性可分的，意思是，可以用一条直线将数据分开。比如下图：

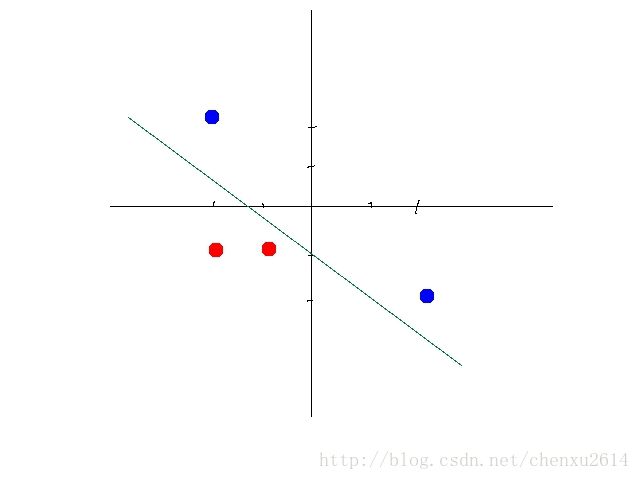
但是有些数据不是线性可分的。比如如下数据：

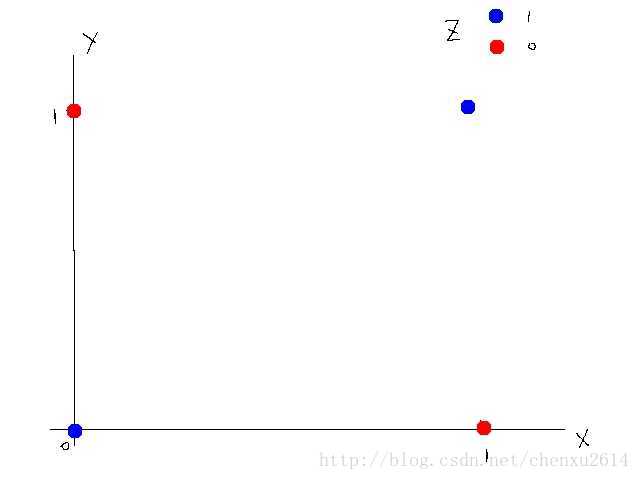
我们可以设计一种神经网络，通过激活函数来使得这组数据线性可分。
激活函数我们选择阀值函数（threshold function），也就是大于某个值输出1（被激活了），小于等于则输出0（没有激活）。这个函数是非线性函数。

神经网络示意图如下：

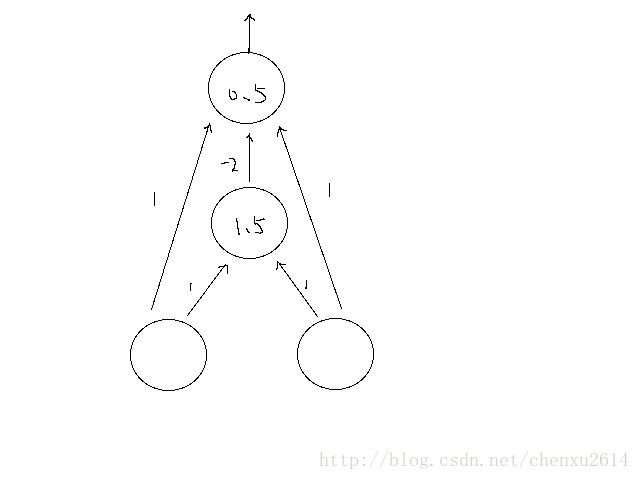
其中直线上的数字为权重。圆圈中的数字为阀值。第二层，如果输入大于1.5则输出1，否则0；第三层，如果输入大于0.5，则输出1，否则0.

我们来一步步算。
第一层到第二层（阀值1.5）

第二层到第三层(阀值0.5)第二层到第三层(阀值0.5)

可以看到第三层输出就是我们所要的xor的答案。
经过变换后的数据是线性可分的（n维，比如本例中可以用平面），如图所示：

总而言之，激活函数可以引入非线性因素，解决线性模型所不能解决的问题。

关于激活函数的内容来自知乎，更多内容参考：知乎-神经网络激励函数

参考文档

• TensorFlow 英文官方网站
• TensorFlow 官方GitHub仓库
• 神经网络之激活函数
• 知乎-神经网络激励函数
• TensorFlow PlayGround