机器学习之Scipy库
1.1 总体说明
SciPy是一款方便、易于使用、专为科学和工程设计的Python工具包。它包括统计、优化、涉及线性代数模块、傅里叶变换、信号和图像处理、常微分方程求解器等众多数学包。
1.2 代表性函数使用介绍
1.最优化
(1)数据建模和拟合
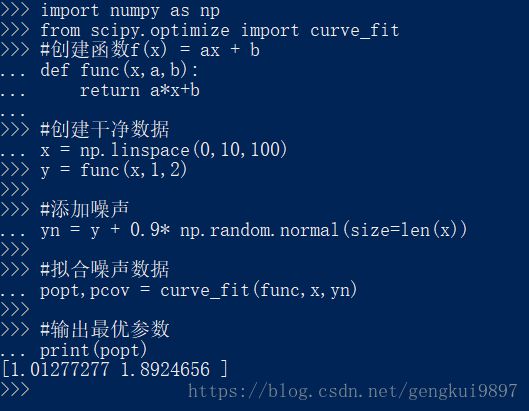
SciPy函数curve_fit使用基于卡方的方法进行线性回归分析。下面,首先使用f(x)=ax+b生成带有噪声的数据,然后使用curve_fit来拟合。
例如:线性回归
import numpy as np
from scipy.optimize import curve_fit
#创建函数f(x) = ax + b
def func(x,a,b):
return a*x+b
#创建干净数据
x = np.linspace(0,10,100)
y = func(x,1,2)
#添加噪声
yn = y + 0.9* np.random.normal(size=len(x))
#拟合噪声数据
popt,pcov = curve_fit(func,x,yn)
#输出最优参数
print(popt)
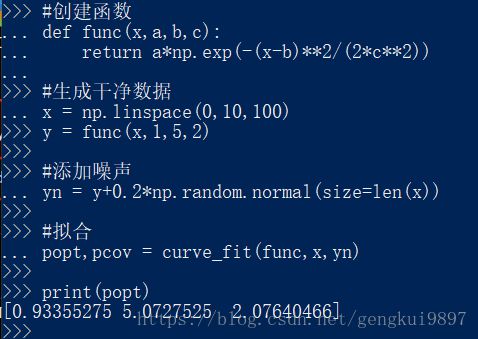
例如:高斯分布拟合
#创建函数
def func(x,a,b,c):
return a*np.exp(-(x-b)**2/(2*c**2))
#生成干净数据
x = np.linspace(0,10,100)
y = func(x,1,5,2)
#添加噪声
yn = y+0.2*np.random.normal(size=len(x))
#拟合
popt,pcov = curve_fit(func,x,yn)
print(popt)
(2)函数求解
SciPy的optimize模块中有大量的函数求解工具,fsolve是其中最常用的
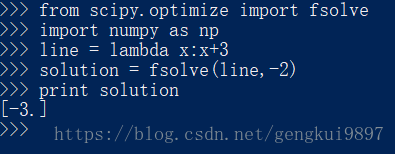
例如:线性函数求解
from scipy.optimize import fsolve
import numpy as np
line = lambda x:x+3
solution = fsolve(line,-2)
print solution
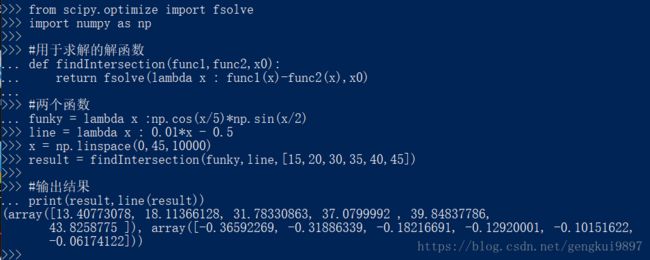
例如:求函数交叉点
from scipy.optimize import fsolve
import numpy as np
#用于求解的解函数
def findIntersection(func1,func2,x0):
return fsolve(lambda x : func1(x)-func2(x),x0)
#两个函数
funky = lambda x :np.cos(x/5)*np.sin(x/2)
line = lambda x : 0.01*x - 0.5
x = np.linspace(0,45,10000)
result = findIntersection(funky,line,[15,20,30,35,40,45])
#输出结果
print(result,line(result))
2.插值
(1)interp1d
例如:正弦函数插值
import numpy as np
from scipy.interpolate import interp1d
#创建待插值的数据
x = np.linspace(0,10*np.pi,20)
y = np.cos(x)
#分别用linear和quadratic插值
fl = interp1d(x,y,kind='linear')
fq = interp1d(x,y,kind='quadratic')
xint = np.linspace(x.min(),x.max(),1000)
yintl = fl(xint)
yintq = fq(xint)
(2)UnivariateSpline
例如:噪声数据插值
import numpy as np
from scipy.interpolate import UnivariateSpline
#创建含噪声的待插值数据
sample = 30
x = np.linspace(1,10*np.pi,sample)
y = np.cos(x) + np.log10(x) + np.random.randn(sample)/10
#插值,参数s为smoothing factor
f = UnivariateSpline(x,y,s=1)
xint = np.linspace(x.min(),x.max(),1000)
yint = f(xint)
(3)griddata
例如:利用插值重构图片
import numpy as np
from scipy.interpolate import griddata
#定义一个函数
ripple = lambda x,y : np.sqrt(x**2+y**2) + np.sin(x**2,y**2)
#生成grid数据,复数定义了生成grid数据的step,若无该复数则step为5
grid_x,grid_y = np.mgrid[0:5:1000j,0:5:1000j]
#生成待插值的数据样本
xy = np.random.rand(1000,2)
sample = ripple(xy[:,0]*5,xy[:,1]*5)
#用cubic方法插值
grid_z0 = griddata(xy*5,sample,(grid_x,grid_y),method='cubic')
(4)SmoothBivariateSpline
例如:利用插值重构图片
import numpy as np
from scipy.interpolate import SmoothBivariateSpline as SBS
#定义函数
ripple = lambda x,y : np.sqrt(x**2+y**2)+np.sin(x**2+y**2)
#生成待插值样本
xy=np.random.rand(1000,2)
x,y = xy[:,0],xy[:,1]
sample = ripple(xy[:,0]*5,xy[:,1]*5)
#插值
fit = SBS(x*5,y*5,sample,s=0.01,kx=4,ky=4)
interp = fit(np.linspace(0,5,1000),np.linspace(0,5,1000))
3.积分
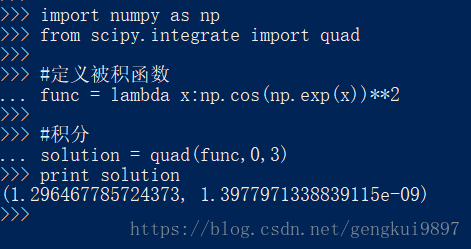
(1)解析积分
import numpy as np
from scipy.integrate import quad
#定义被积函数
func = lambda x:np.cos(np.exp(x))**2
#积分
solution = quad(func,0,3)
print solution
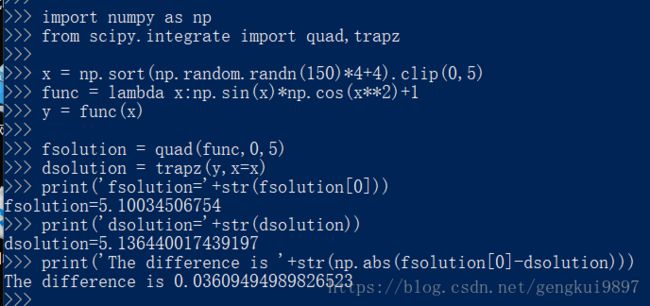
(2)数值积分
import numpy as np
from scipy.integrate import quad,trapz
x = np.sort(np.random.randn(150)*4+4).clip(0,5)
func = lambda x:np.sin(x)*np.cos(x**2)+1
y = func(x)
fsolution = quad(func,0,5)
dsolution = trapz(y,x=x)
print('fsolution='+str(fsolution[0]))
print('dsolution='+str(dsolution))
print('The difference is '+str(np.abs(fsolution[0]-dsolution)))
4.统计
SciPy中包括mean,std,median,argmax及argmin等在内的基本统计函数,而且numpy.arrays类型中内置了大部分统计函数,以便易于使用。
import numpy as np
elements x = np.random.randn(1000)
mean = x.mean() #均值
std = x.std() #标准差
var = x.var() #方差
SciPy中还包括了各种分布、函数等工具。连续和离散分布SciPy的scipy.stats包中包含了大概80种连续分布和10种离散分布。
例如:概率密度函数(PDFs)
import numpy as np
from scipy.stats import norm
#创建样本区间
x = np.linspace(-5,5,1000)
#设置正态分布参数,loc为均值,scale为标准差
dist = norm(loc=0,scale=1)
#得到正态分布的PDF和CDF
pdf = dist.pdf(x)
cdf = dist.cdf(x)
#根据分布生成500个随机数
sample = dist.rvs(500)
例如:几何分布概率分布函数(PMF)
import numpy as np
from scipy.stats import geom
#设置几何分布参数
p = 0.5
dist = geom(p)
#设置样本空间
x = np.linspace(0,5,1000)
#得到几何分布的PMF和CDF
pmf = dist.pmf(x)
cdf = dist.cdf(x)
#生成500个随机数
sample = dist.rvs(500)
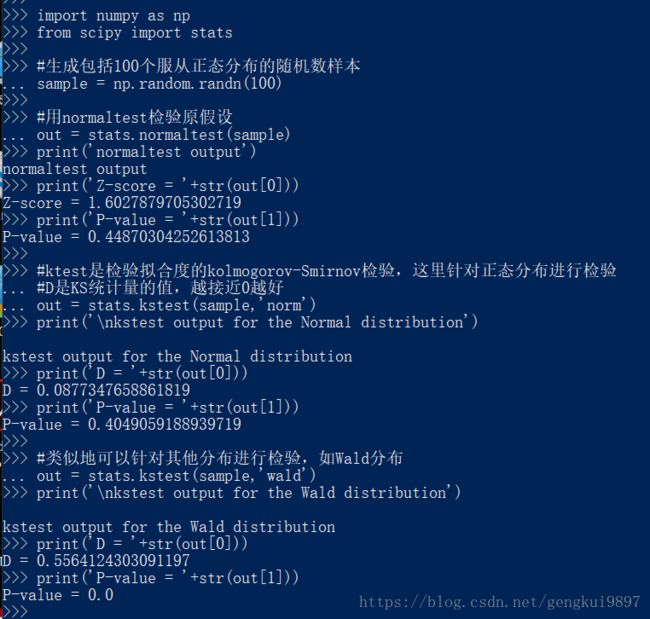
例如:样本分布检验
import numpy as np
from scipy import stats
#生成包括100个服从正态分布的随机数样本
sample = np.random.randn(100)
#用normaltest检验原假设
out = stats.normaltest(sample)
print('normaltest output')
print('Z-score = '+str(out[0]))
print('P-value = '+str(out[1]))
#ktest是检验拟合度的kolmogorov-Smirnov检验,这里针对正态分布进行检验
#D是KS统计量的值,越接近0越好
out = stats.kstest(sample,'norm')
print('\nkstest output for the Normal distribution')
print('D = '+str(out[0]))
print('P-value = '+str(out[1]))
#类似地可以针对其他分布进行检验,如Wald分布
out = stats.kstest(sample,'wald')
print('\nkstest output for the Wald distribution')
print('D = '+str(out[0]))
print('P-value = '+str(out[1]))
5.空间和聚类分析
(1)矢量量化
矢量量化是信号处理、数据压缩和聚类等领域通用的术语。这里仅关注其在聚类中的应用
例如:k均值聚类
import numpy as np
from scipy.cluster import vq
#生成数据
c1 = np.random.randn(100,2)+5
c2 = np.random.randn(30,2)-5
c3 = np.random.randn(50,2)
#将所有数据放入一个180*2的数组
data = np.vstack([c1,c2,c3])
#利用k均值方法计算聚类的质心和方差
centroids,variance = vq.kmeans(data,3)
#变量identified中存放关于聚类的信息
identified,distance = vq.vq(data,centroids)
#获得各类别的数据
vqc1 = data[identified == 0]
vqc2 = data[identified == 1]
vqc3 = data[identified == 2]
(2)层次聚类
层次聚类是一种重要的聚类方法,但其输出结果比较复杂,不能像k均值那样给出清晰的聚类结果。
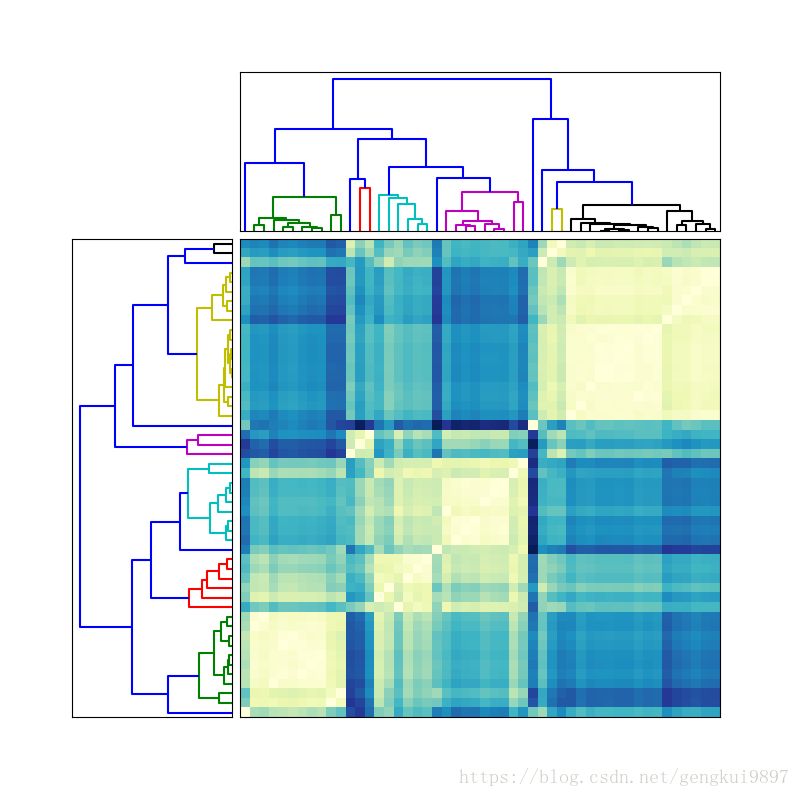
例如:输入一个距离矩阵,输出一个树状图
#coding:utf-8
import numpy as np
import matplotlib.pyplot as mpl
from scipy.spatial.distance import pdist,squareform
import scipy.cluster.hierarchy as hy
#用于生成聚类数据的函数
def clusters(number=20,cnumber=5,csize=10):
#聚类服从高斯分布
rnum = np.random.rand(cnumber,2)
rn = rnum[:,0]*number
rn = rn.astype(int)
rn[np.where(rn<5)] = 5
rn[np.where(rn>number/2.)] = round(number/2.0)
ra = rnum[:,1]*2.9
ra[np.where(ra<1.5)] = 1.5
cls = np.random.randn(number,3)*csize
rxyz = np.random.randn(cnumber-1,3)
for i in xrange(cnumber-1):
tmp = np.random.randn(rn[i+1],3)
x = tmp[:,0]+(rxyz[i,0]*csize)
y = tmp[:,1]+(rxyz[i,1]*csize)
z = tmp[:,2]+(rxyz[i,2]*csize)
tmp = np.column_stack([x,y,z])
cls = np.vstack([cls,tmp])
return cls
#创建待聚类数据及距离矩阵
cls = clusters()
D = pdist(cls[:,0:2])
D = squareform(D)
#绘制左侧树状图
fig = mpl.figure(figsize=(8,8))
ax1 = fig.add_axes([0.09,0.1,0.2,0.6])
Y1 = hy.linkage(D,method='complete')
cutoff = 0.3 * np.max(Y1[:,2])
Z1 = hy.dendrogram(Y1,orientation='left',color_threshold=cutoff)
ax1.xaxis.set_visible(False)
ax1.yaxis.set_visible(False)
#绘制顶部树状图
ax2 = fig.add_axes([0.3,0.71,0.6,0.2])
Y2 = hy.linkage(D,method='average')
cutoff = 0.3 * np.max(Y2[:,2])
Z2 = hy.dendrogram(Y2,color_threshold=cutoff)
ax2.xaxis.set_visible(False)
ax2.yaxis.set_visible(False)
#显示距离矩阵
ax3 = fig.add_axes([0.3,0.1,0.6,0.6])
idx1 = Z1['leaves']
idx2 = Z2['leaves']
D = D[idx1,:]
D = D[:,idx2]
ax3.matshow(D,aspect='auto',origin='lower',cmap=mpl.cm.YlGnBu)
ax3.xaxis.set_visible(False)
ax3.yaxis.set_visible(False)
#保存图片,显示图片
fig.savefig('cluster_hy_f01.pdf',bbox='tight')
mpl.show()
在上图虽然计算了数据点之间的距离,但是还是难以将各类·区分开。函数fcluster可以根据阈值来区分各类,其输出结果依赖于linkage函数所采用的方法,如complete或者single等,它的第二个参数既是阈值。dendrogram函数中默认的阈值是0.7*np.max(Y[:,2]),这里还使用0.3。
例如:
#coding:utf-8
import numpy as np
import matplotlib.pyplot as mpl
from scipy.spatial.distance import pdist,squareform
import scipy.cluster.hierarchy as hy
#得到不同类别数据点的坐标
def group(data,index):
number = np.unique(index)
groups = []
for i in number:
groups.append(data[index == i])
return groups
#用于生成聚类数据的函数
def clusters(number=20,cnumber=5,csize=10):
#聚类服从高斯分布
rnum = np.random.rand(cnumber,2)
rn = rnum[:,0]*number
rn = rn.astype(int)
rn[np.where(rn<5)] = 5
rn[np.where(rn>number/2.)] = round(number/2.0)
ra = rnum[:,1]*2.9
ra[np.where(ra<1.5)] = 1.5
cls = np.random.randn(number,3)*csize
rxyz = np.random.randn(cnumber-1,3)
for i in xrange(cnumber-1):
tmp = np.random.randn(rn[i+1],3)
x = tmp[:,0]+(rxyz[i,0]*csize)
y = tmp[:,1]+(rxyz[i,1]*csize)
z = tmp[:,2]+(rxyz[i,2]*csize)
tmp = np.column_stack([x,y,z])
cls = np.vstack([cls,tmp])
return cls
#创建数据
cls = clusters()
#计算linkage矩阵
Y = hy.linkage(cls[:,0:2],method='complete')
#从层次数据结构中,用fcluster函数将层次结构的数据转为flat cluster
cutoff = 0.3 * np.max(Y[:,2])
index = hy.fcluster(Y,cutoff,'distance')
#使用groups函数将数据划分类别
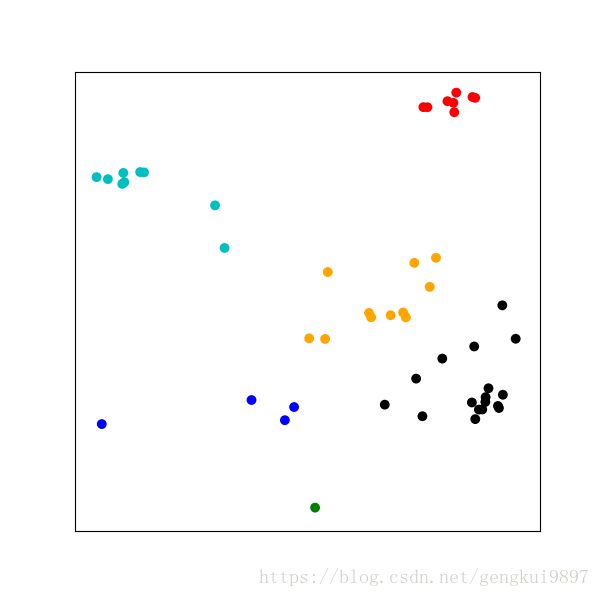
groups = group(cls,index)
#绘制数据点
fig = mpl.figure(figsize=(6,6))
ax = fig.add_subplot(111)
colors = ['r','c','b','g','orange','k','y','gray']
for i,g in enumerate(groups):
i = np.mod(i,len(colors))
ax.scatter(g[:,0],g[:,1],c=colors[i],edgecolor='none',s=50)
ax.xaxis.set_visible(False)
ax.yaxis.set_visible(False)
fig.savefig('cluster_hy_f02.pdf',bbox='tight')
mpl.show()
6.稀疏矩阵
NumPy处理10^6级别的数据没有什么大问题·,当数据量达到10^7级别时速度开始变慢,内存受到限制。当处理超大规模数据集,比如10^10级别,且数据中包含大量的0时,可采用稀疏矩阵提高速度和效率
提示:使用data.nbytes可查看数据可占空间大小
例如:矩阵与稀疏矩阵运算对比
# coding:utf-8
import numpy as np
from scipy.sparse.linalg import eigsh
from scipy.linalg import eigh
import scipy.sparse
import time
N = 3000
#创建随机稀疏矩阵
m = scipy.sparse.rand(N,N)
#创建包含相同数据的数组
a = m.toarray()
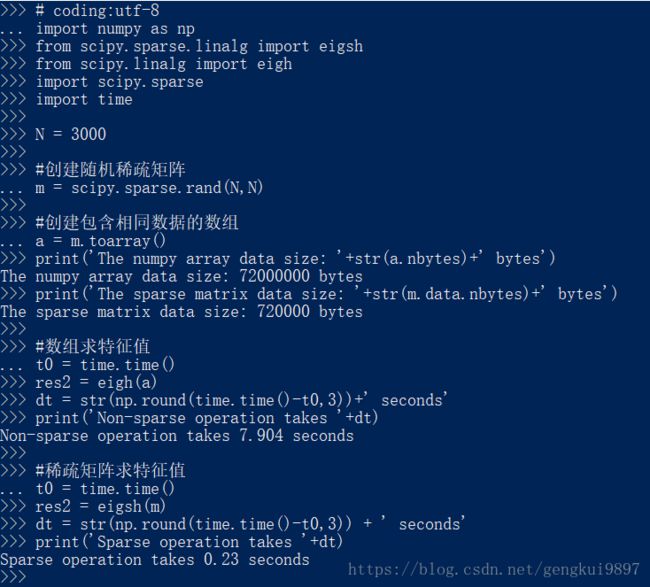
print('The numpy array data size: '+str(a.nbytes)+' bytes')
print('The sparse matrix data size: '+str(m.data.nbytes)+' bytes')
#数组求特征值
t0 = time.time()
res2 = eigh(a)
dt = str(np.round(time.time()-t0,3))+' seconds'
print('Non-sparse operation takes '+dt)
#稀疏矩阵求特征值
t0 = time.time()
res2 = eigsh(m)
dt = str(np.round(time.time()-t0,3)) + ' seconds'
print('Sparse operation takes '+dt)