Python数据结构之复杂数据结构
目录
- Trie树的基础知识
- 实现trie树 (LeetCode 208)
- 添加与查找单词 (LeetCode 211)
- 并查集的基础知识
- 朋友圈 (LeetCode 547)
- 线段树的基础知识
- 区域和查询(LeetCode 307)
- 逆序数 (LeetCode 315)
1. Trie树的基础知识
参考:https://blog.csdn.net/handsomekang/article/details/41446319
trie,又称前缀树或字典树. 它利用字符串的公共前缀来节约存储空间.
定义
Trie树中每个单词都是通过character by character方法进行存储,相同前缀单词共享前缀节点.
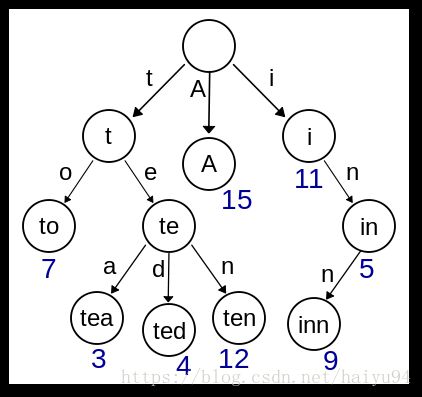
可以看到,每条路径组成一个单词.上面这颗树存了to/tea/ted/ten/inn这些词.性质
(1)根节点不包含字符,除根节点外的每个节点只包含一个字符。
(2)从根节点到某一个节点,路径上经过的字符连接起来,为该节点对应的字符串。
(3)每个节点的所有子节点包含的字符串不相同。- 应用
- 词频统计
比直接用hash节省空间 - 搜索提示
输入前缀的时候提示可以构成的词 - 作为辅助结构
如后缀树,AC自动机等的辅助结构
- 词频统计
- 实现
虽然python没有指针,但是可以用嵌套字典来实现树结构.对于非ascii的单词,统一用unicode编码来插入与搜索.
2. 实现trie树 (LeetCode 208 Implement Trie (Prefix Tree))
2.1题目
Implement a trie with insert, search, and startsWith methods.
Note:
You may assume that all inputs are consist of lowercase letters a-z.
2.2思路
is_word:判断当前单词是否结束
children:表示当前字母
2.3代码
class TriNode(object):
def __init__(self):
self.is_word = False
self.children = [None] *26
class Trie(object):
def __init__(self):
""" Initialize your data structure here. """
self.root = TriNode()
def insert(self, word):
""" Inserts a word into the trie. :type word: str :rtype: void """
p = self.root
n = len(word)
for i in range(n):
if p.children[ord(word[i]) - ord('a')] == None:
new_node = TriNode()
if i == n-1:
new_node.is_word = True
p.children[ord(word[i]) - ord('a')] = new_node
p = new_node
else:
p = p.children[ord(word[i]) - ord('a')]
if i == n-1:
p.is_word = True
return
def search(self, word):
""" Returns if the word is in the trie. :type word: str :rtype: bool """
p = self.root
for c in word:
p = p.children[ord(c) - ord('a')]
if p is None:
return False
if p.is_word:
return True
else:
return False
def startsWith(self, prefix):
""" Returns if there is any word in the trie that starts with the given prefix. :type prefix: str :rtype: bool """
p = self.root
for c in prefix:
p = p.children[ord(c) - ord('a')]
if p is None:
return False
return True3. 添加与查找单词 (LeetCode 211)
3.1题目
Design a data structure that supports the following two operations:
void addWord(word)
bool search(word)
search(word) can search a literal word or a regular expression string containing only letters a-z or .. A . means it can represent any one letter.
For example:
addWord("bad")
addWord("dad")
addWord("mad")
search("pad") -> false
search("bad") -> true
search(".ad") -> true
search("b..") -> true
3.2思路
和上一题思路类似
3.3代码
class TriNode(object):
def __init__(self):
self.is_word = False
self.children = [None] *26
class WordDictionary(object):
def __init__(self):
""" Initialize your data structure here. """
self.root = TriNode()
def addWord(self, word):
""" Adds a word into the data structure. :type word: str :rtype: void """
p = self.root
n = len(word)
for i in range(n):
if p.children[ord(word[i]) - ord('a')] == None:
new_node = TriNode()
if i == n - 1:
new_node.is_word = True
p.children[ord(word[i]) - ord('a')] = new_node
p = new_node
else:
p = p.children[ord(word[i]) - ord('a')]
if i == n - 1:
p.is_word = True
def search(self, word):
""" Returns if the word is in the data structure. A word could contain the dot character '.' to represent any one letter. :type word: str :rtype: bool """
p = self.root
return self.match(word, p, 0)
def match(self, word, p, i):
if i == len(word):
return p.is_word
if word[i] == '.':
for child in p.children:
if child != None and self.match(word, child, i + 1):
return True
return False
else:
if p.children[ord(word[i]) - ord('a')] != None and self.match(word, p.children[ord(word[i]) - ord('a')], i + 1):
return True
else:
return False4. 并查集的基础知识
参考:https://segmentfault.com/a/1190000013805875
并查集,一种树型的数据结构,处理一些不相交集合的合并及查询问题。
并查集有三种基本操作,获得根节点,判断两节点是否连通,以及将两不连通的节点相连(相当于将两节点各自的集合合并)
用UnionFind类来表示一个并查集,在构造函数中,初始化一个数组parent,parent[i]表示的含义为,索引为i的节点,它的直接父节点为parent[i]。初始化时各个节点都不相连,因此初始化parent[i]=i,让自己成为自己的父节点,从而实现各节点不互连。
def __init__(self, n):
self.parent = list(range(n))由于parent[i]仅表示自己的直接父节点,查询两个节点是否相交需要比较它们的根节点是否相同。因此要封装一个查询自己根节点的方法。
通过对union操作的改良可以防止树的高度过高。我们还可以对get_root操作本身进行优化。
当前每次执行get_root时,需要一层一层的找到自己的父节点,很费时。由于根节点没有父节点,并且如果一个节点没有父节点,那么它的父节点就是自己,因此可以说只有根节点的父节点是自己本身。现在我们加上一个判断,判断当前节点的父节点是否为根节点,如果不为根节点,就递归地将自己的父节点设置为根节点,最后返回自己的父节点。
def get_root(self, i):
if self.parent[i] != self.parent[self.parent[i]]:
self.parent[i] = self.get_root(self.parent[i])
return self.parent[i]接下来可以通过来比较根节点是否相同来判断两节点是否连通。
def is_connected(self, i, j):
return self.get_root(i) == self.get_root(j)当要连通两个节点时,我们要将其中一个节点的根节点的parent,设置为另一个节点的根节点。注意,连通两个节点并非仅仅让两节点自身相连,实际上是让它们所属的集合实现合并。
由于调用get_root时需要通过不断找自己的直接父节点,来寻找根节点,如果这棵树的层级过深,会导致性能受到严重影响。因此我们需要在union时,尽可能的减小合并后的树的高度。
在构造函数中新建一个数组rank,rank[i]表示节点i所在的集合的树的高度。
因此,当合并树时,分别获得节点i和节点j的root i_root和j_root之后,我们通过访问rank[i_root]和rank[j_root]来比较两棵树的高度,将高度较小的那棵连到高度较高的那棵上。如果高度相等,则可以随便,并将rank值加一。
def union(self, i, j):
i_root = self.get_root(i)
j_root = self.get_root(j)
if self.rank[i_root] == self.rank[j_root]:
self.parent[i_root] = j_root
self.rank[j_root] += 1
elif self.rank[i_root] > self.rank[j_root]:
self.parent[j_root] = i_root
else:
self.parent[i_root] = j_root5. 朋友圈 (LeetCode 547)
5.1题目
There are N students in a class. Some of them are friends, while some are not. Their friendship is transitive in nature. For example, if A is a direct friend of B, and B is a direct friend of C, then A is an indirect friend of C. And we defined a friend circle is a group of students who are direct or indirect friends.
Given a N*N matrix M representing the friend relationship between students in the class. If M[i][j] = 1, then the ith and jth students are direct friends with each other, otherwise not. And you have to output the total number of friend circles among all the students.
Example 1:
Input:
[[1,1,0],
[1,1,0],
[0,0,1]]
Output: 2
Explanation:The 0th and 1st students are direct friends, so they are in a friend circle.
The 2nd student himself is in a friend circle. So return 2.
Example 2:
Input:
[[1,1,0],
[1,1,1],
[0,1,1]]
Output: 1
Explanation:The 0th and 1st students are direct friends, the 1st and 2nd students are direct friends,
so the 0th and 2nd students are indirect friends. All of them are in the same friend circle, so return 1.
5.2思路
使用并查集
5.3代码
class Solution(object):
def findCircleNum(self, M):
""" :type M: List[List[int]] :rtype: int """
ds = DisjointSet()
for i in range(len(M)):
ds.make_set(i)
for i in range(len(M)):
for j in range(len(M)):
if M[i][j] == 1:
ds.union(i, j)
return ds.num_sets
class Node(object):
def __init__(self, data, parent=None, rank=0):
self.data = data
self.parent = parent
self.rank = rank
class DisjointSet(object):
def __init__(self):
self.map = {}
self.num_sets = 0
def make_set(self, data):
node = Node(data)
node.parent = node
self.map[data] = node
self.num_sets += 1
def union(self, data1, data2):
node1 = self.map[data1]
node2 = self.map[data2]
parent1 = self.find_set_util(node1)
parent2 = self.find_set_util(node2)
if parent1.data == parent2.data:
return
if parent1.rank >= parent2.rank:
if parent1.rank == parent2.rank:
parent1.rank += 1
parent2.parent = parent1
else:
parent1.parent = parent2
self.num_sets -= 1
def find_set(self, data):
return self.find_set_util(self.map[data])
def find_set_util(self, node):
parent = node.parent
if parent == node:
return parent
node.parent = self.find_set_util(node.parent) # path compression
return node.parent6. 线段树的基础知识
线段树是一种二叉搜索树,与区间树相似,它将一个区间划分成一些单元区间,每个单元区间对应线段树中的一个叶结点。
对于线段树中的每一个非叶子节点[a,b],它的左儿子表示的区间为[a,(a+b)/2],右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树,最后的子节点数目为N,即整个线段区间的长度。
使用线段树可以快速的查找某一个节点在若干条线段中出现的次数,时间复杂度为O(logN)。而未优化的空间复杂度为2N,因此有时需要离散化让空间压缩。
7. 区域和查询(LeetCode 307Range Sum Query - Mutable)
7.1题目
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.
The update(i, val) function modifies nums by updating the element at index i to val.
Example:
Given nums = [1, 3, 5]
sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8
Note:
The array is only modifiable by the update function.
You may assume the number of calls to update and sumRange function is distributed evenly.
7.2思路
这一题感觉朴素做法就可以了呀==
7.3代码
class NumArray(object):
def __init__(self, nums):
"""
:type nums: List[int]
"""
self.nums = nums
def update(self, i, val):
"""
:type i: int
:type val: int
:rtype: void
"""
self.nums[i] = val
def sumRange(self, i, j):
"""
:type i: int
:type j: int
:rtype: int
"""
return sum(self.nums[i:j+1])
8. 逆序数 (LeetCode 315315. Count of Smaller Numbers After Self)
8.1题目
You are given an integer array nums and you have to return a new counts array. The counts array has the property where counts[i] is the number of smaller elements to the right of nums[i].
Example:
Given nums = [5, 2, 6, 1]
To the right of 5 there are 2 smaller elements (2 and 1).
To the right of 2 there is only 1 smaller element (1).
To the right of 6 there is 1 smaller element (1).
To the right of 1 there is 0 smaller element.
Return the array [2, 1, 1, 0].
8.2思路
使用二叉搜索树做
8.3代码
class BinarySearchTreeNode(object):
def __init__(self, val):
self.val = val
self.left = None
self.right = None
self.count = 1
self.leftTreeSize = 0
class BinarySearchTree(object):
def __init__(self):
self.root = None
def insert(self, val, root):
if not root:
self.root = BinarySearchTreeNode(val)
return 0
if val == root.val:
root.count += 1
return root.leftTreeSize
if val < root.val:
root.leftTreeSize += 1
if not root.left:
root.left = BinarySearchTreeNode(val)
return 0
return self.insert(val, root.left)
if not root.right:
root.right = BinarySearchTreeNode(val)
return root.count + root.leftTreeSize
return root.count + root.leftTreeSize + self.insert(
val, root.right)
class Solution(object):
def countSmaller(self, nums):
""" :type nums: List[int] :rtype: List[int] """
tree = BinarySearchTree()
return [
tree.insert(nums[i], tree.root)
for i in xrange(len(nums) - 1, -1, -1)
][::-1]