【机器学习】Logistic回归算法学习笔记

假设现在有一些数据点，我们用一条直线（或者曲线）对这些点进行拟合，这个拟合过程就称作回归。

利用Logistic回归进行分类的主要思想是：根据现有数据对分类边界线建立回归公式，以此进行分类，训练分类器时的做法就是寻找最佳拟合参数。

• 优点：计算代价不高，易于理解和实现。
• 缺点：容易欠拟合，分类精度可能不高。
• 适用数据类型：数值型和标称型数据。

一、Sigmoid函数

我们想要的分类函数应该是能够接受所有的输入然后预测出类别。Sigmoid函数就是这样一个函数。

当x为0时，Sigmoid函数值为0.5。随着x的增大，对应的Sigmoid值将逼近于1.而随着x的减小，Sigmoid值将逼近于0。

Sigmoid函数的输入记为z，由下面的公式得出：

其中，x是分类器的输入数据，w就是我们需要寻找的分类器的最佳参数。

二、梯度上升法

为了寻找分类器的最佳参数，这里用到的最优化方法是梯度上升法。

梯度上升法的思想是：要找到某个函数的最大值，最好的方法是沿着该函数的梯度方向寻找。

一直迭代上述公式，直至达到某个停止条件为止。

梯度上升法的伪代码如下：

每个回归系数初始化为1
重复R次：
    计算整个数据集的梯度
    使用alpha x gradient更新回归系数的向量
    返回回归系数

下面是一个Logistic回归梯度上升优化算法的例子。

首先，从文本文件中读取输入数据：

from numpy import *

def loadDataSet():
    dataMat = []
    labelMat = []
    fr = open('testSet.txt')
    for line in fr.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat, labelMat

定义Sigmoid函数：

def sigmoid(inX):
    return 1.0/(1+exp(-inX))

梯度上升优化算法：

def gradAscent(dataMatIn, classLabels):
    dataMatrix = mat(dataMatIn)
    labelMat = mat(classLabels).transpose()
    m ,n = shape(dataMatrix)
    alpha = 0.001
    maxCycles = 500
    weights = ones((n, 1))
    for k in range(maxCycles):
        h = sigmoid(dataMatrix*weights)
        error = (labelMat - h)
        weights = weights + alpha * dataMatrix.transpose() * error
    return weights

调用函数，打印出计算得到的优化参数：

dataArr, labelMat = loadDataSet()
weights = gradAscent(dataArr, labelMat)
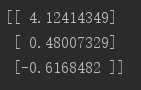
print(weights)

输出：

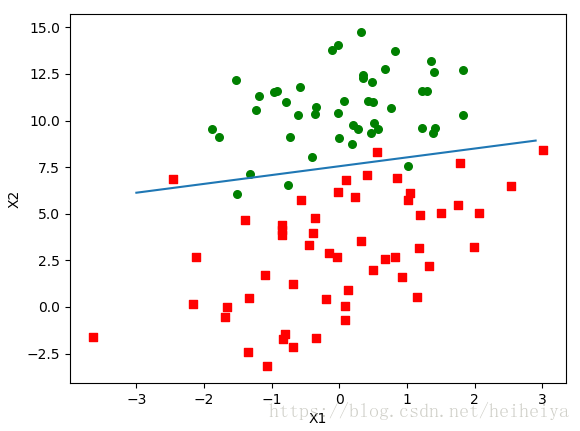
但是这样看起来没有直观的感受，下面来可视化分类效果。

def plotBestFit(weights):
    import matplotlib.pyplot as plt
    dataMat, labelMat = loadDataSet()
    dataArr = array(dataMat)
    n = shape(dataArr)[0]
    xcord1 = []
    ycord1 = []
    xcord2 = []
    ycord2 = []
    for i in range(n):
        if int(labelMat[i]) == 1:
            xcord1.append(dataArr[i, 1])
            ycord1.append(dataArr[i, 2])
        else:
            xcord2.append(dataArr[i, 1])
            ycord2.append(dataArr[i, 2])
    fig = plt.figure()
    ax = fig.add_subplot(111)
    ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
    ax.scatter(xcord2, ycord2, s=30, c='green')
    x = arange(-3.0, 3.0, 0.1)
    y = (-weights[0]-weights[1]*x)/weights[2]
    ax.plot(x, y)
    plt.xlabel('X1')
    plt.ylabel('X2')
    plt.show()

plotBestFit(weights.getA())

三、随机梯度上升法

梯度上升法的一个缺点就是每次更新回归系数时都需要遍历整个数据集，这在处理小数据集时尚可，但数据集一旦很大那么计算复杂度就太高了。

随机梯度上升法就是对它的一种改进，一次只使用一个样本点来更新回归系数。其伪代码如下：

所有回归系数初始化为1
    对数据集中每个样本
    计算该样本的梯度
    使用alpha × gradient更新回归系数值
返回回归系数值

def stocGradAscent0(dataMatrix, classLabels):
    m, n = shape(dataMatrix)
    alpha = 0.01
    maxCycles = 200
    weights = ones(n)
    for k in range(maxCycles):
        for i in range(m):
            h = sigmoid(sum(dataMatrix[i]*weights))
            error = classLabels[i] - h
            weights = weights + alpha * error * dataMatrix[i]
    return weights

调用

weights2 = stocGradAscent0(array(dataArr), labelMat)
plotBestFit(weights2)

四、改进的随机梯度上升法

但是，在训练过程中，由于有一些不能正确分类点的存在，导致系数剧烈改变，波动很大。因此对随机梯度上升法做一些改动。

def stocGradAscent1(dataMatrix, classLabels, numIter=150):
    m, n = shape(dataMatrix)
    weights = ones(n)
    for j in range(numIter):
        dataIndex = list(range(m))
        for i in range(m):
            alpha = 4/(1.0+j+i) + 0.01
            randIndex = int(random.uniform(0, len(dataIndex)))
            h = sigmoid(sum(dataMatrix[randIndex]*weights))
            error = classLabels[randIndex] - h
            weights = weights + alpha * error * dataMatrix[randIndex]
            del(dataIndex[randIndex])
    return weights

 首先，alpha在每次迭代时都会改变。其次是通过随机选取样本来更新回归系数。

weights3 = stocGradAscent1(array(dataArr), labelMat)
plotBestFit(weights3)