linkedList源码分析jdk1.8
前言:
上篇文章我们分析了常见的ArrayList源码,它的内部是由一个数组来实现的。那么今天,我们来分析另一个常见的类LinkedList。
public class LinkedList
extends AbstractSequentialList
implements List, Deque, Cloneable, java.io.Serializable
{
transient int size = 0;
/**
* Pointer to first node.
* Invariant: (first == null && last == null) ||
* (first.prev == null && first.item != null)
*/
transient Node first;
/**
* Pointer to last node.
* Invariant: (first == null && last == null) ||
* (last.next == null && last.item != null)
*/
transient Node last;
从LinkedList这个类名我们就猜出,这个List内部可能是由链表来实现,我们后面来验证一下。它实现了Deque接口,因此可以知道,LinkedList也可以作为队列来进行使用。同时也实现了Serializable接口,说明可以对它进行序列化,反序列化来传递,获取数据等等。
1、成员变量
首先是一个int类型的size,这个我们在ArrayList中也介绍过。这个是一个表明List有多少个元素。然后是一个Node类型的first变量,从注释我们看出指向头结点的变量(用C,C++解释称之为指针,也许用C语言的方式更好解释)。后面的last变量也很好理解,它指向最后结点。我们跟进Node类去看看源码:
private static class Node {
E item;
Node next;
Node prev;
Node(Node prev, E element, Node next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
这是一个LinkedList的内部类,还是比较简单的。首先一个泛型的item变量,用来存储数据,然后有一个指向下一个结点的next指针,前一个结点的prev指针。
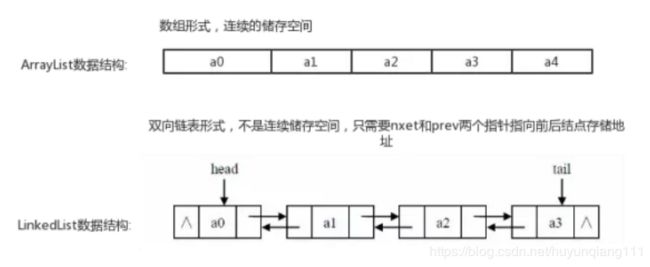
至此我们其实就可以得出结论,LinkedList果然名不虚传,内部就是由链表的形式实现。它并没有用数组来存储数据元素,而是由一个个Node类型结点来储存数据,然后每个Node结点通过指向前后结点的next和prev指针将整个List串联起来。我们来画张简单图来看看ArrayList和LinkedList的基本区别:
正是这样的区别,从而导致了两者不同的效率问题。如果我们对一个ArrayList频繁的增加数据,那么内部的数组就会不断扩容创建新的数组然后把旧数据复制到新数组返回。插入数据或者删除其中一个数据,又要把所有数据后移或者前移。这样的操作效率很低下的,为了一个数据处理了其他数据。
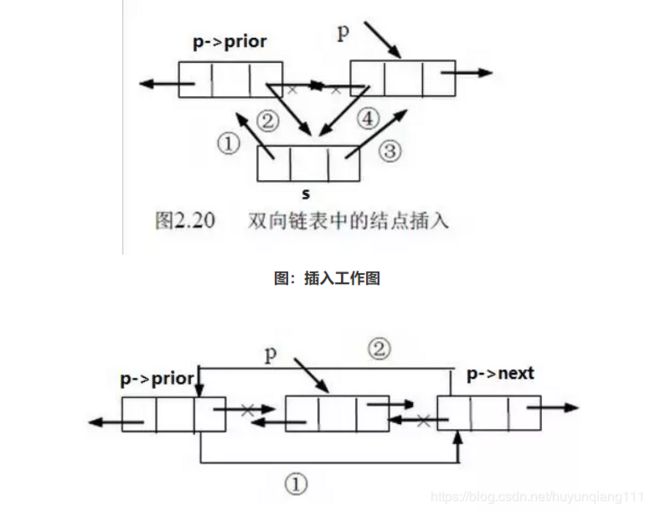
而LinkedList不同,插入只需要将要插入位置的前结点的next指针指向新的数据结点(如下图插入工作图的2),将插入结点的prev指向前指针(如1处),将next指向下一个结点(如3处),将之前的后结点的prev指针指向插入指针(如4处)删除也是如下删除工作图,就不再讲述。这样的话只需要几步操作就完成了处理,无需移动大量数据。效率非常高。
2、构造方法:
/**
* Constructs an empty list.
*/
public LinkedList() {
}
/**
* Constructs a list containing the elements of the specified
* collection, in the order they are returned by the collection's
* iterator.
*
* @param c the collection whose elements are to be placed into this list
* @throws NullPointerException if the specified collection is null
*/
public LinkedList(Collection c) {
this();
addAll(c);
}
第一个构造方法是空实现,因为内部是链表,无需像ArrayLsi一样t实例化数组。
我们来看看第二个构造方法,传入参数为一个集合,主要是调用了addAll()方法,我们来看看:
public boolean addAll(Collection c) {
return addAll(size, c);
}
public boolean addAll(int index, Collection c) {
checkPositionIndex(index);
Object[] a = c.toArray();
int numNew = a.length;
if (numNew == 0)
return false;
Node pred, succ;
if (index == size) {
succ = null;
pred = last;
} else {
succ = node(index);
pred = succ.prev;
}
for (Object o : a) {
@SuppressWarnings("unchecked") E e = (E) o;
Node newNode = new Node<>(pred, e, null);
if (pred == null)
first = newNode;
else
pred.next = newNode;
pred = newNode;
}
if (succ == null) {
last = pred;
} else {
pred.next = succ;
succ.prev = pred;
}
size += numNew;
modCount++;
return true;
}
第一个addAll()方法将size传入,其实就是从原有List的末尾开始添加传入的数据,而这里size为0。所以就是从头开始添加数据。我们仔细分析第二个addAll()方法。
我们拆开来分析:
private void checkPositionIndex(int index) {
if (!isPositionIndex(index))
throw new IndexOutOfBoundsException(outOfBoundsMsg(index));
}
//isPositionIndex
private boolean isPositionIndex(int index) {
return index >= 0 && index <= size;
}
首先checkPositionIndex()方法来判断传入的index是否大于0并且小于size。
然后将传入的集合首先转换为数组。然后判断数组长度是否为0,如果是0,表示没有添加的数据,直接返回。
如果不是,那么定义两个结点succ和pred。个人理解succ表示要插入的index下标的结点,pred表示succ结点的前结点。然后判断index是否等于size,而我们在构造方法中传入的index就等于size,所以表示从链表的末尾开始添加数据。即succ为null(因为下标从0开始,所以最后一个数据下标为size - 1),pred为last最后一个结点。如果index不等于size,那么找到index处的结点赋值给succ,pred等于succ的前结点。
到这里就已经把预处理工作完成了。接下来就是添加数据过程。首先是一个for循环遍历a数组。每个对象(也就是数据)都生成一个结点。然后将新结点的前指针指向pred结点。如果pred为空(这种情况就是链表为空,没有一个结点),那么这个新结点就是链表的表头。如果pred不为空,那么将pred的后指针指向这个新结点。这样就将pred结点和新结点串联起来。然后pred往后移一个结点,指向新结点。这样就不断的将所有新数据插入到指点位置往后。
到这里就已经把预处理工作完成了。接下来就是添加数据过程。首先是一个for循环遍历a数组。每个对象(也就是数据)都生成一个结点。然后将新结点的前指针指向pred结点。如果pred为空(这种情况就是链表为空,没有一个结点),那么这个新结点就是链表的表头。如果pred不为空,那么将pred的后指针指向这个新结点。这样就将pred结点和新结点串联起来。然后pred往后移一个结点,指向新结点。这样就不断的将所有新数据插入到指点位置往后。
for循环后,会判断succ是否为空(即我们插入位置的旧结点是否为空)。如果为空,表明我们是插入到链表的末尾的,那么就无需将旧结点的后结点的prev指针修改(因为根本没后结点),直接将last指向pred(因为在for循环中pred会指向新数据集合的最后一个数据)即可。如果succ不为空,表示我们是在链表的中间插入数据的。因此就要将新数据集合的最后一个数据结点的next后指针指向我们插入位置的结点。然后将未插入前的index处的结点的前结点修改为指向新插入的最后一个数据结点即pred。
最后将数据数量加上新插入的数据数量,修改数据结构次数自加1即可。
至此我们就已经将构造方法分析完毕,可以说就是最常见的数据结构中双向链表的操作方法。接下来我们继续分析一些常见的方法。
3、常用的方法
第一个add()
public boolean add(E e) {
linkLast(e);
return true;
}
/**
* Links e as last element.
*/
void linkLast(E e) {
final Node l = last;
final Node newNode = new Node<>(l, e, null);
last = newNode;
if (l == null)
first = newNode;
else
l.next = newNode;
size++;
modCount++;
}
我们来看看这个方法,首先定义了两个常量l和newNode结点。分别表示链表中最后一个结点和一个封装了新数据的新结点。新结点的前指针指向l。然后将last指针指向新结点。然后判断如果l结点(即之前的最后一个结点)是空,表明链表之前没有数据,加入的新数据将会称为第一个结点。
因此将表头first指针指向新结点。如果l不为空。则将之前最后一个结点的后指针指向新结点,新结点指向l。然后size自加1,modCount自加1表示修改了一次链表。这样就将新数据插入到了链表的末尾。
第二个add()方法:
首先是调用checkPositionIndex()方法检查index是否大于0并小于size。
然后如果index等于size,表示我们要将数据插入到链表的末尾,调用linkLast()方法来插入数据,上面分析了该方法这里就不在赘述。如果index不等于size,那么表示是在链表的中间插入数据,那么调用linkBefore()方法:
可以看到其实也是差不多的,首先定义两个常量Node变量pred和newNode用来表示我们要插入的结点的前结点和一个要插入的新结点,这个新结点的前指针指向pred,后指针指向插入位置的旧结点。然后将要插入位置的旧结点的prev前指针指向新结点。如果pred为空,表示我们要插入的位置是表头,直接将表头指针first指向新结点。如果不为空,那么将pred的后指针next指向新结点。
remove()方法
我们来看看第一个remove()方法,传入的参数表示是一个数据。虽然要首先判断我们传入的数据是否为空来分开操作。但是其实都是一样的做遍历然后删除结点。如果是空,那么就要进行for循环从表头开始遍历,有人可能会好奇,传入为空的话为什么还要找,没有意义呀?这里我的想法是链表是一种数据结构,它是以结点为基础存在的,不关心数据。所以有可能某个结点不为空,但是结点封装的数据为空。因此,在某些特殊场景下万一有些人就是要存空数据呢?我们重点看看unlink()方法:
首先将要删除结点的数据取出。然后得到删除结点的前结点prev,后结点next。然后如果前结点为空,表明删除结点为头结点,因此直接将表头first指针指向删除结点的后结点。否则的话将prev的next指针直接跳过删除结点指向next结点。然后将输出结点的prev指针置空。后面的next判空也是同理。最后将删除结点的数据置空,链表数量自减1,modCount自加1,然后删除结点的数据。至此,结点删除就已经完成。
接下来我们来看看第二个remove()方法:
这个更简单,移除指定的结点。还是首先检查index的合法性,然后得到指定位置的结点调用unlink()方法移除即可。上面已分析unlink()方法,就不再赘述。
第三个remove()方法:
说实话这个remove()方法我不是很理解为什么这些写,就是调用removeFirst()方法来移除表头结点。百思不得其解为什么要这么设计,而且remove()这个方法名也根本看不出是移除表头的意思。也没有什么可以分析的,就是一个简单的移除表头结点。
clear()方法
我们来看看clear()方法,顾名思义,clear就是将链表清空。所以直接一个for循环,从表头开始一直到表尾。将每个结点的数据直接置空即可。最后将表头,表尾first,last置空。size置为0即可。
get()方法
get()方法也很常用,我们来看看,首先调用checkElementIndex()方法检查index是否大于0并小于size。然后调用了node()方法来获取指定位置的结点。我们去看看:
我们看到,这里还是用了一点小技巧。首先判断我们想要的位置是否是在链表的前半部分还是后半部分(size >> 1 表示除以2),如果在前半部分那么就从表头开始遍历,在后半部分就从表尾开始往前遍历。知道拿到目标结点即可。
set()方法
首先也是调用checkElementIndex()方法检查index是否大于0并小于size。然后也是调用node()方法获取指定位置的结点。然后将指定结点的item数据置为新值,返回旧值即可。
至此我们常见的LinkedList的方法源码分析就已经完了,其他的一些方法要么不怎么用,要么非常简单只有一两行简单代码甚至就是调用这些常见方法,读者一跟进去就能明白,这里就不再深究。
二、总结
最后我们再来总结一下:
首先LinkedList内部是由双向链表来实现的。我们储存的每一个数据都会被封装在一个数据结点之中。而结点疯转了指向前结点的指针,数据,指向后结点的指针。依靠这些数据结点实现双向链表。
既然是链表,那么优点就是添加,插入,删除数据效率比数组高很多。因为在插入或者删除某个数据时,只需对要删除结点,前结点,后结点进行操作,无需像数组一样将后续数据全部前移或者后移。但是由此也看出缺点,因为链表并不是连续的空间储存,也没有什么下标进行记录位置。因此要寻找某个数据时只能进行遍历,而不像数组一样可以随机查找。如果我们在实际开发中我们需要对某个List进行频繁的插入,删除,而且数据量又特别大的时候。可以考虑使用LinkedList。