Scikit-Learn学习笔记——高斯混合模型(GMM)应用:分类、密度估计、生成模型
高斯混合模型
k-means聚类模型非常简单并且易于理解,但是他的简单性也为实际应用带来了挑战。特别是实际应用中,k-means的非概率性和它仅根据到簇中心点的距离来指派将导致性能低下。高斯混合模型可以看作是k-means的一个扩展,但它也是一种非常强大的聚类评估工具。
k-means算法的缺陷
在实际聚类的过程中,两个簇往往会存在重合部分。k-means算法对于重合部分的点被分配到哪个簇缺乏一个评估方案,k-means模型本身也没有度量簇的分配概率或不确定性的方法。
理解k-means模型的一个方法是,它在每个簇的中心放置了一个圆圈(在更高维空间是一个超空间),圆圈半径根据最远的点和簇中心点的距离算出。这个半径作为训练集分配的硬切断,即在这个圆圈之外的任何点都不是该簇的成员。而且,k-means要求这些簇的模型必须是圆形:k-means算法没有内置方法来实现椭圆形的簇。这就使得某些情况下k-means模型拟合出来的簇(圆形)与实际数据分布(可能是椭圆)差别很大,导致多个圆形的簇混在一起,相互重叠。
总的来说,k-means存在两个缺点——类的形状缺少灵活性、缺少簇分配的概率——使得它对许多数据集(特别是低维数据集)的拟合效果不尽如人意。
高斯混合模型
一个高斯混合模型试图找到多维高斯模型概率分布的混合体,从而找到任意数据最好的模型。在最简单的场景中,GMM可以用与k-means相同的方式寻找类。
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
#产生实验数据
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4,
cluster_std=0.60, random_state=0)
X = X[:, ::-1] #交换列是为了方便画图
from sklearn.mixture import GMM
gmm = GMM(n_components=4).fit(X)
labels = gmm.predict(X)
plt.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis');#由于GMM有一个隐含的概率模型,因此它也可能找到簇分配的概率结果——在Scikit-Learn中用predict_proba方法
#实现。这个方法返回一个大小为[n_samples, n_clusters]的矩阵,矩阵会给出任意属于某个簇的概率
probs = gmm.predict_proba(X)
print(probs[:5].round(3))
#输出结果
[[0.525 0.475 0. 0. ]
[0. 0. 0. 1. ]
[0. 0. 0. 1. ]
[1. 0. 0. 0. ]
[0. 0. 0. 1. ]]#将每个点簇分配的概率可视化
size = 50 * probs.max(1) ** 2 #平方放大概率的差异
plt.scatter(X[:, 0], X[:, 1], c=labels, cmap='viridis', s=size);最终结果表明,每个簇的结果并不与硬边缘的空间有关,而是通过高斯平滑模型实现。正如k-means中的期望最大化方法,这个算法又是并不是全局最优解,因此在实际应用中需要使用多个随机初始解。
使用GMM拟合拟合扁平椭圆的簇
from matplotlib.patches import Ellipse
def draw_ellipse(position, covariance, ax=None, **kwargs):
"""用给定的位置和协方差画一个椭圆"""
ax = ax or plt.gca()
#将协方差转换为主轴
if covariance.shape == (2, 2):
U, s, Vt = np.linalg.svd(covariance)
angle = np.degrees(np.arctan2(U[1, 0], U[0, 0]))
width, height = 2 * np.sqrt(s)
else:
angle = 0
width, height = 2 * np.sqrt(covariance)
#画出椭圆
for nsig in range(1, 4):
ax.add_patch(Ellipse(position, nsig * width, nsig * height,
angle, **kwargs))
def plot_gmm(gmm, X, label=True, ax=None):
ax = ax or plt.gca()
labels = gmm.fit(X).predict(X)
if label:
ax.scatter(X[:, 0], X[:, 1], c=labels, s=40, cmap='viridis', zorder=2)
else:
ax.scatter(X[:, 0], X[:, 1], s=40, zorder=2)
ax.axis('equal')
w_factor = 0.2 / gmm.weights_.max()
for pos, covar, w in zip(gmm.means_, gmm.covars_, gmm.weights_):
draw_ellipse(pos, covar, alpha=w * w_factor)#用椭圆形来拟合数据
rng = np.random.RandomState(13)
X_stretched = np.dot(X, rng.randn(2, 2))
gmm = GMM(n_components=4, covariance_type='full', random_state=42)
plot_gmm(gmm, X_stretched)GMM模型中的超参数convariance_type控制这每个簇的形状自由度。
- 它的默认设置是convariance_type=’diag’,意思是簇在每个维度的尺寸都可以单独设置,但椭圆边界的主轴要与坐标轴平行。
- covariance_type=’spherical’时模型通过约束簇的形状,让所有维度相等。这样得到的聚类结果和k-means聚类的特征是相似的,虽然两者并不完全相同。
- covariance_type=’full’时,该模型允许每个簇在任意方向上用椭圆建模。
将GMM用作密度估计
虽然GMM通常被归类为聚类算法,但他本质上是一个密度估计算法;也就是说,从技术的角度考虑,一个GMM拟合的结果并不是一个聚类模型,而是描述数据分布的生成概率模型。
#生成实验数据
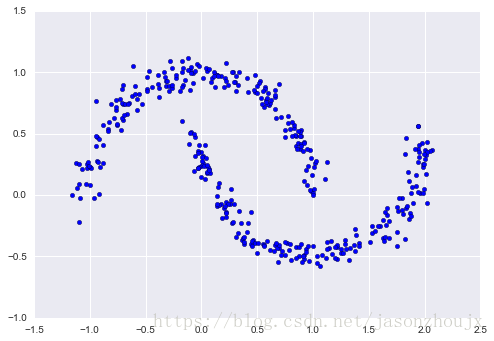
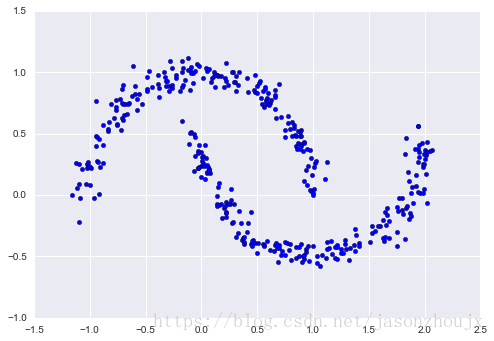
from sklearn.datasets import make_moons
Xmoon, ymoon = make_moons(200, noise=.05, random_state=0)
plt.scatter(Xmoon[:, 0], Xmoon[:, 1]);#如果用GMM对数据拟合出两个成分,那么作为一个聚类模型的结果,效果将会很差
gmm2 = GMM(n_components=2, covariance_type='full', random_state=0)
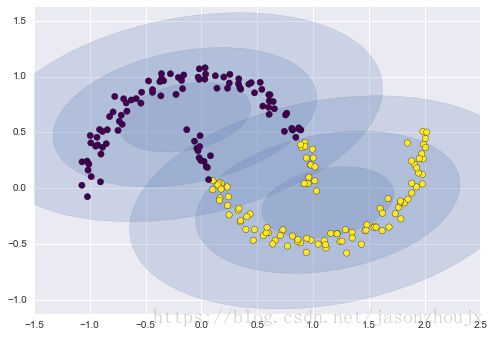
plot_gmm(gmm2, Xmoon)#如果选用更多的成分而忽视标签,就可以找到一个更接近输入数据的拟合结果
gmm16 = GMM(n_components=16, covariance_type='full', random_state=0)
plot_gmm(gmm16, Xmoon, label=False)这里采用16个高斯曲线的混合形式不是为了找到数据的分隔的簇,而是为了对输入数据的总体分布建模。通过拟合后的GMM模型可以生成新的、与输入数据类似的随即分布函数。GMM是一种非常方便的建模方法,可以为数据估计出任意维度的随即分布
Xnew = gmm16.sample(400, random_state=42)
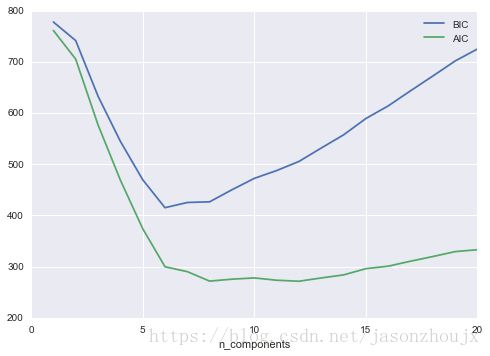
plt.scatter(Xnew[:, 0], Xnew[:, 1]);作为一种生成模型,GMM提供了一种确定数据集最优成分数量的方法。由于生成模型本身就是数据集的概率分布,因此可以利用模型来评估数据的似然估计,并利用交叉检验防止过拟合。Scikit-Learn的GMM评估器内置了两种纠正过拟合的标准分析方法:赤池信息量准则(AIC)和贝叶斯信息准则(BIC)
n_components = np.arange(1, 21)
models = [GMM(n, covariance_type='full', random_state=0).fit(Xmoon)
for n in n_components]
plt.plot(n_components, [m.bic(Xmoon) for m in models], label='BIC')
plt.plot(n_components, [m.aic(Xmoon) for m in models], label='AIC')
plt.legend(loc='best')
plt.xlabel('n_components');示例:用GMM生成新的数据
前面介绍了一个将GMM作为数据生成器模型的示例,目的是根据输入数据的分布创建一个新的样本集。现在利用这个思路,为标准手写数字库生成新的手写数字
#导入手写数字数据
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shape
#画出前100个数据
def plot_digits(data):
fig, ax = plt.subplots(10, 10, figsize=(8, 8),
subplot_kw=dict(xticks=[], yticks=[]))
fig.subplots_adjust(hspace=0.05, wspace=0.05)
for i, axi in enumerate(ax.flat):
im = axi.imshow(data[i].reshape(8, 8), cmap='binary')
im.set_clim(0, 16)
plot_digits(digits.data)#使用PCA进行降维,让PCA算法保留投影后样本99%的方差
from sklearn.decomposition import PCA
pca = PCA(0.99, whiten=True)
data = pca.fit_transform(digits.data)
#对这个降维的数据使用AIC,从而得到GMM成分数量的粗略估计
n_components = np.arange(50, 210, 10)
models = [GMM(n, covariance_type='full', random_state=0)
for n in n_components]
aics = [model.fit(data).aic(data) for model in models]
plt.plot(n_components, aics);#在大约110个成分的时候,AIC是最小的,因此我们打算使用这个模型生成新的数据
#确认模型已经收敛
gmm = GMM(110, covariance_type='full', random_state=0)
gmm.fit(data)
print(gmm.converged_)
#输出结果:
True#使用GMM模型在降维的空间中画出100个新的手写数字样本,再使用PCA对象逆变换将其恢复到原始的空间
data_new = gmm.sample(100, random_state=0)
digits_new = pca.inverse_transform(data_new)
plot_digits(digits_new)