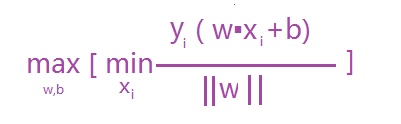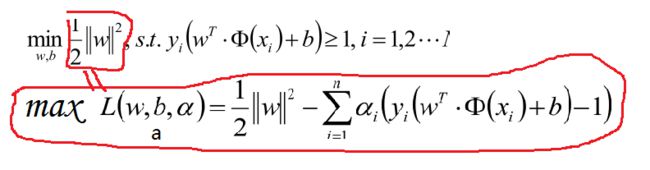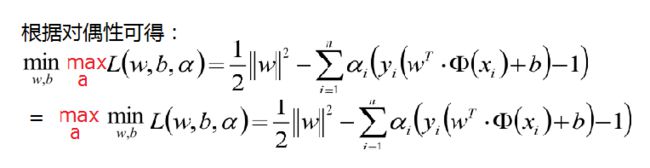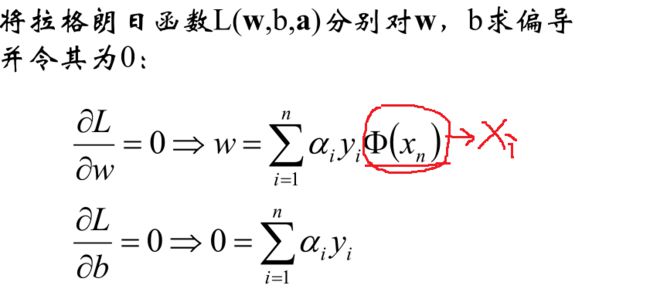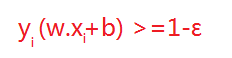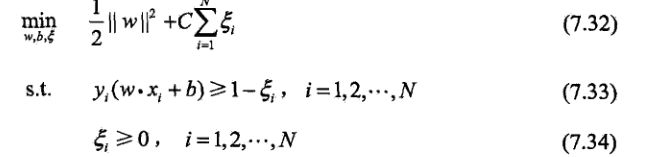svm算法 最通俗易懂讲解

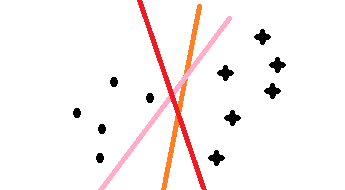
  最近在学习svm算法，借此文章记录自己的学习过程，在学习很多处借鉴了z老师的讲义和李航的统计，若有不足的地方，请海涵；svm算法通俗的理解在二维上，就是找一分割线把两类分开，问题是如下图三条颜色都可以把点和星划开，但哪条线是最优的呢，这就是我们要考虑的问题；

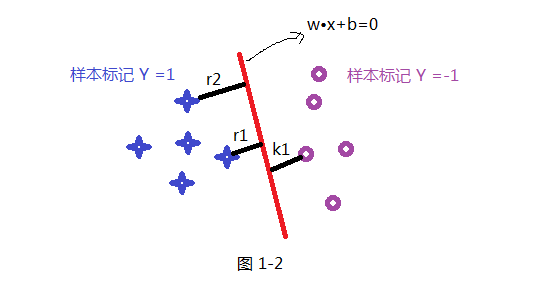
首先我们先假设一条直线为 W•X+b =0 为最优的分割线，把两类分开如下图所示，那我们就要解决的是怎么获取这条最优直线呢?及W 和 b 的值；在SVM中最优分割面(超平面)就是：能使支持向量和超平面最小距离的最大值；

我们的目标是寻找一个超平面，使得离超平面比较近的点能有更大的间距。也就是我们不考虑所有的点都必须远离超平面，我们关心求得的超平面能够让所有点中离它最近的点具有最大间距。

如上面假设蓝色的星星类有5个样本，并设定此类样本标记为Y =1，紫色圈类有5个样本，并设定此类标记为 Y =-1，共 T ={(X₁ ,Y₁) , (X₂,Y₂) (X₃,Y₃) .........} 10个样本，超平面（分割线）为wx+b=0;  样本点到超平面的几何距离为：

    

        此处要说明一下：函数距离和几何距离的关系；定义上把 样本| w▪x₁+b|的距离叫做函数距离，而上面公式为几何距离，你会发现当w 和b 同倍数增加时候，函数距离也会通倍数增加；简单个例子就是，样本 X₁ 到 2wX₁+2b =0的函数距离是wX₁ +b =0的函数距离的 2倍；而几何矩阵不变；

        下面我们就要谈谈怎么获取超平面了？！

超平面就是满足支持向量到其最小距离最大，及是求：max [支持向量到超平面的最小距离] ；那只要算出支持向量到超平面的距离就可以了吧 ，而支持向量到超平面的最小距离可以表示如下公式:

故最终优化的的公式为：

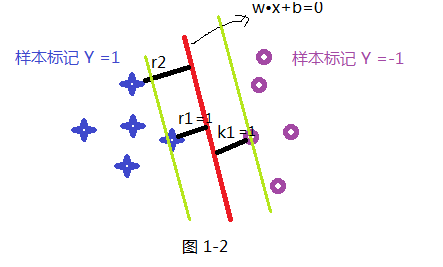
 根据函数距离和几何距离可以得知，w和b增加时候，几何距离不变，故怎能通过同倍数增加w和 b使的支持向量（距离超平面最近的样本点）上样本代入 y(w*x+b) =1,而不影响上面公式的优化，样本点距离如下：如上图其r1函数距离为1，k1函数距离为1,而其它

样本点的函数距离大于1，及是：y(w•x+b)>=1，把此条件代入上面优化公式候，可以获取新的优化公式1-3：

公式1-3见下方：优化最大化分数，转化为优化最小化分母，为了优化方便转化为公式1-4

为了优化上面公式，使用拉格朗日公式和KTT条件优化公式转化为：

对于上面的优化公式在此说明一下：比如我们的目标问题是 minf(x)。可以构造函数L(a,b,x)：

L(a,b,x)=f(x)+a⋅g(x)+b⋅h(x)，a≥0

此时 f(x) 与 maxa,bL(a,b,x) 是等价的。因为 h(x)=0,g(x)≤0,a⋅g(x)≤0，所以只有在a⋅g(x)=0 的情况下

L(a,b,x) 才能取得最大值，因此我们的目标函数可以写为minxmaxa,bL(a,b,x)。如果用对偶表达式：maxa,bminxL(a,b,x)，

由于我们的优化是满足强对偶的（强对偶就是说对偶式子的最优值是等于原问题的最优值的），所以在取得最优值x∗ 的条件下，它满足 :

f(x∗)=maxa,bminxL(a,b,x)=minxmaxa,bL(a,b,x)=f(x∗)，

结合上面的一度的对偶说明故我们的优化函数如下面，其中a >0

现在的优化方案到上面了，先求最小值，对 w 和 b 分别求偏导可以获取如下公式：

把上式获取的参数代入公式优化max值：

化解到最后一步，就可以获取最优的a值：

以上就可以获取超平面！

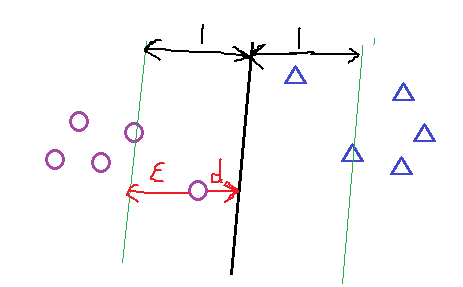
但在正常情况下可能存在一些特异点，将这些特异点去掉后，剩下的大部分点都能线性可分的，有些点线性不可以分，意味着此点的函数距离不是大于等于1，而是小于1的，为了解决这个问题，我们引进了松弛变量 ε>=0; 这样约束条件就会变成为：

故原先的优化函数变为：

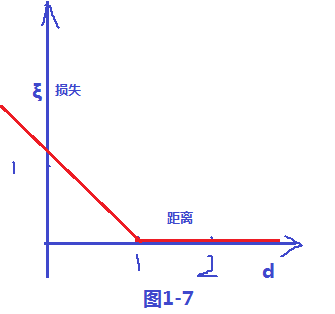
对加入松弛变量后有几点说明如下图所以；距离小于1的样本点离超平面的距离为d ,在绿线和超平面之间的样本点都是由损失的，

其损失变量和距离d 的关系，可以看出 ξ = 1-d , 当d >1的时候会发现ξ =0，当 d<1 的时候 ξ = 1-d ;故可以画出损失函数图，如下图1-7；样式就像翻书一样，我们把这个损失函数叫做 hinge损失；

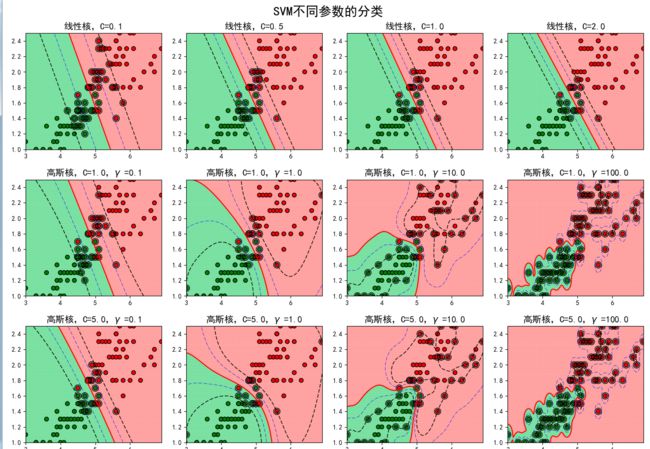
下面我们简单的就来讨论一下核函数：核函数的作用其实很简单就是把低维映射到高维中，便于分类。核函数有高斯核等,下面就直接上图看参数对模型的影响，从下图可以了解，当C变化时候，容错变小，泛化能力变小；当选择高斯核函数的时候，随时R参数调大，准确高提高，最终有过拟合风险；

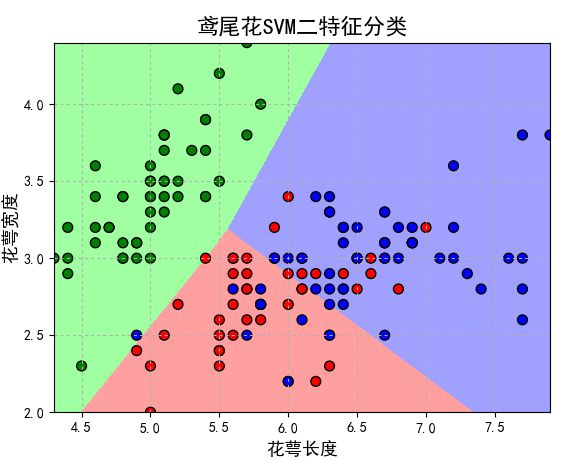
下面就直接上代码了（鸢尾花SVM二特征分类）：

iris_feature = u'花萼长度', u'花萼宽度', u'花瓣长度', u'花瓣宽度'


if __name__ == "__main__":
    path = 'iris.data'  # 数据文件路径
    data = pd.read_csv(path, header=None)
    x, y = data[range(4)], data[4]
    y = pd.Categorical(y).codes
    x = x[[0, 1]]
    x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1, train_size=0.6)

    # 分类器
    clf = svm.SVC(C=0.3, kernel='linear', decision_function_shape='ovo')
    clf.fit(x_train, y_train.ravel())

    # 准确率
    print clf.score(x_train, y_train)  # 精度
    print '训练集准确率：', accuracy_score(y_train, clf.predict(x_train))
    print clf.score(x_test, y_test)
    print '测试集准确率：', accuracy_score(y_test, clf.predict(x_test))
    x1_min, x2_min = x.min()
    x1_max, x2_max = x.max()
    x1, x2 = np.mgrid[x1_min:x1_max:500j, x2_min:x2_max:500j]  # 生成网格采样点
    grid_test = np.stack((x1.flat, x2.flat), axis=1)  # 测试点

    print 'grid_test = \n', grid_test
    Z = clf.decision_function(grid_test)
    Z = Z[:,0].reshape(x1.shape)
    print "decision_function:",Z
    grid_hat = clf.predict(grid_test)
    grid_hat = grid_hat.reshape(x1.shape)
    mpl.rcParams['font.sans-serif'] = [u'SimHei']
    mpl.rcParams['axes.unicode_minus'] = False

    cm_light = mpl.colors.ListedColormap(['#A0FFA0', '#FFA0A0', '#A0A0FF'])
    cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
    plt.figure(facecolor='w')
    plt.pcolormesh(x1, x2, grid_hat, cmap=cm_light)
    plt.scatter(x[0], x[1], c=y, edgecolors='k', s=50, cmap=cm_dark)      # 样本
    plt.scatter(x_test[0], x_test[1], s=120, facecolors='none', zorder=10)     # 圈中测试集样本
    plt.xlabel(iris_feature[0], fontsize=13)
    plt.ylabel(iris_feature[1], fontsize=13)
    plt.xlim(x1_min, x1_max)
    plt.ylim(x2_min, x2_max)
    plt.title(u'鸢尾花SVM二特征分类', fontsize=16)
    plt.grid(b=True, ls=':')
    plt.show()

最后画图如下：