动态规划之背包问题,简洁版本C++代码及分析
小议动态规划之背包问题
- 1、01背包问题
- 2、完全背包问题
蒟蒻一枚,本来想把学算法的心得写在笔记本上,想到可以来社区写写博客,和网友们交流心得,第一次写有不好的地方欢迎指正,后续会慢慢改进。
下面进入正题,我们先讨论几种基础的背包问题,01背包、完全背包、多重背包、多重背包的二进制优化、分组背包。内容参阅了DD大牛的《背包九讲》,以及ACwing社区,可以系统学算法以及刷题,良心推荐大家有空可以去瞧瞧。
1、01背包问题
有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。第 i 件物品的体积是 vi,价值是 wi。求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。
输入格式:
第一行两个整数,N,V,用空格隔开,分别表示物品数量和背包容积。
接下来有 N 行,每行两个整数 vi,wi,用空格隔开,分别表示第 i 件物品的体积和价值。
输出格式:
输出一个整数,表示最大价值。
数据范围
0
4 5
1 2
2 4
3 4
4 5
输出样例:
8

考虑动态规划问题我们可以分为两步,一是状态表示,二是状态计算。状态表示一般就是一个一维或者多维数组,每维的参数表示不同的意义,整个数组一般表示 最大值、最小值、最优解等我们要求的东西,状态计算则是我们要自己推导的递推表达式。
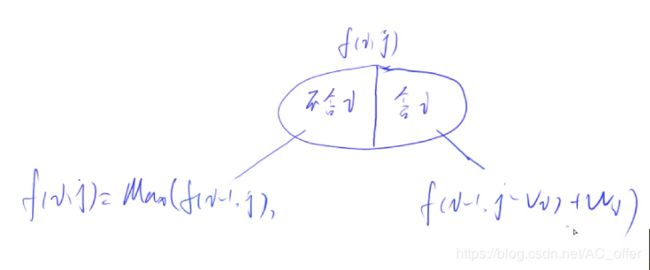
初始我们用二维数组表示,i 表示目前选到第几个,j 表示目前背包的容量,f[i][j]表示选完之后价值最大。代码如下
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m, v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
{
f[i][j] = f[i-1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i-1][j - v[i]] + w[i]);
}
cout << f[n][m];
return 0;
}
时间和空间复杂度均为O(N*V),其中时间复杂度基本已经不能再优化了,但空间复杂度却可以优化到O(V)。即用一维数组来表示。
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m, v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = m; j >= v[i]; j--)
{
// f[i][j] = f[i-1][j];
f[j] = max(f[j], f[j - v[i]] + w[i]);
}
cout << f[m];
return 0;
}
- 上面的基本思路如何实现? 有一个主循环 i=1…N,每次算出来二维数组 f[i][0…V] 的所有值。那么,如果只用一个数组 f [0…V],能不能保证第i次循环结束后 f[v] 中表示的就是我们定义的状态f[i][v]呢?
- f[i][v] 是由 f[i-1][v] 和 f[i-1] [v-c[i]] 两个子问题递推而来,能否保证在推 f[i][v] 时(也即在第i次主循环中推 f[v] 时)能够得到 f[i-1][v] 和 f[i-1][v -c[i]] 的值呢?事实上,这要求在每次主循环中我们以v=V…0的顺序推 f[v],这样才能保证推 f[v] 时 f[v-c[i]] 保存的是状态 f[i -1][v-c[i]] 的值。
2、完全背包问题
题目描述和输入输出与01问题一致,但是每种物品都有无限件可用。
输入样例
4 5
1 2
2 4
3 4
4 5
输出样例:
10
解题思路和上面的一致,每种物品有无限件。也就是从每种物品的角度考虑,与它相关的策略已并非取或不取两种,而是有取0件、取1件、取2件……等很多种。如果仍然按照解01背包时的思路,令f[i][v]表示前i种物品恰放入一个容量为v的背包的最大权值。仍然可以按照每种物品不同的策略写出状态转移方程,像这样:f[i][v]=max{f[i-1][v-kc[i]]+kw[i]|0<=kc[i]<= v}。这跟01背包问题一样有O(NV)个状态需要求解,但求解每个状态的时间则不是常数了,求解状态f[i][v]的时间是O(v/c[i]),总的复杂度是超过O(VN)的。
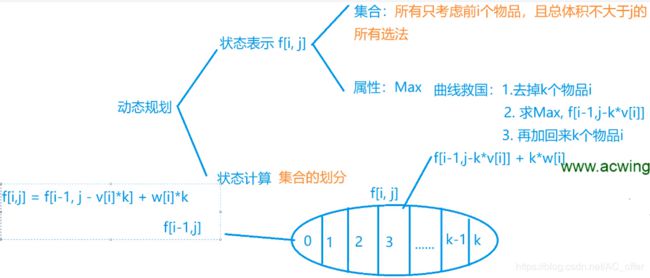
暴力代码如下,复杂度是超过O(VN)
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m, v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
for(int k = 0; k <= j/v[i]; k++)
{
f[i][j] = max(f[i][j], f[i-1][j - k*v[i]] + k*w[i]);
}
cout << f[n][m];
return 0;
}
01背包是从第 i - 1层转移过来的,而完全背包是从第 i 层转移的,这是两者的不同之处,也是优化问题的重点所在。

初步优化,复杂度是O(VN)
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m, v[N], w[N];
int f[N][N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = 0; j <= m; j++)
//for(int k = 0; k <= j/v[i]; k++)
{
f[i][j] = f[i-1][j];
if(j >= v[i]) f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);
}
cout << f[n][m];
return 0;
}
空间优化成一维
#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1010;
int n, m, v[N], w[N];
int f[N];
int main()
{
cin >> n >> m;
for(int i = 1; i <= n; i++)
cin >> v[i] >> w[i];
for(int i = 1; i <= n; i++)
for(int j = v[i]; j <= m; j++)
{
//f[i][j] = f[i-1][j];
f[j] = max(f[j], f[j - v[i]] + w[i]); //从第i层转移过来的
}
cout << f[m];
return 0;
}
先想想为什么01中要按照 v=V…0 的逆序来循环。这是因为要保证第i次循环中的状态 f[i][v] 是由状态 f[i-1][v-c[i]] 递推而来。换句话说,这正是为了保证每件物品只选一次,保证在考虑“选入第i件物品”这件策略时,依据的是一个绝无已经选入第i件物品的子结果 f[i-1][v-c[i]] 。而现在完全背包的特点恰是每种物品可选无限件,所以在考虑“加选一件第i种物品”这种策略时,却正需要一个可能已选入第i种物品的子结果 f[i][v-c[i]],所以就可以并且必须采用v= 0…V的顺序循环。这就是这个简单的程序为何成立的道理。 (背包九讲)
先写到这儿,累,花了我一个上午,后续的多重背包以及其二进制优化,分组背包等问题等后续更新,有其他的想法可以私聊,对每一道动态规划题目都思考其方程的意义以及如何得来,是加深对动态规划的理解、提高动态规划功力的好方法。 以上解题思路的图片来源于ACwing yxc奆佬的授课视频截图,已获其同意,仅用于算法爱好者分享,求互粉及交流谢谢大家。