信奥学习阶段性总结(理解依旧不深)//2018/7/20
写在前面：垃圾蒟蒻的又一篇水文欢迎在评论区指出错误，吐槽，灌水，喷。(想要个评论怎么这么难)
目录
引
第一章：LCA
dfs建树
求LCA
时间复杂度证明
第二章：树上差分
树上差分前缀和的计算
树状数组
第四章：概率与期望dp
完
引
愉快(poi)的学习又告一段落，又学了不少东西，又需要进行备份了(这次不是老师让咱写的哟)，不能变白色了，差评。
这段时间，本蒟蒻总共学了如下几个东西：
- 莫队(get a little) 传送门
- LCA(get !)
- 树上差分(get !)
- 树状数组(already get it)
- 树上dp(get a little)
- 搜索(already get)
- KMP算法，字典树 ，MANACHER(trie to get again)
- 概率与期望dp(not get)
- 数论(？)(can not get )
- 斜率优化，四边形不等式(I just can not get what my teacher said!!!)
- 线段树(I don't down if I have already get it or not)
有没有发现，其实好多都学过了，但要填的坑也蛮多的
下面是几个等级：完全不懂，懂了一点，基本掌握，学会了一点点运用，不知道算不算懂
第一章：LCA
LCA(Least Common Ancestors),中文意思是最近公共祖先，如图
，注意，一定是最近公共祖先，在途中的4,5两个点的LCA是2，因为点3不是点5的祖先，而点1虽然是两个点的共同祖先，但他的有点2离4,5,两个点近，即不是最近。所以点2是4,5两个点的LCA，对于树上的两个点，他们的LCA有且只有一个(当一个点就是另一个点的祖先的时候，他就是两个点的LCA)。
LCA的用处貌似还挺多的，换句话说贼好用。
好了，说了那么多，来讲讲怎么求LCA吧
其实求LCA的方法有很多种，其中本蒟蒻目前只听到了三种：离线求LCA(tarjan(又是他)+并查集)，倍增求LCA，RMQ求LCA(当然还有可爱的暴力求LCA啦)，其中，本蒟蒻最喜欢倍增求LCA，所以就来讲讲怎么做到这一点吧。
首先要引入几个概念
- 链式前向星：相信都会，只不过这东东的叫法比较多：邻接表，边链表等等都是他的别名
- 点的深度：相信大家也都听说过，一个点的深度就是他到根节点所经过的变得条数，根节点的深度为0
- 倍增：一种思想，应该算比较常见了，主要是通过二进制一n个二的ki次方{ki
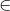Z}，将任意一个数表达出来，方便计算
也就这么三个简单的概念
以下是代码实现，分为两个部分：dfs建树与logn求LCA
dfs建树
void int dfs(int x,int fatehr)
{
deep[x]=deep[father]+1;
subtree[x][0]=father;
for(int i=1;(1<
其中由于树的性质：一个点的父亲节点的深度肯定比儿子节点小，所以第二个for循环内的特判可以帮助我们一直向下搜索而不用担心又往回搜到根节点
而第一个循环内的则表示这一个点每次倍增跳到的节点；
求LCA
int LCA(int x,int y)
{
if(x==y) return x;
if(deep[x]=0;--i)
if(deep[x]-(1<=deep[y])
x=subtree[x][i];
if(x==y) retrun x;
for(int i=block;i>=0;--i)
if(subtree[x][i]!=subtree[y][i])
x=subtree[x][i],y=[y][i];
retrun subtree[x][0];
}
请允许本蒟蒻解释一下这个代码
- block是一个int形变量，记录了最深的点倍增一共跳了几次：求法
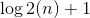
- 本段代码中的前两句话是为了确保x的深度比y深，为了使第一个for循环可以把x,y的深度拉至同一深度。
- 第二个for循环则是使两个点同时往上跳，直到跳不动了(两个点重合)，就找到了LCA
时间复杂度证明
只能简单的证明一下了，由于倍增的方法是每次把当前的数乘上2，所以一个数最多要跳
次，所以时间复杂度就是
啦。
第二章：树上差分
想学习这章的同学请先学习LCA与差分
树上差分，听名字就知道与树和差分脱不了干系，没错，树上差分就是差分思想在树上实现的结果
那么为什么要先学习LCA呢？因为树上差分的差分过程需要用到LCA，
树上差分一共有点差分与边差分两种，今天我们主要讲的是点差分
点差分的基本思路几乎和数组上的差分一模一样
唯一一点不同的就是差分点的选择与前缀和的求法不同而已，貌似找不到图片了，又不想自己做桑心
那么就来草率的理解一下吧，假设我们，要把4,5两个点+1,很明显的，我们首先要把4,5两个点的差分数组++，然后我们来考虑要把那些点-1；
（还是刚刚的图）
第一，我们要明确这个前缀和数组是怎么求的：这个前缀和数组是从根节点出发，一次向下遍历(有点像dfs建树)，然后再把后面的值累加到前缀和上的。那么，我们就可以得知，从叶子节点4,5回溯回根节点的时候，他们的LCA被累加了两次，所以LCA要-1，然后应为对于LCA上面的点，他们的值并没有发生改变，所以他们本来因该-2，但是由于LCA已经-1了，所以只要再把LCA的father节点-1就可以了。
树上差分前缀和的计算
具体方法上文已经讲述了，相信各位大佬看到代码就会明白的
void findf(int x)
{
for(int i=linkk[x];i;i=e[i].to)
{
if(e[i].to==subtree[x][0])
continue;
dfs(e[i].to);
cf[x]+=cf[e[i].to];
}
}
树状数组
树状数组是好久事前的事了，一维树状数组的请参见本蒟蒻的另一篇博文 传送门
这里就来讲一下二维的树状数组
二维的树状数组其实和一维的一样，只不过多了一重循环罢了，所以不再描述
第四章：概率与期望dp
怎么就到最后一章了？？？因为其他东西在另一篇blog中已经讲过了好吗，连接就在树状数组的传送门上
童鞋，知道概率与期望dp的模板题吗？？ 概率充电器传送门 题解传送门
同样，也先明确几个概念
- dp：…………
- 概率：大家应该都知道吧…………
- 期望：一件事情发生的概率乘上他发生所产生的影响(诸如价值之类的)叫它的期望。
概率与期望dp很好的把概率，期望，dp三者联系在了一起，贼有用，也贼好想状态，但是贼难转移(像我这种蒟蒻，看到满屏的式子就难受，嘎~~~,浑身难受）
简单的来说，概率与期望dp就是从一件事情的概率通过dp的方式推出另一件事情的概率，也正是由于这个性质，这类问题需要具体问题具体分析，不存在板子之类的，也就理所当然的没有代码啦
完
看什么呢，本文没有彩蛋
蒟蒻原创，转载请注明出处(虽然依然觉得没有人会转载)