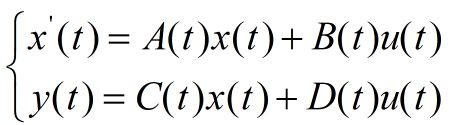MATLAB仿真PID控制器与模糊控制器
摘要：使用matlab编写PID控制器与模糊控制器，并对原理进行解析。
背景： 小白自学。
基础：1、视频“自动控制原理”，1-3章，柠檬大学，点此链接
2、《基于MATLAB的系统分析与设计——模糊系统》，楼顺天等，西安电子科技大学出版社，1-80页。
3、视频“单片机STM32——PID算法讲解”，1-6节，ArgonGhost，哔哩哔哩，点此链接。
4、视频“第9章线性系统的状态空间分析与综合（1）”，第一节，张超，哔哩哔哩，点此链接。
目录
一、控制案例
二、重要概念说明
2.1 PID控制原理
2.1.1 位置式PID
2.1.2 增量式PID
2.2 状态空间标准式
2.3 龙格-库塔法
一、控制案例
在此通过一个典型案例编写PID控制器和模糊控制器代码，并进行注释。（例子为《基于MATLAB的系统分析与设计——模糊系统》例3.8）
例：典型二阶系统的模糊控制与 传统PID控制的性能比较。通常的工业过程可以等效成二阶系统加上一些典型的非线性环境，如死区、饱和、纯延迟等，这里假设系统为
（1）
控制执行结构具有0.07的死区和0.7的饱和区，取样时间间隔T=0.01。
解：在PID仿真中，经过仔细选择，取
，
，
。在模糊控制仿真中，
，
，
，
，模糊控制器输出为
（2）
其中积分项用于消除控制系统的稳态误差。
MATLAB程序中，Nd用于表示系统的纯延迟（
），umin用于表示控制的死区电平，umax用于表示饱和电平。当Nd=0时，表示系统不存在纯延迟。MATLAB程序如下：
% -----------------------------------------
% 典型二阶系统的模糊控制与传统PID控制的性能比较
% -----------------------------------------
num=20;
den=[1.6,4.4,1];
[a1,b,c,d]=tf2ss(num,den); %将传递函数转换为状态空间，[1]
x=[0;0]; %有两个输入所以状态向量为二维
T=0.01;h=T;
umin=0.07;umax=0.7; %死区和饱和区
td=0.02;Nd=td/T;
N=500;R=1.5*ones(1,N); %稳态为1.5，存入R一维矩阵
% -------------
% PID 控制
% -------------
e=0;de=0;ie=0; %初始误差、误差微分、误差积分
kp=5;ki=0.1;kd=0.001; %PID控制器的三个参数
for k=1:N %重复1~500
uu1(1,k)=-(kp*e+ki*de+kd*ie); %计算本次PID控制器的输出
if k<=Nd %延迟调整
u=0;
else
u=uu1(1,k-Nd);
end
if abs(u) <= umin %死区和饱和区调整
u=0;
elseif abs(u) > umax
u=sign(u) * umax;
end
k0=a1*x+b*u; %利用龙格-库塔法进行系统仿真，[2]
k1=a1*(x+h*k0/2)+b*u;
k2=a1*(x+h*k1/2)+b*u;
k3=a1*(x+h*k2)+b*u;
x=x+(k0+2*k1+2*k2+k3)*h/6;
y=c*x+d*u;
e1=e; %计算误差、微分和积分
e=y(1,1)-R(1,k);
de=(e-e1)/T;
ie=e*T+ie;
yy1(1,k)=y; %将本次系统输出存入yy1矩阵
end
% -------------
% 模糊控制
% -------------
a=newfis('Simple');
a=addvar(a,'input','e',[-6 6]); %添加误差输入变量
a=addmf(a,'input',1,'NB','trapmf',[-6,-6,-5,-3]); %添加误差隶属函数
a=addmf(a,'input',1,'NS','trapmf',[-5,-3,-2 0]);
a=addmf(a,'input',1,'ZR','trimf',[-2,0,2]);
a=addmf(a,'input',1,'PS','trapmf',[0,2,3,5]);
a=addmf(a,'input',1,'PB','trapmf',[3,5,6,6]);
a=addvar(a,'input','de',[-6 6]); %添加误差变化输入变量
a=addmf(a,'input',2,'NB','trapmf',[-6,-6,-5,-3]); %添加误差变化隶属函数
a=addmf(a,'input',2,'NS','trapmf',[-5,-3,-2,0]);
a=addmf(a,'input',2,'ZR','trimf',[-2,0,2]);
a=addmf(a,'input',2,'PS','trapmf',[0,2,3,5]);
a=addmf(a,'input',2,'PB','trapmf',[3,5,6,6]);
a=addvar(a,'output','u',[-3 3]); %添加输出变量
a=addmf(a,'output',1,'NB','trapmf',[-3,-3,-2,-1]); %添加输出隶属函数
a=addmf(a,'output',1,'NS','trimf',[-2,-1,0]);
a=addmf(a,'output',1,'ZR','trimf',[-1,0,1]);
a=addmf(a,'output',1,'PS','trimf',[0,1,2]);
a=addmf(a,'output',1,'PB','trapmf',[1,2,3,3]);
rr =[5 5 4 4 3 %以下为计算模糊规则
5 4 4 3 3
4 4 3 3 2
4 3 3 2 2
3 3 2 2 1];
r1=zeros(prod(size(rr)),3);k=1;
for i=1:size(rr,1)
for j=1:size(rr,2)
r1(k,:)=[i,j,rr(i,j)];
k=k+1;
end
end
[r,s]=size(r1);
r2=ones(r,2);
rulelist=[r1,r2]; %计算模糊规则结束
a=addrule(a,rulelist); %添加模糊规则到模糊控制器
e=0;de=0;ie=0; %初始化误差、误差微分、误差积分
x=[0;0]; %初始化状态向量
ke=60;kd=2.5;ki=0.01;ku=0.8; %模糊控制器参数
for k=1:N %1~500
e1=ke*e; %输入变量变换至论域
de1=kd*de;
if e1>=6 %误差边界调整
e1=6;
elseif e1<=-6
e1=-6;
end
if de1>=6 %误差微分边界调整
de1=6;
elseif de1<=-6
de1=-6;
end
in=[e1 de1]; %输入向量
uu(1,k)=ku*evalfis(in,a)-ki*ie; %根据式2计算模糊控制器输出
if k<=Nd %延迟调整
u=0;
else
u=uu(1,k-Nd);
end
if abs(u)<=umin %死区、饱和区调整
u=0;
elseif abs(u)>umax
u=sign(u)*umax;
end
k0=a1*x+b*u; %利用龙格-库塔法进行系统仿真
k1=a1*(x+h*k0/2)+b*u;
k2=a1*(x+h*k1/2)+b*u;
k3=a1*(x+h*k2)+b*u;
x=x+(k0+2*k1+2*k2+k3)*h/6;
y=c*x+d*u;
e1=e; %计算误差、微分和积分
e=y-R(1,k);
de=(e-e1)/T;
ie=ie+e*T;
yy(1,k)=y; %将本次系统输出存入yy矩阵
end
% -------------
% 画图比较
% -------------
kk=[1:N]*T;
figure(1);
plot(kk,R,'k',kk,yy1,'b',kk,yy,'r'); %将PID控制和模糊控制同时显示
xlabel('时间（0.01秒）');
ylabel('输出');
gtext('模糊控制');gtext('PID控制');
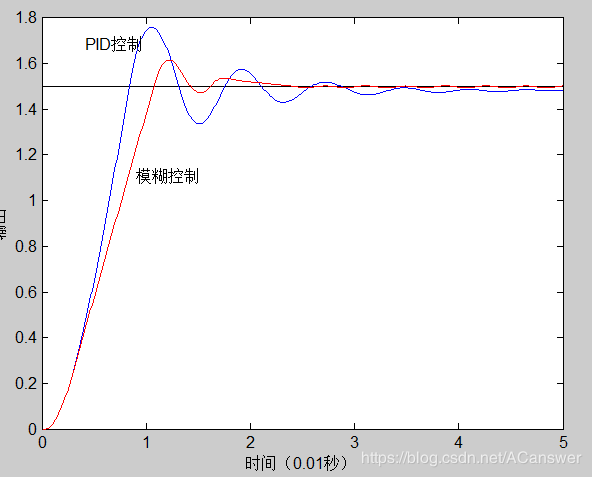
运行，输出如下：
二、重要概念说明
2.1 PID控制原理
PID控制分为位置式控制和增量式控制，大多数情况下为位置式PID控制。
2.1.1 位置式PID
基本公式： （3）
即： （4）
其中 
（5）
（6）
其中：
为比例系数，
为k时刻的误差，
为采样周期（计算周期，控制周期），
为积分常数（积分时间），
为微分常数
采样周期：单片机不能不停计算输出，因为可能上一次的计算输出还没有加到控制对象上，需要根据实际系统延迟。
积分常数：
和
共同作用的时间，越大，减弱输出信号；越小，增加输出信号；相当于历史误差的惩罚权值，人为给定。
例，早上第一次温度调控，室温为20度，目标为100度，当从20度第一次到100度时，由于达到目标值输出为0，但积分项考虑历史数据累积了大量误差，所以仍然会有输出，产生超调。有些算法为了避免超调，在第一次到达目标值时将积分常数选得非常大，减弱积分项的作用，这种方法为积分分离。积分项用于在比例项达标时控制（此时比例项无输出），即在到达目标之后才能体现积分项的作用。
微分常数：和
共同作用的时间，采样周期越大，相同误差下误差变化率越小（影响）。相当于误差变化的惩罚权值，人为给定。
2.1.2 增量式PID
位置式PID的输出量为直接控制量； 增量式PID的输出为控制变化量，即实际输出为当前控制量加上控制变化量，公式如下：
2.2 状态空间标准式
在说明状态空间标准式之前，说明下本例子总体控制模型，如下：
线性系统状态空间描述：
输入向量：![u=[u_{1},u_{2},...,u_{p}]^{T}](http://img.e-com-net.com/image/info8/34560ec5970941c580d9bcf5a6370395.gif){kind=small}
输出向量：![y=[y_{1},y_{2},...,y_{q}]^{T}](http://img.e-com-net.com/image/info8/ecc39607ff64464faa2f7ff429910400.gif){kind=small}
系统内部状态向量：![x=[x_{1},x_{2},...,x_{n}]^{T}](http://img.e-com-net.com/image/info8/9340dd1a80f04ae585248d1a7127c987.gif){kind=small}
，中间某一时刻的状态。
状态空间标准式：
（7）
其中，x为n维向量，u为p维向量，y为q维向量，A为nxn矩阵，B为nxq矩阵，C为qxn矩阵，D为qxp矩阵。
本文重点！：在此案例中u(t)为PID控制器或模糊控制器输出量。整体过程为：首先根据当前误差和误差变化输入到PID控制器或模糊控制器，输出为u(t)，然后根据龙格-库塔法对状态空间标准式（即7式）求出输出y。
2.3 龙格-库塔法
该方法不用求解微分方程直接计算下一个点的值，以下摘百度百科。
在各种龙格－库塔法当中有一个方法十分常用，以至于经常被称为“RK4”或者就是“龙格－库塔法”。该方法主要是在已知方程导数和初值信息，利用计算机仿真时应用，省去求解微分方程的复杂过程。
令初值问题表述如下。
则，对于该问题的RK4由如下方程给出：
这样，下一个值（yn+1）由现在的值（yn）加上时间间隔（h）和一个估算的斜率的乘积所决定。该斜率是以下斜率的加权平均：
-
k1是时间段开始时的斜率；
-
k2是时间段中点的斜率，通过欧拉法采用斜率k1来决定y在点tn+h/2的值；
-
k3也是中点的斜率，但是这次采用斜率k2决定y值；
-
k4是时间段终点的斜率，其y值用k3决定。
当四个斜率取平均时，中点的斜率有更大的权值：
RK4法是四阶方法，也就是说每步的误差是h阶，而总积累误差为h阶。
注意上述公式对于标量或者向量函数（y可以是向量）都适用。