求最大公约数

一、题目分析

①　随机产生20组随机数
②　分别用辗转相除法、穷举法、更相减损法和Stein算法求最大公约数。
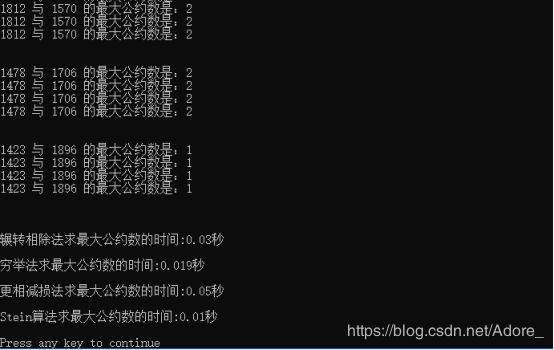
③　求出各个算法求取最大公约数的时间
④　比较算法优劣性

二、算法设计

①　辗转相除法
1.先用小的一个数除大的一个数，得第一个余数
2.再用第一个余数除小的一个数，得第二个余数
3.又用第二个余数除第一个余数，得第三个余数
4.逐次用后一个数去除前一个余数，直到余数是0为止。那么，最后一个除数就是所求的最大公约数

②　穷举法
对两个正整数a,b如果能在区间[a,0]或[b,0]内能找到一个整数temp能同时被a和b所整除，则temp即为最大公约数。

③　更相减损法
1.任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。
2. 以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。

④　Stein算法
对两个正整数 x>y ：
1.均为偶数 gcd( x,y ) =2gcd( x/2,y/2 )；
2.均为奇数 gcd( x,y ) = gcd( (x+y)/2,(x-y)/2 )；
2.x奇y偶 gcd( x,y ) = gcd( x,y/2 )；
3.x偶y奇 gcd( x,y ) = gcd( x/2,y ) 或 gcd( x,y )=gcd( y,x/2 )；

⑤　求每段算法所用时间
将所需要计算时间的代码首尾进行标记，用clock()函数

三、算法构造

辗转相除法求最大公约数流程图

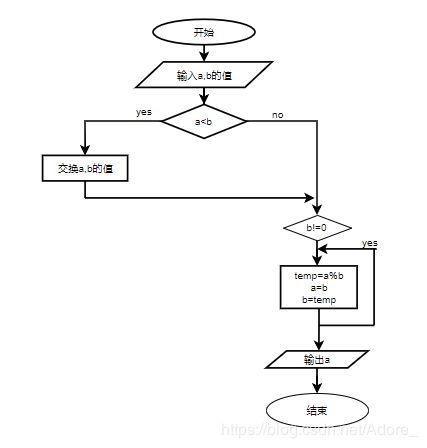
穷举法求最大公约数流程图

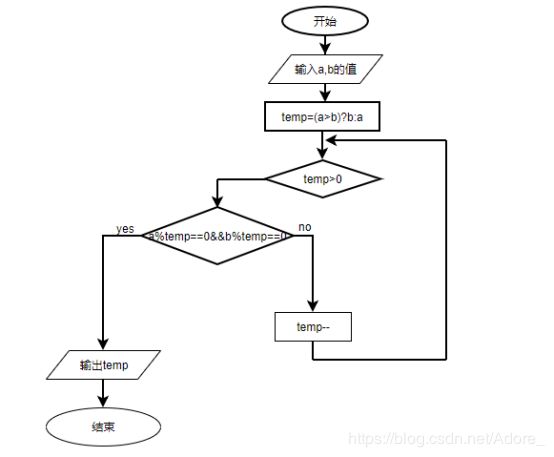
更相减损法求最大公约数流程图

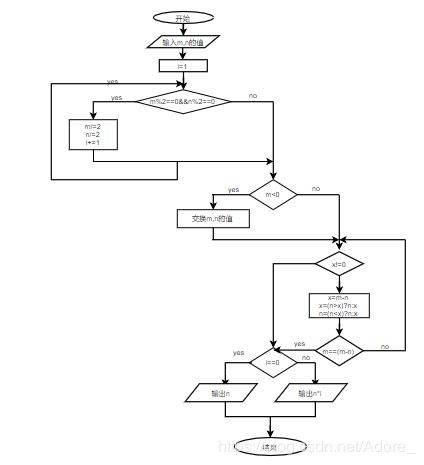
Stein算法求最大公约数流程图

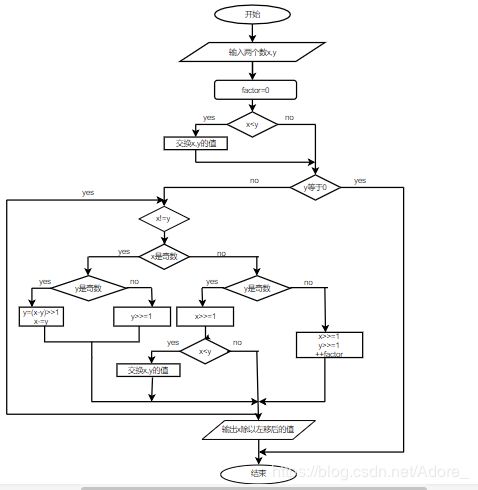
四、程序源代码

#include
#include  
#include 
#include
using namespace std;


 //辗转相除法
int divisor1(int a,int b)
{
	int temp;
	 if(ab)?b:a;//求出两数之间的最小值
	while(temp>0)
	{
		if(a%temp==0&&b%temp==0)  
			break;
		temp--;
	}
	return temp;
}

//更相减损法
int gcd(int a,int b)
{
	int i=0,temp,x;
	while(a%2==0 && b%2==0)  //判断m和n能被多少个2整除
	{
		a/=2;
		b/=2;
		i+=1;
	}
	if(ax)?b:x;
		b=(b> 1;
              x -= y;
            }
          else
               y >>= 1;
         }
        else
        {
           if ( y & 0x1 )
           {
               x >>= 1;
               if ( x < y )
               {temp = x;x = y;y = temp;}
             }
           else
           {
             x >>= 1;
             y >>= 1;
             ++factor;
             }
         }
     }
     return (x<

五、代码调试

对调用辗转相除法的一段代码进行调试，根据每一步，m,x,y,count,time,start,end的值，来分析代码是否正确。一共四块代码，其余也是这样。

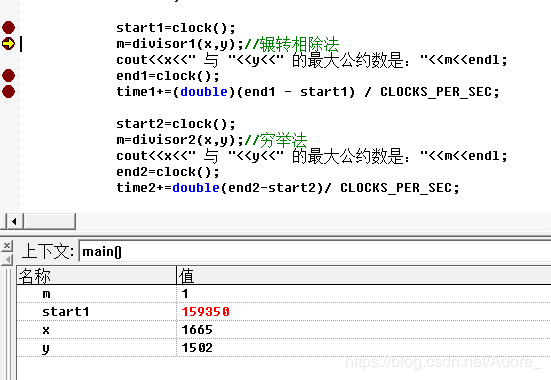
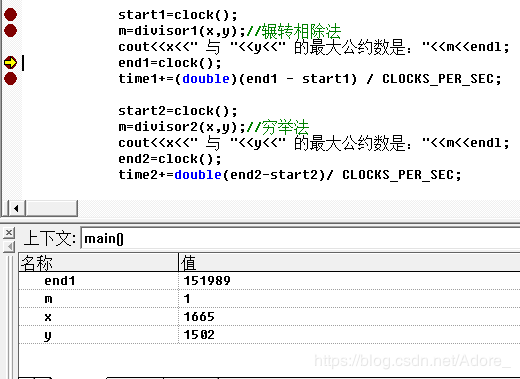
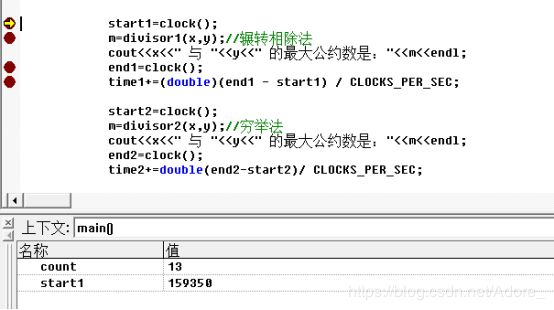
六、代码测试

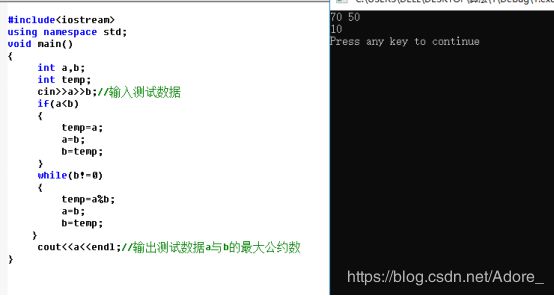
测试辗转相除法计算最大公约数

测试代码：

#include 
using namespace std;
void main()
{
	int temp;
	int a,b;
	cin>>a>>b;
	 if(a

测试穷举法计算最大公约数

测试代码：

#include 
using namespace std;
void main()
{
	int temp;
	int a,b;
	cin>>a>>b;
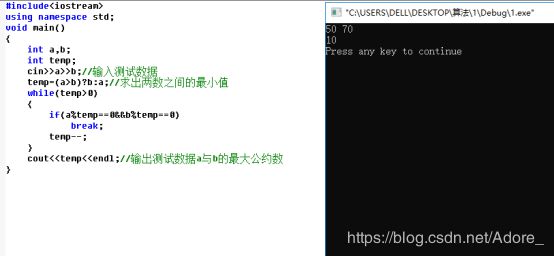
	temp=(a>b)?b:a;//求出两数之间的最小值
	while(temp>0)
	{
		if(a%temp==0&&b%temp==0)  
			break;
		temp--;
	}
	cout<

测试更相减损法计算最大公约数

测试代码：

#include 
#include
using namespace std;
void main()
{
	int i=0,temp,x;
	int a,b;
	cin>>a>>b;
	while(a%2==0 && b%2==0)  //判断m和n能被多少个2整除
	{
		a/=2;
		b/=2;
		i+=1;
	}
	if(ax)?b:x;
		b=(b

测试Stein算法计算最大公约数

测试代码：

#include 
using namespace std;
void main()
{
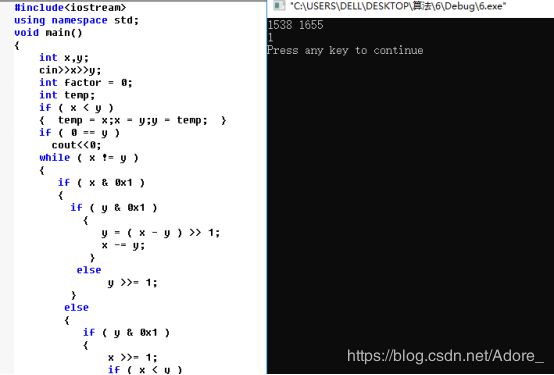
	int x,y;
	cin>>x>>y;
	int factor = 0;
    int temp;
	if ( x < y )
    {  temp = x;x = y;y = temp;  }
    if ( 0 == y )
      cout<<"输入错误";
    while ( x != y )
    {
       if ( x & 0x1 )
       {
         if ( y & 0x1 )
           {
              y = ( x - y ) >> 1;
              x -= y;
            }
          else
               y >>= 1;
         }
        else
        {
           if ( y & 0x1 )
           {
               x >>= 1;
               if ( x < y )
               {temp = x;x = y;y = temp;}
             }
           else
           {
             x >>= 1;
             y >>= 1;
             ++factor;
             }
         }
     }
     while(factor--)
		 x=x/2;
	 cout<

测试随机产生的20组数

测试代码：

#include 
#include
using namespace std;
void main()
{
	int count=0;
	int x,y;
	srand((unsigned)time(NULL));
	while(count<20)
	{
		x=rand()%1000+1000;  //随机产生100以内的数
		y=rand()%1000+1000;
		count++;
		cout<

七、运行结果

八、经验归纳

这次编程时，遇到两个问题:
1.首先，程序运行时，虽然是对20组随机数进行求取最大公约数，但是针对每种方法，那20组数据时不一样的。由于要比较四组算法的优劣性，可通过最终的时间大小比较。当是相同的数据时，比较才有意义。
2.产生随机数时，每次产生的随机数是一样的


将srand((unsigned)time(NULL));放在循环中时得到的随机数是相同的，通过调试，才知道这句要放在循环体外，改完后，可成功运行。