AES算法字节代换，行移位，列混淆，轮密钥加之例题详解+代码实现

AES算法学习记录

以下以一道例题论述AES算法中字节代换，行移位，列混淆，轮密钥加的一轮加密详细过程。

 

已知AES一轮迭代的输入为状态矩阵

{EA 04 65 85

 83 45 5D 96  

 5C 33 98 B0

 F0 2D AD C5},

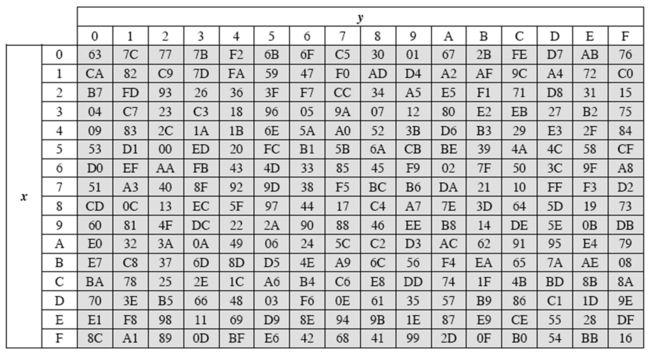
求一轮加密输出的第一个字节。期中列混淆矩阵、轮密钥、S盒分别为：

 

1.字节代换

字节代换较为简单，对照S盒进行代换即可

代换后的矩阵为：

91  D4  34  5B
F5  2D  3E  4A
33  86 A5   63
0D  FD  83  02

2.行移位

规则如下：

第一行保持不变，第二行循环左移8bit，第三行循环左移16bit，第四行循环左移24bit

图解（图片来源于网络^）：

假设矩阵为a，那么用方程表示为：a[i][j] = a[i][(i+j)%4]

于是可以得到行移位的代码：

int a[4][4] = {
    {0x91, 0xD4, 0x34, 0x5B},
    {0xF5, 0x2D, 0x3E, 0x4A},
    {0x33, 0x86, 0xA5, 0x63},
    {0x0D, 0xFD, 0x83, 0x02}
};
int b[4][4];//行移位后的矩阵

int main() {
    //行移位
    for(int i=0;i<=3;i++)
        for(int j=0;j<=3;j++)
            b[i][j] = a[i][(i+j)%4];
    for(int i=0;i<=3;i++) {
        for(int j=0;j<=3;j++) {
            cout<

得到行移位后的矩阵b为：

91 d4 34 5b
2d 3e 4a f5
a5 63 33 86
02 0d fd 83

2.列混淆

 

将矩阵b右乘列混淆矩阵，这个过程称为列混淆

即：

 

计算方式：

假设b矩阵某个数为x

x * 01，为x本身

x * 02，x的二进制左移一位（右边补0），如果溢出（即如果x的二进制最高位为1），那么再异或上 1B

x * 03，结果为 (x * 02) + x，即，先乘02再异或本身，计算方法和上面一样。

举例：

02 * 91

91的二进制位 1001 0001，左移一位得到 0010 0010，因为本身的二进制最高位为1，所以再异或本身 1001 0001即 

00100010 xor 10010001

得到 10110011 即：B3

核心算法代码（下有完整代码）

int mul_mat(int x,int y) {
    if(x == 0x01) {
        return y;
    }
    else if(x == 0x02) {
        if((y&128) != 128) { //二进制首位为0
            return y<<1;
        }
        else {
            int temp = ((y<<1)&((1<<8)-1)); //向左移一位，删掉最高位(保留8位)
            return temp^(0x1b);
        }
    }
    else if(x == 0x03) {
        return mul_mat(0x02,y)^y;
    }
}

得到列混淆后的矩阵为：

e9  9f  78  b7
3d  0    8   b8
eb  3b  4   27
24  20  c4  83

 

4.轮密钥加

用轮密钥矩阵的第 i 列，与上面得到的列混淆矩阵的第 i 列进行异或运算，得到最后的矩阵！

 

代码：

for(int i=0;i<=3;i++) {
        for(int j=0;j<=3;j++) {
            res[j][i] = resMix[j][i] ^ round_key[j][i];
        }
    }

 

 

整体代码：

#include
#include
#include
#include
#include
using namespace std;

int a[4][4] = {
    {0x91, 0xD4, 0x34, 0x5B},
    {0xF5, 0x2D, 0x3E, 0x4A},
    {0x33, 0x86, 0xA5, 0x63},
    {0x0D, 0xFD, 0x83, 0x02}
};//字节代换后的矩阵
int mixCol[4][4] = {
    {0x02, 0x03, 0x01, 0x01},
    {0x01, 0x02, 0x03, 0x01},
    {0x01, 0x01, 0x02, 0x03},
    {0x03, 0x01, 0x01, 0x02}
};//列混淆矩阵
int round_key[4][4] = {
    {0xAC, 0x19, 0x28, 0x57},
    {0x77, 0xFA, 0xD1, 0x5C},
    {0x66, 0xDC, 0x29, 0x00},
    {0xF3, 0x21, 0x41, 0x6A},
};//轮密钥矩阵

int b[4][4];//行移位后的矩阵
int resMix[4][4];//列混淆后的矩阵
int res[4][4];//轮密钥加后的矩阵

int mul_mat(int x,int y) {
    if(x == 0x01) {
        return y;
    }
    else if(x == 0x02) {
        if((y&128) != 128) { //二进制首位为0
            return y<<1;
        }
        else {
            int temp = ((y<<1)&((1<<8)-1)); //向左移一位，删掉最高位(保留8位)
            return temp^(0x1b);
        }
    }
    else if(x == 0x03) {
        return mul_mat(0x02,y)^y;
    }
}


int main() {

    cout<<"字节代换后的矩阵为："<