Python实现马科维茨有效边界

Python实现马科维茨有效边界

参考文章

1. https://mp.weixin.qq.com/s/neCSaWK0c4jzWwCfDVFA6A
2. https://mp.weixin.qq.com/s/2X_VCZwv8EX4S48wAeL0AQ

导入包

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tushare as ts
import scipy.optimize as sco

获取股票数据

原文章中是用美股数据实现的，我试着用沪深的数据实现一下，通过tuhsare来获取选定股票的日收益率。我挑了5只股票：贵州茅台（600519）、格力电器（000651）、万科A（000002）、中国平安（601318）、中国石油（601857）

df = pd.DataFrame()
df = ts.get_hist_data('600519', start='2015-01-05', end='2018-12-28') 
s600519 = df['p_change']
s600519.name = '600519'

df = pd.DataFrame()
df = ts.get_hist_data('000651', start='2015-01-05', end='2018-12-28') 
s000651 = df['p_change']
s000651.name = '000651'

df = pd.DataFrame()
df = ts.get_hist_data('000002', start='2015-01-05', end='2018-12-28') 
s000002 = df['p_change']
s000002.name = '000002'

df = pd.DataFrame()
df = ts.get_hist_data('601318', start='2015-01-05', end='2018-12-28') 
s601318 = df['p_change']
s601318.name = '601318'

df = pd.DataFrame()
df = ts.get_hist_data('601857', start='2015-01-05', end='2018-12-28') 
s601857 = df['p_change']
s601857.name = '601857'

data = pd.DataFrame({'600519':s600519,'000651':s000651,'000002':s000002, '601318':s601318,'601857':s601857})
data = data.dropna()

计算年化收益率和协方差矩阵（以一年252个交易日计算）

returns_annual = data.mean() * 252
cov_annual = data.cov() * 252

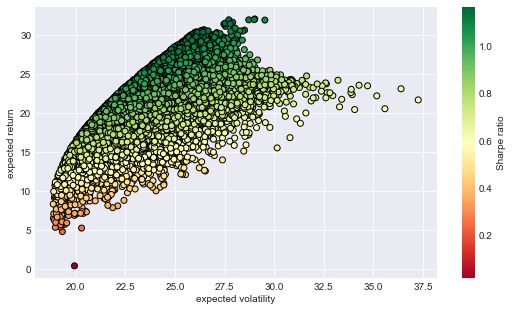
模拟投资组合

为了得到有效边界，我们模拟了50000个投资组合

number_assets = 5
weights = np.random.random(number_assets)
weights /= np.sum(weights)

portfolio_returns = []
portfolio_volatilities = []
sharpe_ratio = []
for single_portfolio in range (50000):
      weights = np.random.random(number_of_assets)
      weights /= np.sum(weights) 
      returns = np.dot(weights, returns_annual)
      volatility = np.sqrt(np.dot(weights.T, np.dot(cov_annual, weights)))
      portfolio_returns.append(returns)
      portfolio_volatilities.append(volatility)
      sharpe = returns / volatility
      sharpe_ratio.append(sharpe)

portfolio_returns = np.array(portfolio_returns)
portfolio_volatilities = np.array(portfolio_volatilities)

作图

plt.style.use('seaborn-dark')
plt.figure(figsize=(9, 5))
plt.scatter(portfolio_volatilities, portfolio_returns, c=sharpe_ratio,cmap='RdYlGn', edgecolors='black',marker='o') 
plt.grid(True)
plt.xlabel('expected volatility')
plt.ylabel('expected return')
plt.colorbar(label='Sharpe ratio')

得到马科维茨有效边界如下

找出最优组合

def statistics(weights):        
    weights = np.array(weights)
    pret = np.sum(data.mean() * weights) * 252
    pvol = np.sqrt(np.dot(weights.T, np.dot(data.cov() * 252, weights)))
    return np.array([pret, pvol, pret / pvol])

def min_func_sharpe(weights):
    return -statistics(weights)[2]

bnds = tuple((0, 1) for x in range(number_assets))
cons = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
opts = sco.minimize(min_func_sharpe, number_assets * [1. / number_assets,], method='SLSQP',  bounds=bnds, constraints=cons)
opts['x'].round(3)  #得到各股票权重
statistics(opts['x']).round(3)  #得到投资组合预期收益率、预期波动率以及夏普比率

输出结果为

In [5]: opts['x'].round(3)
Out[5]: array([0.561, 0.   , 0.06 , 0.38 , 0.   ])

In [6]: statistics(opts['x']).round(3)
Out[6]: array([31.102, 26.485,  1.174])

可以得出最优投资组合（夏普比率最高）为买入56.1%的资金买入贵州茅台（600519）、6%的资金买入万科A（000002）、38%的资金买入中国平安（601318）
其期望收益率为31.10%，期望波动率为26.49%

完整代码

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import tushare as ts
import scipy.optimize as sco

df = pd.DataFrame()
df = ts.get_hist_data('600519', start='2015-01-05', end='2018-12-28') 
s600519 = df['p_change']
s600519.name = '600519'

df = pd.DataFrame()
df = ts.get_hist_data('000651', start='2015-01-05', end='2018-12-28') 
s000651 = df['p_change']
s000651.name = '000651'

df = pd.DataFrame()
df = ts.get_hist_data('000002', start='2015-01-05', end='2018-12-28') 
s000002 = df['p_change']
s000002.name = '000002'

df = pd.DataFrame()
df = ts.get_hist_data('601318', start='2015-01-05', end='2018-12-28') 
s601318 = df['p_change']
s601318.name = '601318'

df = pd.DataFrame()
df = ts.get_hist_data('601857', start='2015-01-05', end='2018-12-28') 
s601857 = df['p_change']
s601857.name = '601857'

data = pd.DataFrame({'600519':s600519,'000651':s000651,'000002':s000002, '601318':s601318,'601857':s601857})
data = data.dropna()

returns_annual = data.mean() * 252
cov_annual = data.cov() * 252

number_assets = 5
weights = np.random.random(number_assets)
weights /= np.sum(weights)

portfolio_returns = []
portfolio_volatilities = []
sharpe_ratio = []
for single_portfolio in range (50000):
      weights = np.random.random(number_of_assets)
      weights /= np.sum(weights) 
      returns = np.dot(weights, returns_annual)
      volatility = np.sqrt(np.dot(weights.T, np.dot(cov_annual, weights)))
      portfolio_returns.append(returns)
      portfolio_volatilities.append(volatility)
      sharpe = returns / volatility
      sharpe_ratio.append(sharpe)

portfolio_returns = np.array(portfolio_returns)
portfolio_volatilities = np.array(portfolio_volatilities)

plt.style.use('seaborn-dark')
plt.figure(figsize=(9, 5))
plt.scatter(portfolio_volatilities, portfolio_returns, c=sharpe_ratio,cmap='RdYlGn', edgecolors='black',marker='o') 
plt.grid(True)
plt.xlabel('expected volatility')
plt.ylabel('expected return')
plt.colorbar(label='Sharpe ratio')

def statistics(weights):        
    weights = np.array(weights)
    pret = np.sum(data.mean() * weights) * 252
    pvol = np.sqrt(np.dot(weights.T, np.dot(data.cov() * 252, weights)))
    return np.array([pret, pvol, pret / pvol])

def min_func_sharpe(weights):
    return -statistics(weights)[2]

bnds = tuple((0, 1) for x in range(number_assets))
cons = ({'type': 'eq', 'fun': lambda x: np.sum(x) - 1})
opts = sco.minimize(min_func_sharpe, number_assets * [1. / number_assets,], method='SLSQP',  bounds=bnds, constraints=cons)
opts['x'].round(3)  #得到各股票权重
statistics(opts['x']).round(3)  #得到投资组合预期收益率、预期波动率以及夏普比率