挖掘建模

一、分类与预测

分类和预测是预测问题的两种主要类型，分类主要是预测分类标号（离散属性），而预测主要是建立连续值函数模型，预测给定自变量对应因变量的值。
1.主要分类与预测算法
回归分析
决策树
人工神经网络
贝叶斯网络
支持向量机
2.回归分析
回归分析是通过建立模型来研究变量之间相互关系的密切程度、结构状态以及进行模型预测的一种有效工具。
1. 线性回归：因变量和自变量是线性关系
2. 非线性回归：因变量和自变量不都是线性关系
3. logistic回归：因变量一般有1和0（是否）两种取值
4. 岭回归：参与建模的自变量之间具有多重共线性
5. 主成分回归：参与建模的自变量之间具有多重共线性

logical回归：

逻辑回归 自动建模
import pandas as pd

#参数初始化
filename = '../data/bankloan.xls'
data = pd.read_excel(filename)
x = data.iloc[:,:8].as_matrix()
y = data.iloc[:,8].as_matrix()

from sklearn.linear_model import LogisticRegression as LR
from sklearn.linear_model import RandomizedLogisticRegression as RLR
rlr = RLR() #建立随机逻辑回归模型，筛选变量
rlr.fit(x, y) #训练模型
rlr.get_support() #获取特征筛选结果，也可以通过.scores_方法获取各个特征的分数
print(u'通过随机逻辑回归模型筛选特征结束。')
print(u'有效特征为：%s' % ','.join(data.columns[rlr.get_support()]))
x = data[data.columns[rlr.get_support()]].as_matrix() #筛选好特征

lr = LR() #建立逻辑货柜模型
lr.fit(x, y) #用筛选后的特征数据来训练模型
print(u'逻辑回归模型训练结束。')
print(u'模型的平均正确率为：%s' % lr.score(x, y)) #给出模型的平均正确率，本例为81.4%

运行结果：

有效特征为：工龄,地址,负债率,信用卡负债
逻辑回归模型训练结束。
模型的平均正确率为：0.814285714286
3.决策树
代码：

#-*- coding: utf-8 -*-
#使用ID3决策树算法预测销量高低
import pandas as pd

#参数初始化
inputfile = '../data/sales_data.xls'
data = pd.read_excel(inputfile, index_col = u'序号') #导入数据

#数据是类别标签，要将它转换为数据
#用1来表示“好”、“是”、“高”这三个属性，用-1来表示“坏”、“否”、“低”
data[data == u'好'] = 1
data[data == u'是'] = 1
data[data == u'高'] = 1
data[data != 1] = -1
x = data.iloc[:,:3].as_matrix().astype(int)
y = data.iloc[:,3].as_matrix().astype(int)

from sklearn.tree import DecisionTreeClassifier as DTC
dtc = DTC(criterion='entropy') #建立决策树模型，基于信息熵
dtc.fit(x, y) #训练模型

#导入相关函数，可视化决策树。
#导出的结果是一个dot文件，需要安装Graphviz才能将它转换为pdf或png等格式。
from sklearn.tree import export_graphviz
x = pd.DataFrame(x)
from sklearn.externals.six import StringIO
x = pd.DataFrame(x)
with open("tree.dot", 'w') as f:
  f = export_graphviz(dtc, feature_names = x.columns, out_file = f)

运行结果：
生成的dot文件如下：

digraph Tree {
edge [fontname="SimHei"];
node [fontname="SimHei"];
node [shape=box] ;
0 [label="1 <= 0.0\nentropy = 0.9975\nsamples = 34\nvalue = [16, 18]"] ;
1 [label="2 <= 0.0\nentropy = 0.9341\nsamples = 20\nvalue = [13, 7]"] ;
0 -> 1 [labeldistance=2.5, labelangle=45, headlabel="True"] ;
2 [label="0 <= 0.0\nentropy = 0.5436\nsamples = 8\nvalue = [7, 1]"] ;
1 -> 2 ;
3 [label="entropy = 0.0\nsamples = 4\nvalue = [4, 0]"] ;
2 -> 3 ;
4 [label="entropy = 0.8113\nsamples = 4\nvalue = [3, 1]"] ;
2 -> 4 ;
5 [label="0 <= 0.0\nentropy = 1.0\nsamples = 12\nvalue = [6, 6]"] ;
1 -> 5 ;
6 [label="entropy = 0.971\nsamples = 5\nvalue = [3, 2]"] ;
5 -> 6 ;
7 [label="entropy = 0.9852\nsamples = 7\nvalue = [3, 4]"] ;
5 -> 7 ;
8 [label="0 <= 0.0\nentropy = 0.7496\nsamples = 14\nvalue = [3, 11]"] ;
0 -> 8 [labeldistance=2.5, labelangle=-45, headlabel="False"] ;
9 [label="2 <= 0.0\nentropy = 0.9544\nsamples = 8\nvalue = [3, 5]"] ;
8 -> 9 ;
10 [label="entropy = 0.9183\nsamples = 3\nvalue = [2, 1]"] ;
9 -> 10 ;
11 [label="entropy = 0.7219\nsamples = 5\nvalue = [1, 4]"] ;
9 -> 11 ;
12 [label="entropy = 0.0\nsamples = 6\nvalue = [0, 6]"] ;
8 -> 12 ;
}

下载Graphviz绘图：
生成图片格式代码：
建立bat文件，写入

set dotPath=D:\hh
set sourcePath=d:\Users\baobao\Desktop
%dotPath%\bin\dot.exe -Tjpg %sourcePath%\tree.dot -o %sourcePath%\tree.jpg
pause

运行结果为：

4.人工神经网络
人工神经元模型

神经网络算法代码：

#-*- coding: utf-8 -*-
#使用神经网络算法预测销量高低

import pandas as pd

#参数初始化
inputfile = '../data/sales_data.xls'
data = pd.read_excel(inputfile, index_col = u'序号') #导入数据

#数据是类别标签，要将它转换为数据
#用1来表示“好”、“是”、“高”这三个属性，用0来表示“坏”、“否”、“低”
data[data == u'好'] = 1
data[data == u'是'] = 1
data[data == u'高'] = 1
data[data != 1] = 0
x = data.iloc[:,:3].as_matrix().astype(int)
y = data.iloc[:,3].as_matrix().astype(int)

from keras.models import Sequential
from keras.layers.core import Dense, Activation

model = Sequential() #建立模型
model.add(Dense(input_dim = 3, output_dim = 10))
model.add(Activation('relu')) #用relu函数作为激活函数，能够大幅提供准确度
model.add(Dense(input_dim = 10, output_dim = 1))
model.add(Activation('sigmoid')) #由于是0-1输出，用sigmoid函数作为激活函数

model.compile(loss = 'binary_crossentropy', optimizer = 'adam', class_mode = 'binary')
#编译模型。由于我们做的是二元分类，所以我们指定损失函数为binary_crossentropy，以及模式为binary
#另外常见的损失函数还有mean_squared_error、categorical_crossentropy等，请阅读帮助文件。
#求解方法我们指定用adam，还有sgd、rmsprop等可选

model.fit(x, y, nb_epoch = 1000, batch_size = 10) #训练模型，学习一千次
yp = model.predict_classes(x).reshape(len(y)) #分类预测

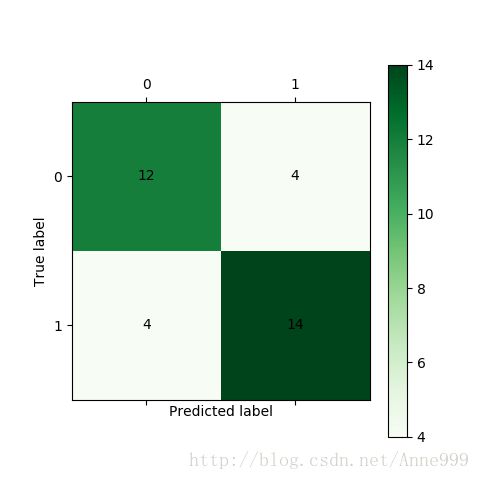
from cm_plot import * #导入自行编写的混淆矩阵可视化函数
cm_plot(y,yp).savefig("/home/python/syy/images/pi5_11.png") #显示混淆矩阵可视化结果

画图自定义：

# -*- coding: utf-8 -*-
def cm_plot(y, yp):
    from sklearn.metrics import confusion_matrix  # 导入混淆矩阵函数

    cm = confusion_matrix(y, yp)  # 混淆矩阵

    import matplotlib.pyplot as plt  # 导入作图库
    plt.matshow(cm, cmap=plt.cm.Greens)  # 画混淆矩阵图，配色风格使用cm.Greens，更多风格请参考官网。
    plt.colorbar()  # 颜色标签

    for x in range(len(cm)):  # 数据标签
        for y in range(len(cm)):
            plt.annotate(cm[x, y], xy=(x, y), horizontalalignment='center', verticalalignment='center')

    plt.ylabel('True label')  # 坐标轴标签
    plt.xlabel('Predicted label')  # 坐标轴标签
    return plt

混淆矩阵图：

二、聚类分析

1.k-means算法

#-*- coding: utf-8 -*-
#使用K-Means算法聚类消费行为特征数据

import pandas as pd

#参数初始化
inputfile = '../data/consumption_data.xls' #销量及其他属性数据
outputfile = '../tmp/data_type.xls' #保存结果的文件名
k = 3 #聚类的类别
iteration = 500 #聚类最大循环次数
data = pd.read_excel(inputfile, index_col = 'Id') #读取数据
data_zs = 1.0*(data - data.mean())/data.std() #数据标准化

from sklearn.cluster import KMeans
model = KMeans(n_clusters = k, n_jobs = 4, max_iter = iteration) #分为k类，并发数4
model.fit(data_zs) #开始聚类

#简单打印结果
r1 = pd.Series(model.labels_).value_counts() #统计各个类别的数目
r2 = pd.DataFrame(model.cluster_centers_) #找出聚类中心
r = pd.concat([r2, r1], axis = 1) #横向连接（0是纵向），得到聚类中心对应的类别下的数目
r.columns = list(data.columns) + [u'类别数目'] #重命名表头
print(r)

#详细输出原始数据及其类别
r = pd.concat([data, pd.Series(model.labels_, index = data.index)], axis = 1)  #详细输出每个样本对应的类别
r.columns = list(data.columns) + [u'聚类类别'] #重命名表头
r.to_excel(outputfile) #保存结果

输出结果：
R F M 类别数目
0 -0.160451 1.114802 0.392844 341
1 -0.149353 -0.658893 -0.271780 559
2 3.455055 -0.295654 0.449123 40
数据：

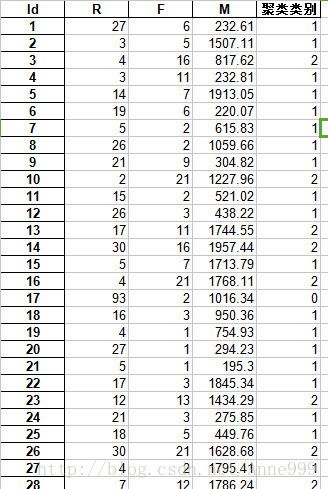
不同客户群密度图：

def density_plot(data): #自定义作图函数
  import matplotlib.pyplot as plt
  plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
  plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
  p = data.plot(kind='kde', linewidth = 2, subplots = True, sharex = False)
  [p[i].set_ylabel(u'Density') for i in range(k)]
  plt.legend()
  return plt

pic_output = '../tmp/pd_' #概率密度图文件名前缀
for i in range(k):
  density_plot(data[r[u'聚类类别']==i]).savefig(u'%s%s.png' %(pic_output, i))

分群1概率密度图：

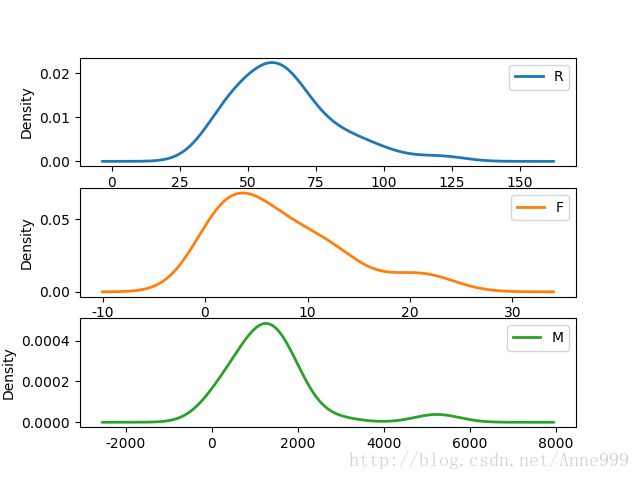
分群2概率密度图：

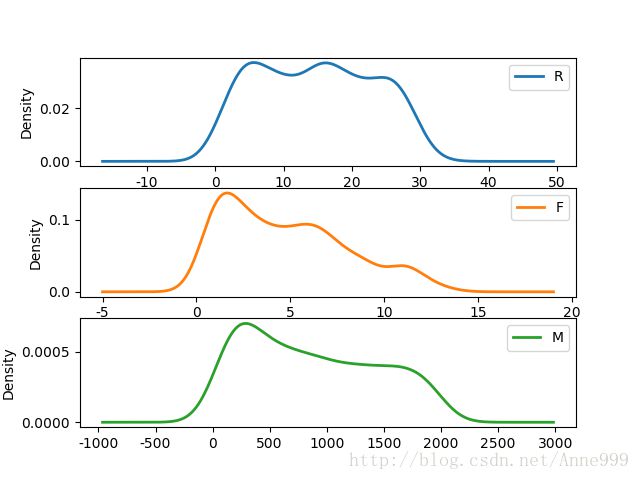
分群3概率密度图：

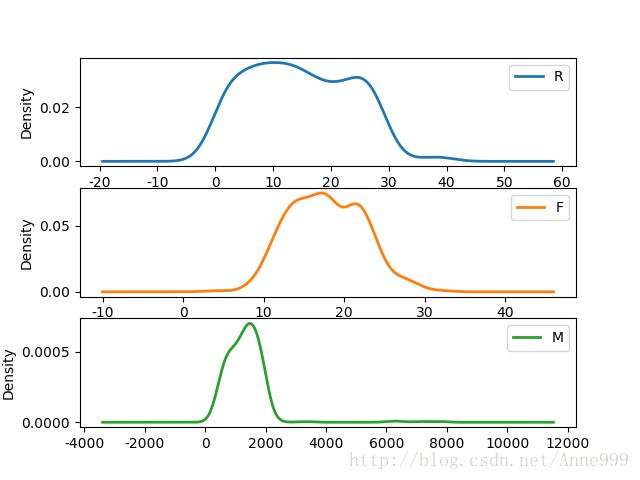
可以看出分群3是价值低的客户。

三、关联规则

1.常用关联规则算法
Apriori
FP-Tree
Eclat算法
灰色关联法
2.Apriori

#-*- coding: utf-8 -*-
#使用Apriori算法挖掘菜品订单关联规则
from __future__ import print_function
import pandas as pd
from apriori import * #导入自行编写的apriori函数

inputfile = '../data/menu_orders.xls'
outputfile = '../tmp/apriori_rules.xls' #结果文件
data = pd.read_excel(inputfile, header = None)

print(u'\n转换原始数据至0-1矩阵...')
ct = lambda x : pd.Series(1, index = x[pd.notnull(x)]) #转换0-1矩阵的过渡函数
b = map(ct, data.as_matrix()) #用map方式执行
data = pd.DataFrame(list(b)).fillna(0) #实现矩阵转换，空值用0填充
print(u'\n转换完毕。')
del b #删除中间变量b，节省内存

support = 0.2 #最小支持度
confidence = 0.5 #最小置信度
ms = '---' #连接符，默认'--'，用来区分不同元素，如A--B。需要保证原始表格中不含有该字符

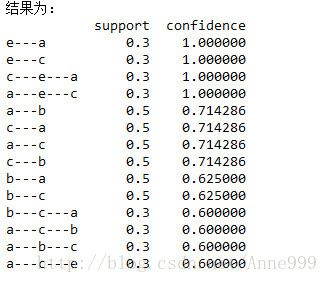
find_rule(data, support, confidence, ms).to_excel(outputfile) #保存结果

四、时序模型

1.时间序列算法：
平滑法
趋势拟合法
组合模型
AR模型·
MA模型
ARMA模型
ARIMA模型
ARCH模型
GARCH模型
2.时间序列预处理
首先进行纯随机性和平稳性检验，对于纯随机序列，又称白噪声序列，序列的各项之间没有任何关系，在进行中完全无序随机波动，可以终止对该序列的分析。对于平稳的白噪声序列，均值和方差是常数，可以建立模型。对于非平稳序列，转换为平稳序列。
3.ARIMA模型
代码：

#-*- coding: utf-8 -*-
#arima时序模型

import pandas as pd

#参数初始化
discfile = '../data/arima_data.xls'
forecastnum = 5

#读取数据，指定日期列为指标，Pandas自动将“日期”列识别为Datetime格式
data = pd.read_excel(discfile, index_col = u'日期')

#时序图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
data.plot()
plt.savefig("../tmp/pic1.png")

#自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data).savefig("../tmp/pic2.png")

#平稳性检测
from statsmodels.tsa.stattools import adfuller as ADF
print(u'原始序列的ADF检验结果为：', ADF(data[u'销量']))
#返回值依次为adf、pvalue、usedlag、nobs、critical values、icbest、regresults、resstore

#差分后的结果
D_data = data.diff().dropna()
D_data.columns = [u'销量差分']
D_data.plot() #时序图
plt.savefig("../tmp/pic3.png")
plot_acf(D_data).show() #自相关图
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(D_data).savefig("../tmp/pic4.png") #偏自相关图
print(u'差分序列的ADF检验结果为：', ADF(D_data[u'销量差分'])) #平稳性检测

#白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
print(u'差分序列的白噪声检验结果为：', acorr_ljungbox(D_data, lags=1)) #返回统计量和p值

from statsmodels.tsa.arima_model import ARIMA

data[u'销量'] = data[u'销量'].astype(float)
#定阶
pmax = int(len(D_data)/10) #一般阶数不超过length/10
qmax = int(len(D_data)/10) #一般阶数不超过length/10
bic_matrix = [] #bic矩阵
for p in range(pmax+1):
  tmp = []
  for q in range(qmax+1):
    try: #存在部分报错，所以用try来跳过报错。
      tmp.append(ARIMA(data, (p,1,q)).fit().bic)
    except:
      tmp.append(None)
  bic_matrix.append(tmp)

bic_matrix = pd.DataFrame(bic_matrix) #从中可以找出最小值

p,q = bic_matrix.stack().idxmin() #先用stack展平，然后用idxmin找出最小值位置。
print(u'BIC最小的p值和q值为：%s、%s' %(p,q)) 
model = ARIMA(data, (p,1,q)).fit() #建立ARIMA(0, 1, 1)模型
model.summary2() #给出一份模型报告
model.forecast(5) #作为期5天的预测，返回预测结果、标准误差、置信区间。

结果分析：
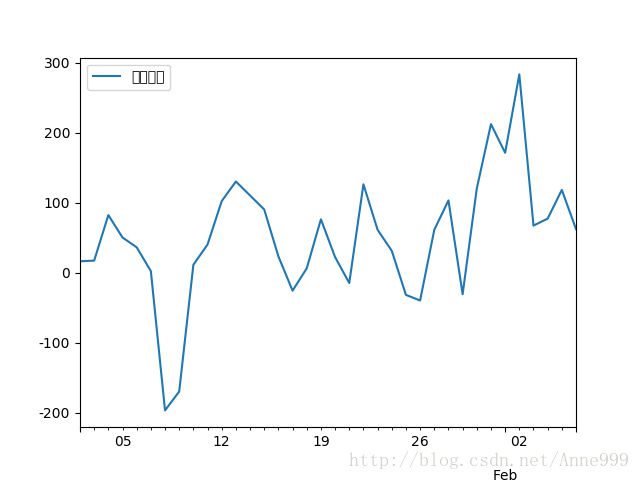
原始序列时序图

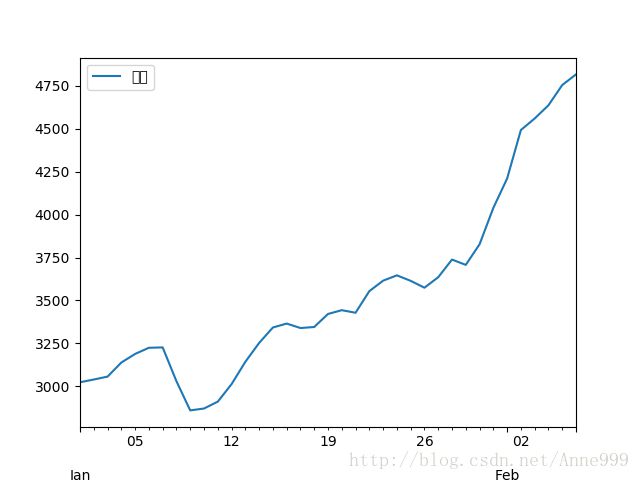
原始序列自相关图：

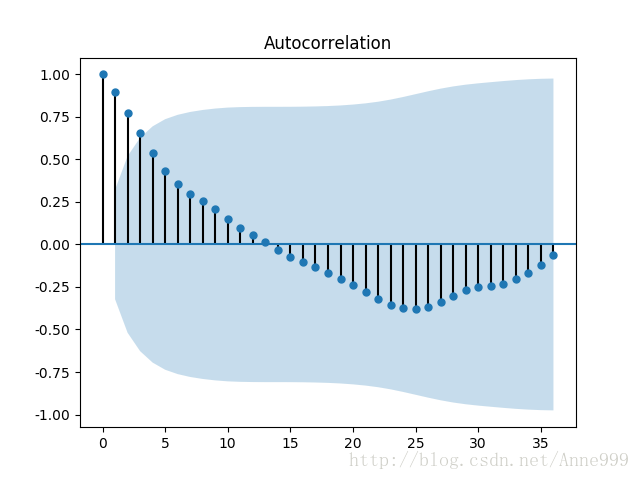
一阶差分后：

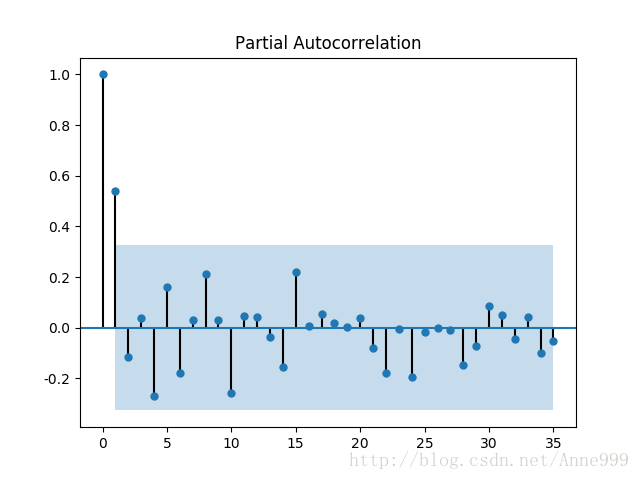
五、离群检测点

1.离散点检测

#-*- coding: utf-8 -*-
#使用K-Means算法聚类消费行为特征数据

import numpy as np
import pandas as pd

#参数初始化
inputfile = '../data/consumption_data.xls' #销量及其他属性数据
k = 3 #聚类的类别
threshold = 2 #离散点阈值
iteration = 500 #聚类最大循环次数
data = pd.read_excel(inputfile, index_col = 'Id') #读取数据
data_zs = 1.0*(data - data.mean())/data.std() #数据标准化

from sklearn.cluster import KMeans
model = KMeans(n_clusters = k, n_jobs = 4, max_iter = iteration) #分为k类，并发数4
model.fit(data_zs) #开始聚类

#标准化数据及其类别
r = pd.concat([data_zs, pd.Series(model.labels_, index = data.index)], axis = 1)  #每个样本对应的类别
r.columns = list(data.columns) + [u'聚类类别'] #重命名表头

norm = []
for i in range(k): #逐一处理
  norm_tmp = r[['R', 'F', 'M']][r[u'聚类类别'] == i]-model.cluster_centers_[i]
  norm_tmp = norm_tmp.apply(np.linalg.norm, axis = 1) #求出绝对距离
  norm.append(norm_tmp/norm_tmp.median()) #求相对距离并添加

norm = pd.concat(norm) #合并

import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False #用来正常显示负号
norm[norm <= threshold].plot(style = 'go') #正常点

discrete_points = norm[norm > threshold] #离群点
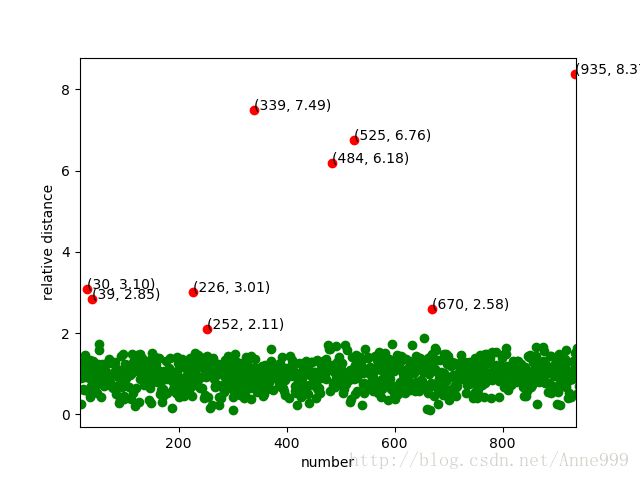
discrete_points.plot(style = 'ro')

for i in range(len(discrete_points)): #离群点做标记
  id = discrete_points.index[i]
  n = discrete_points.iloc[i]
  plt.annotate('(%s, %0.2f)'%(id, n), xy = (id, n), xytext = (id, n))

plt.xlabel(u'number')
plt.ylabel(u'relative distance')
plt.savefig("../tmp/pic111.png")