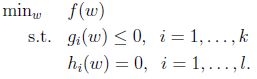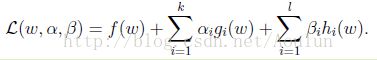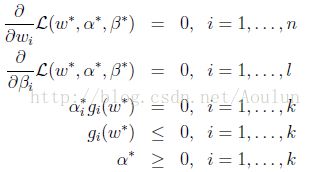支持向量机与支持向量回归(support vector machine and support vector regression)
支持向量机和支持向量回归是目前机器学习领域用得较多的方法,不管是人脸识别,字符识别,行为识别,姿态识别等,都可以看到它们的影子。在我的工作中,经常用到支持向量机和支持向量回归,然而,作为基本的理论,却没有认真地去梳理和总结,导致有些知识点没有彻底的弄明白。这篇博客主要就是想梳理一遍支持向量机和支持向量回归的基础理论知识,一个是笔记,另一个是交流学习,便于大家共勉。
凸集、凸函数、凸优化
凸集:如果集合中任意两点之间连线上的点都在集合中,那么这个集合就是凸集。常见凸集:n维实数空间;仿射子空间;凸集的交集;n维半正定矩阵集。
凸函数:几何意义为函数任意两点连线上的值都大于对应的自变量处函数的值。常见凸函数:指数函数族;非负对数函数;仿射函数;二次函数;常见的范数函数;凸函数非负加权的和。
凸优化:目标函数是凸函数,变量所属集合是凸集合的优化问题,或者目标函数是凸函数,变量的约束函数凸函数(不等式约束时),或者仿射函数(等式约束时)。例如,线性规划。
为什么要强调目标函数是凸函数或者凹函数呢,因为凸函数的局部极小值就是全局最小值,而凹函数的局部最大值就是全局最大值。所以,当采用适当的方法逼近局部极小值或者局部极大值时,也就是逼近全局最小值或者全局最大值。
拉格朗日对偶性(浅显的理解)
拉个朗日对偶性:将求解某一类最优化(如最小化)问题,转换为求解另一种最优化(如最大化)问题。这样的好处是:使得问题的求解更容易。
例子
个人绝对对于数学专业的来说,肯定要搞清楚来龙去脉,但是这就有点绕了。所以我们需要直接的感官理解才行。
(公式都是借用的)
求解如下的有不等式约束(等式约束的最小化问题可以直接用高中学的求导方法求解)的最小化优化问题:
引入拉格朗日函数(这里要求ai为非负的):
那么如何将这个拉格朗日函数与之前的f(w)等价起来呢?
首先看下面的优化问题:
当w固定时,如果在w固定时,gi(w)>0或者hi(w)不等于0,那么此时,总可以找到alpha 和 贝塔的值,使得公式(2)的值为无穷大。而只有在w固定,gi(w)和hi(w)满足原始的约束条件时,公式(2)的值才为f(w).因此,也可以表示为:
那么,既然在满足约束条件时,公式(2)的结果与f(w)是等价的,那么原始的求解最小化问题,就转化为公式(3)(因为公式(3)中的max{}值就是f(w)):
如果直接求解这个问题会很复杂,那么此时就引入对偶问题,当满足一定的条件时,对偶问题的解,就是公式(3)的解。
对偶问题的构造过程如下:
构造函数:![]()
将此拉格朗日函数转换为alpha 和 贝塔的函数,并求最大值
公式(4)就是公式(3)的对偶问题。然而,两个公式的值并不是相同的,
只有满足如下的条件时,两者的解才是相同的,也就是KKT条件。
KKT描述如下:
假设函数f(w)和g(w)是凸函数,h(w)是仿射函数,并且假定不等式约束g(w)是严格可行的,也即存在w,满足所有的不等式约束,则原始问题和对偶问题有解,并且解相同。其解相同的充要条件是解满足KKT条件:
函数间隔与几何间隔
上面我们定义类的标签只有0和1,但是,由于历史原因,以及便于理解和计算方便,我们将类标签定义为-1和1.(详细的讨论可以参考本文末尾的参考博客)
为什么要说函数间隔与几何间隔呢,因为函数间隔与几何间隔是理解分类的两个重要概念。
对于线性分类问题(可以参考我的博客:线性回归与梯度下降),目的是就得到分类的函数f(x)=wx+b;w就是上文中的theta,b就是不包含特征的一个常量。对于二分类问题,例如上面的-1和1两个类标签,如果f(x)的值是大于0,则分到1这个类,如果f(x)小于0,就分到-1这个类。这里可以很明显的看到,如果每个样本都正确的分到所有的类别后,用类别的标签乘以f(x)就必然是大于0的(很神奇),用公式表示为(用y来表示类别的标签,取值为-1和1):y*f(x)>0。
此时,我们定义y*f(x)就是函数间隔。(实际上,|wx+b|可以看作任意一个样本点离wx+b=0这个点的距离,因为wx+b=0这个样本点不属于任何类,刚好把其他的样本点分成两类。此时,定义f(x)=wx+b=0就是分类的超平面,注意f(x)=0中的0不要和类标签的0混淆。)
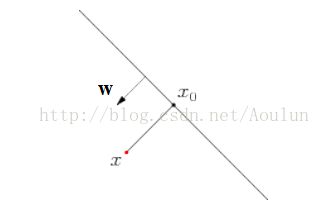
然而,这个函数间隔会随着w和b值的变化而变化,例如w和b成比例的增加,那么函数间隔也会成比例的增加。然而,我们在分类的时候,希望f(x)的值是>>0或者<<0,如果用函数间隔的话,那就意味着,当w和b的值改变,使得f(x)的值增加了,使得那些本身就很模棱两可的样本点就因为距离的改变分到了某个类。一个可行的办法是归一化处理,就是不管w和b的值如何改变,都不影响间隔大小。我们用下面的图来说明,w是图中分类直线的法向量,样本点x到分类直线的垂直投影为x0,x到x0距离为L,则:
x = x0 + w/||w||. (5)
实际上,上面的公式(5)就可以表示为:f(x)/||w||,同样的如果乘以类别标签,则变为:yf(x)/||w||,称这个函数就是几何间隔。
支持向量
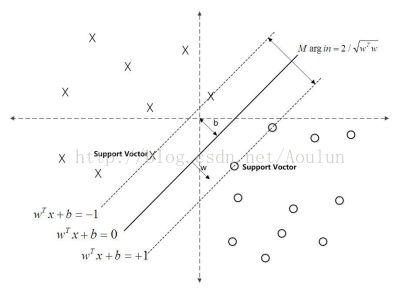
首先来看看这个二分类的问题,如下图,
对于而分类的问题,如果一个样本点离分类的超平面(wx+b=0)的距离越远,那么分类的确信度也就越高,因为f(x)>>0,或者f(x)<<0,就可以确定分类的准确性。所以,我们希望所有的样本点都满足这个条件。但是,举个例子来说明,对于标签为1的类,如果所有的样本点到超平面的距离(几何间隔)都很远,那么我们可以确定这些样本点都是标签为1的类。然而,并不是所有的样本点到超平面的几何距离都很远,那怎么办呢,我们就只需要这些样本点中到超平面的距离中最近的点最大不就行了吗。为了方便,用公式来说明:
对于所有的样本点,几何间隔为yi(wxi + b) ;为了便于计算,令样本点中离超平面最短的样本点其函数间隔为1,即f(x)=1,则分类的优化问题就可以描述为:
max(1/||w||), s.t. yi(wxi + b)>1(因为最短的函数间隔为1,所以所有的样本点起函数间隔必然大于1); (6)
如上图所示,在虚线上的点就是支持向量,因为它们刚好在边界上。
支持向量回归
分类:比如说有一大堆数据,我想把这些数据分开,比如说分成两个类、三个类等。比如说SVM,目的是使得两个类的所有数据离分类面最远,或者两个类的支持向量离分类面最远。
支持向量机分类
为什么要有核函数
SVM是解决线性可分问题的。
但是在有些情况下遇到的分类问题中,并不能找到这个线性可分的分类面。所以,通常就把这些数据映射到高维的空间,在这个高维空间找到线性可分的分类面。最后把高维的分类面映射回低维,就可以在低维空间对数据分类的。而映射回来后,低维的分类面就是一个非线性的分类面。但是,将低维的数据映射到高维,在高维做计算的话,计算量往往是很大的,尤其表现在当维度很高的情况下,例如(x,y,z,c,d,e,f)等等这样的维度。因此,核函数就来了。核函数就是在低维时,就对数据进行了计算,而这个计算可以看做是将低维数据映射到了高维空间(自己的理解,就是一个隐式变换,我就认为计算后的高维数据。不知道这里理解的对不对?据说这样理解是有问题的,但是姑且这样理解吧。),最后求解这个分割面。
推荐一篇写的非常好的博客:很详细,由浅入深
http://blog.csdn.net/v_july_v/article/details/7624837