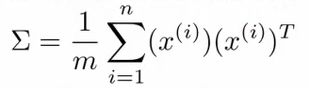吴恩达机器学习总结：第十一 降维（PCA）（大纲摘要及课后作业）

为了更好的学习，充分复习自己学习的知识，总结课内重要知识点，每次完成作业后都会更博。

英文非官方笔记

总结

1.动机I：数据压缩

（1）压缩

    a.加速算法

    b.减小数据空间

    c.2维降为1维例子

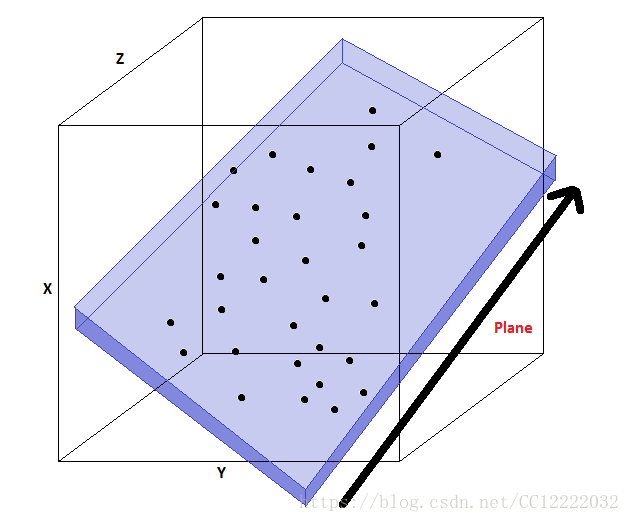
    d.3维降为2维例子

   

    e.在实际中，我们正常会将1000维将为100维

2.动机II:可视化

（1）很难可视化高维数据

    a.将为将会以易处理的方式来显示信息，以此提供给人进行处理

（2）我们关心降维的原因

    a.帮助理解数据，有助于开发算法

    b.降温帮助我们看到有用数据

    c.如果能在数据中展示，那么便可以很好地解释给别人

3.主成分分析（PCA）：问题表述

（1）从N维到K维

    a.找到k个向量(u(1), u(2), ... u(k)),使得投影误差最小

    b.可以使用k个向量定义平面上一个点

（2）PCA与线性回归对比

    a.PCA不是线性回归，尽管相似

    b.对于线性回归，拟合一条直线以最小化点与方形线之间的直线（点之间垂直距离）

    c.PCA是求正交化距离最短的

    d.线性回归需要预测y

4.PCA算法

（1）在进行数据压缩之前，需要对数据进行归一化处理（特征缩放和均值标准化）

（2）需要计算的两件事

    a.计算向量u

    b.计算向量z

（3）算法描述（从N维到K维）

    a.计算协方差矩阵（n x n）

    b.计算协方差矩阵的特征向量

        [U,S,V] = svd(sigma)

          

    c.取出u矩阵的前k列并堆积成列，我们记作Ureduce

    d.计算z，z = (Ureduce)T * x

（4）步骤

    a.压缩

    b.计算sigma

    c.用svd计算特征向量

    d.从U中去k个向量

    e.计算z（z = (Ureduce)T * x）

5.压缩表示法重建

6.选择主要组件的数量

（1）k是主要组件数量

（2）如何选择k

    a.最小化投影平方误差

    b.数据的总体变化可以定义为数据的平均值，表明来源的训练样本有多远

（3）可以这样

7.应用PCA的建议

（1）PCA将一个向量映射到较低维度向量

（2）通常，您可以将数据维度降低5-10倍，而不会对算法产生重大影响

8.PCA应用

（1）压缩

（2）可视化（选择k=2或者3）

（3）关于PCA，有不当使用

    a.使用PCA来防止过度拟合，这是不恰当的

    b.PCA丢失一些数据，但是不知道丢失的值是什么

（4）PCA第二个神话误区

    a.用来压缩数据和可视化很好

    b.最好在确定PCA会帮助你之后再添加PCA

作业

1.载入例程数据集

load ('ex7data1.mat'); plot(X(:, 1), X(:, 2), 'bo'); axis([0.5 6.5 2 8]); axis square;

2.主成分分析

[X_norm, mu, sigma] = featureNormalize(X); [U, S] = pca(X_norm); hold on; drawLine(mu, mu + 1.5 * S(1,1) * U(:,1)', '-k', 'LineWidth', 2); drawLine(mu, mu + 1.5 * S(2,2) * U(:,2)', '-k', 'LineWidth', 2); hold off; %featureNormalize函数 mu = mean(X); X_norm = bsxfun(@minus, X, mu); sigma = std(X_norm); X_norm = bsxfun(@rdivide, X_norm, sigma); end %pca函数 [m, n] = size(X); U = zeros(n); S = zeros(n); Sigma = 1/m * X'* X; [U, S, V] = svd(Sigma); end 

3.降维

plot(X_norm(:, 1), X_norm(:, 2), 'bo'); axis([-4 3 -4 3]); axis square K = 1; Z = projectData(X_norm, U, K); X_rec = recoverData(Z, U, K); hold on; plot(X_rec(:, 1), X_rec(:, 2), 'ro'); for i = 1:size(X_norm, 1) drawLine(X_norm(i,:), X_rec(i,:), '--k', 'LineWidth', 1); end hold off %projectData函数 Z = zeros(size(X, 1), K); U_reduce = U(:, 1:K); Z =X * U_reduce; end %recoverdata函数 X_rec = zeros(size(Z, 1), size(U, 1));       U_reduce = U(:, 1:K); X_rec = Z * U_reduce'; end 

4.载入可视化人脸数据

load ('ex7faces.mat') displayData(X(1:100, :));

5.PCA法应用人脸数据

[X_norm, mu, sigma] = featureNormalize(X); [U, S] = pca(X_norm); displayData(U(:, 1:36)');

6.人脸数据降维

K = 100; Z = projectData(X_norm, U, K);

7.降维之后可视化人脸

K = 100; X_rec = recoverData(Z, U, K); subplot(1, 2, 1); displayData(X_norm(1:100,:)); title('Original faces'); axis square; subplot(1, 2, 2); displayData(X_rec(1:100,:)); title('Recovered faces'); axis square;

8.进阶练习

A = double(imread('bird_small.png'));
A = A / 255;
img_size = size(A);
X = reshape(A, img_size(1) * img_size(2), 3);
K = 16; 
max_iters = 10;
initial_centroids = kMeansInitCentroids(X, K);
[centroids, idx] = runkMeans(X, initial_centroids, max_iters);
sel = floor(rand(1000, 1) * size(X, 1)) + 1;
palette = hsv(K);
colors = palette(idx(sel), :);
figure;
scatter3(X(sel, 1), X(sel, 2), X(sel, 3), 10, colors);
title('Pixel dataset plotted in 3D. Color shows centroid memberships');

[X_norm, mu, sigma] = featureNormalize(X);
[U, S] = pca(X_norm);
Z = projectData(X_norm, U, 2);
figure;
plotDataPoints(Z(sel, :), idx(sel), K);
title('Pixel dataset plotted in 2D, using PCA for dimensionality reduction');
fprintf('Program paused. Press enter to continue.\n');
pause;