路径规划之Field D*算法
提出背景:在以往的路径规划算法中,如A*, D*, D* Lite等, 机器人的运动角度被限制为π/4的倍数。因此我们也可以在相关的算法论文的实验部分看到一些我们觉得这样运动会造成成本变大的路径。基于此,field d*算法将取消运动角度为π/4的倍数这一限制,并且告诉机器人移动多大的角度。
思路分析:在网格地图的路径规划算法中,从某个结点(例如s)到目标结点的代价为:
![]() 其中nbrs(s)是s的所有相邻节点的集合;c(s, s’)是从s到s'的代价,g(s’)是节点s’到目标结点的代价。
其中nbrs(s)是s的所有相邻节点的集合;c(s, s’)是从s到s'的代价,g(s’)是节点s’到目标结点的代价。
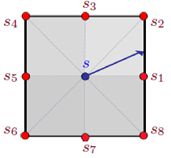
之前的算法都是假设从节点s到相邻节点的唯一可能的移动只能是直线轨迹(只能是从一格移动到另一格)。而Filed D*考虑放宽这个假设,允许从节点s到其网格单元边界上的任何一点的直线 轨迹(如图1蓝线所示)。那么相似的,我们只需要知道边s1s2上的sb的值,就可以通过最小化c(s, sb)+g(sb)来求得s点的代价。其中,c(s, sb) 的计算方式是s和sb之间的距离乘以到达s所在单元的代价。这里对s1,s2,,,s8的理解并不是一个网格的8个点,而是说他们分别代表了一个网格,把他们看成每个网格的质点即可。
图1 图2 图3
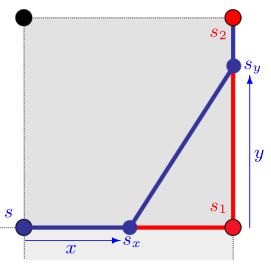
如图2所示,设s到s1的代价为b,s到s2的代价为c。再假设机器人按照图3的轨迹运动(可能的运动方式不止这一种,接下来会介绍)。那么 c(s,sy)=![]() .然后我们再通过线性插值法,令
.然后我们再通过线性插值法,令![]() .虽然这个假设并不完美,毕竟线性插值法是一种假设,但是实际应用中证明了这是行之有效的方法,因此这里姑且这样。至此,我们s点的路径代价可以计为:
.虽然这个假设并不完美,毕竟线性插值法是一种假设,但是实际应用中证明了这是行之有效的方法,因此这里姑且这样。至此,我们s点的路径代价可以计为:
现在我们接着上文讨论field d*算法有几种可能的运行路径。由于线性插值法,x和y中至少有一个为0或者1。如果能明确这一点,那么有几种运行路径就显而易见了。我们可以做一个简单的证明
首先令f=g(s1)-g(s2),把它看作是右边(right edge)即线段s1s2的代价大小。基于此,我们研究的问题等价于寻找一条从s到s2的最短路径。因为如果f<0,那么最短路径永远是从s到s1的那条底部水平线段,这相当于让f<0以便让机器人走过整个右边(举个例子,我们想从s1沿着右边运动到s2,所以问题就变成了寻找s到s1的最短路径)。当然这一部分只是从s到s2的路径成本,对于结点s的整个成本而言,还应该加上g(s2)。
现在,我们做出一个与上一段中红字相反的假设:x和y中没有一个为0或者1,机器人的运动路径如图4(a)的蓝线所示,它是最短路径,小于s到s1再到s2的路径成本。那么sx到sy的成本也就小于sx到s1再到sy,用公式表示为
图4
注意:这里切不可简单的理解为三角形的两边之和大于第三边,因为我们讨论的成本相当于图论中的边的权重,而不是边的长度。在图4(b)中作△(sx,s1,sy)的相似三角形,边的关系也同样满足。至此,观察图4(c),不难发现新的蓝色路径成本低于图4(a)的成本。得证。
因此,机器人的运行路径只有图(ii)(iii)(iv)所示的三种情况,分别对应{x=1,y=0},{x≠0,1 y=1},{x=0, y≠0,1}.那么这三种路径中哪个成本最低呢?这取决于c与b的相对大小以及f的值。
图 5
情形①:f<0,则g(s)=min(c,b)+g(s1).
情形②: f=b.那么图(iii)和(iv)的成本是一样的。我们可以通过求y(数值上等于1-x)的值得到最低成本路径。令k=f=b,则g(s)=![]() ,对y求导,令其为0,可求得取最小值时的y值为
,对y求导,令其为0,可求得取最小值时的y值为![]() .
.
情形③:f<b. 此时采用图5(iv)所示的路径,令k=f,用②中的式子计算成本
情形④: f>b. 此时采用图5(iii)所示的路径,令k=b,y=1-x,用②中的式子计算成本
P.S.:对于情形②中两个成本相等的说法,这里可以给出证明: