感知机算法原理（PLA原理）及 Python 实现

参考书籍：李航老师的《统计学习方法》、林轩田老师的《机器学习基石》

如无特殊说明，图片均来自网络(google图片、百度图片)，如有侵权请联系我，我会立即删除或更改

---

PLA 是 Perceptron Learning Algorithm 的缩写，也叫感知机算法。感知机算法与线性回归有很多相似的地方。例如线性回归采用梯度下降法求最优参数的时候对每个数据点都进行了遍历，求误差的平均值。而 PLA 只选取一个点进行处理，所以 PLA 的学习过程也可以叫做 随机梯度下降。

如果不了解什么是线性回归，可以参考我的另一篇文章：《机器学习笔记01：线性回归(Linear Regression)和梯度下降(Gradient Decent)》

---

1 感知机模型

1.1 形象的感知机

什么是感知机模型呢，简而言之就是可以将有两个特征的数据集中的正例和反例完全分开的关于一条直线的函数，或者可以是关于三维空间中的一个平面的函数，更可以是关于高维的一个超平面的函数。

什么？关于一条直线的函数？关于一个平面的函数？关于一个超平面的函数？其实感知机就是一个分段函数，不过变量是一条直线、平面或超平面而已。

可能听起来有点绕口，看了1.2节就明白了。当然如果数据集只有一个特征，那么也可以是一个点。比如下面的这条直线就将数据集中的正负实例完全分成了两部分：

或者下面的这个三维空间中的平面将有三个特征的数据集分成了两部分：

---

1.2 感知机的数学表示

上面的图片应该已经给了大家一个形象的理解：感知器就是一个东西能够把训练集中的正例和反例划分为两个部分，并且能够对未来输入的数据进行分类。举个例子：一个小孩子的妈妈在教他什么是苹果什么不是苹果，首先会拿个苹果过来说“记住，这个是苹果”，然后拿了一个杯子过来说“这个不是苹果”，又拿来一个稍微不一样的苹果说“这个也是苹果”……，最后，小孩子就学习到了一个模型（判断苹果的标准）来判断什么是苹果什么不是苹果。

首先，感知机的输入空间（特征空间）为 X⊆Rn ，即 n 维向量空间，输出空间为 Y={+1,−1} ，即 −1 代表反例， +1 代表正例。例如：输入 x∈X 对应于输入空间 Rn 中的某个点，而输出 y∈Y 表示该点所在的分类。需要注意的是，输入 x 是一个 n 维的向量，即 x=(x(1),x(2),...,x(n)) 。现在已经有了输入和输出的定义，我们就可以给出感知机 f(x) 的模型了：

f(x)=sign(ω⋅x+b)

其中，向量 ω=(ω(1),ω(2),...,ω(n)) 中的每个分量代表输入向量空间 Rn 中向量 x 的每个分量 xi 的权重，或者说参数。 b∈R 称为偏置单元， ω⋅x 表示 ω 和 x 的内积， sign 是一个符号函数，即：

sign(x)=⎧⎩⎨+1,−1,x⩾0x<0

我们把上面这个函数 f(x) 称为感知机。

---

1.3 感知机的假设空间

上面说了，感知机是一个模型，它具有输入和输出。但是我们事先并不知道这个模型到底是什么。同时我们也需要知道到哪里去寻找我们想要的感知机模型，所以这里有个概念叫做 假设空间，我们把假设空间用 H 表示，它是一个包含了在特征空间（输入空间） Rn 中定义的所有线性分类模型的一个集合，即有：

H={f|f(x)=sign(ω⋅x+b)}

李航老师《统计学习方法》中的假设空间没有 sign 函数，个人觉得既然是感知机模型的假设空间，而不是超平面（包括点、直线和平面）的集合，就应该将sign加上

而我们要希望得到就是一个最佳的（能够完美划分训练集的）感知机 hopt∈H 。例如下图中的各种直线就是二维假设空间 H 中的一部分模型去掉符号函数 sign 后的直线（不可能画出所有的直线），而直线 a 就是一个完美的划分直线（要注意模型和超平面的区别，即有无 sign 函数的区别）：

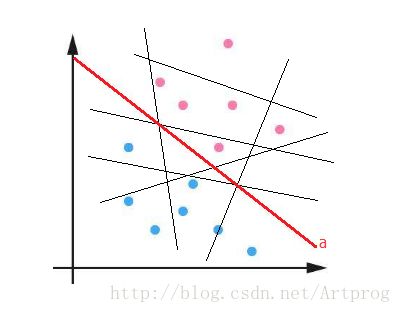
而其他直线（黑色）都不能把正例和反例完全分开。

---

1.4 感知机的几何意义

且先去掉感知机模型中用于输出分类结果的 sign 函数，如果我们有如下方程：

ω⋅x+b=0

那么这个方程的几何意义是什么呢？其意义很简单：

1. 方程 ω⋅x+b=0 是一个超平面的方程
2. ω 是这个超平面的法向量
3. b 是这个超平面的截距

例如在三维空间坐标系内，平面的方程均可用三元一次方程 Ax+By+Cz+D=0 来表示，其中 ω=(A,B,C) ， x=(x,y,z) ， d=D 。很明显，如下图所示，这个三维空间中的平面把整个三维空间分成了两个部分。对于更高维度的平面我们可能想象不出来，但是它们的性质却是相同的。

---

1.5 感知机的输入和输出

总结一下目前用到的符号，我们需要知道以下数学符号的含义：

符号	含义
H	假设空间
f(x)∈H	感知机模型
X⊆Rn	特征空间
Y={+1,−1}	输出空间
Rn	n 维向量空间
ω=(ω(1),ω(2),...,ω(n))	超平面的法向量，或者说特征的参数向量
ω(i),(i=1,2,...,n)	超平面的法向量的分量，或者说某个参数
x=(x(1),x(2),...,x(n))	输入向量，特征向量
x(i),(i=1,2,...,n)	特征向量中的某个特征
b	超平面的截距
sign(x)	符号函数, x⩾0 时为 +1 ，否则为 −1
D=(x1,y1),(x2,y2),...,(xm,ym)	数据集， m 为样本数, n 为特征数， y 为分类标签（1或者-1）

注意

D=x1,x2,...,xm=⎛⎝⎜⎜⎜⎜⎜⎜x(1)1x(1)2⋮x(1)mx(2)1x(2)2⋮x(2)m⋯⋯⋱⋯x(n)1x(n)2⋮x(n)my1y2⋮ym⎞⎠⎟⎟⎟⎟⎟⎟

以上某些符号在后面会用到。

---

2. 感知机的学习过程

2.1 数据集的线性可分和线性不可分

感知机要求训练数据是线性可分的，否则无法构建一个线性的分类器。什么是线性可分和线性不可分呢，直观的表示如下：

除了第一个数据集是线性可分的，其他两个都不是线性可分的。上图是二维空间中的情况，高维空间的情况也一样。

下面是数据集线性可分的定义（李航《统计学习方法》P26）：

给定一个数据集

D=(x1,y1),(x2,y2),...,(xn,yn)

其中， xi∈X⊆Rn ， yi∈Y={+1,−1} ， i=1,2,..,n 。如果存在某个超平面 S

ω⋅x+b=0

能够将数据集的正实例点和负实例点完全正确地划分到超平面的两侧，即对所有 yi=+1 的实例 i ，有 ω⋅xI+b>0 ，对所有 yi=−1 的实例 i ，有 ω⋅xI+b<0 ，则数据集 D 为线性可分数据集（linearly separable data set）；否则，称数据 D 集线性不可分

---

2.2 PLA 原理及过程

PLA 的原理很简单，开始时，我们令 ω=b=0 ，然后在训练数据 D 中任意选择一点，如果该点被错误分类了，那么我们就调整分类的直线或者超平面使该点能够被正确分类。

在说明 PLA 原理之前，我们先来回顾一下向量的内积（inner product）。例如有向量 a=(a(1),a(2),...,a(n)),b=(b(1),b(2),...,b(n)) ，则它们的内积为：

a⋅b=∑i=1na(i)b(i)=∥a∥⋅∥b∥⋅cosθ

在纸上画画就明白，当内积为负数时，两个向量的夹角 θ 大于 90° ；当内积为正数时，两个向量的夹角 θ 小于 90° ；当内积为 0 时，两个向量垂直。

在 1.4 节我们给出了感知机的几何意义，方程 ω⋅x+b=0 代表了一个平面。我们不妨将其改写为 ω^⋅x^=0 ，其中：
ω^=(b,ω)=(ω0,ω)=(ω(0),ω(1),ω(2),...,ω(n))
x^=(1,x)=(1,x(1),x(2),...,x(n))
我们的目的就是求得超平面的法向量 ω^ ， 使超平面能够完美地划分数据集。

具体怎么求呢，我们采用随机梯度下降法，即随意找一个点，如果分类错误，我们就更新 ω^ ：

1. 输入数据 D=(x1,y1),(x2,y2),...,(xm,ym) ，其中 xi∈X⊂Rn ， y∈Y={+1,−1} ， i=1,2,...,n 。
2. 选取初值 ω^0=0 ，即设为零向量。
3. 遍历 D 中的数据，如果遇到某个样本 (xi,yi) 使得 yi(ω^⋅x)⩽0 ，即目前分类输出和真实分类不同，则
   ω^←ω^0+yix^i
4. ω^ 更新后，回到第三步，重新开始遍历，如果遍历完整个数据集 D 都未有更新操作（没有错误分类点），则转第五步。
5. 输出当前超平面的法向量 ω^ 。

最后程序输出的 ω^ 即为我们要找的能够完美划分数据集的超平面的法向量。

下面来看一个例子（出自林轩田老师的《机器学习基石》），红色代表当前超平面的法向量，紫色代表本次更新后的法向量，黑色代表随机选择的一个错误的分类点，注意是如何调整超平面的：

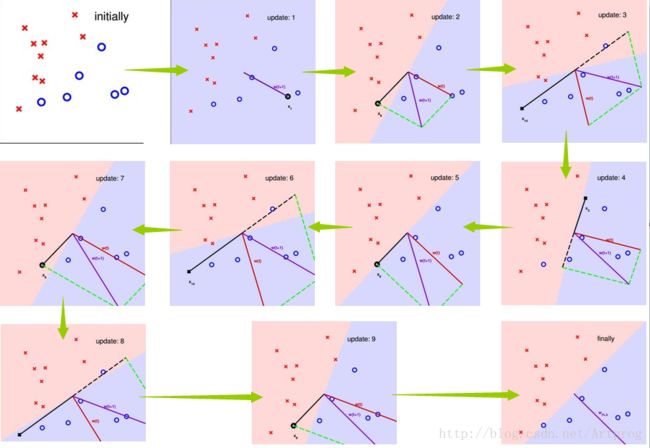
最后看起来好像还有一个蓝色的点在超平面上，其实放大后发现，这个点的圆心是在正例一方的。所以感知机训练完成。

---

2.3 PLA 的收敛性证明

可能很多朋友会怀疑上面的算法最终会不会停止，因为每更新一次 ω^ ，可能就会有新的错误分类点出现。先说结论吧，对于线性可分的数据集，PLA 最终是会停止的，即满足算法的有穷性，并且误分类的次数也是有上界的。

李航老师《统计学习方法》P33页中的证明可能会让很多人摸不着头脑，为啥 ∥ω^opt∥=1 呢，为什么不可以是其他的值呢？答案是： ∥ω^opt∥ 可以取任何正实数。

下面就来证明一下 PLA 的收敛性（参考李航《统计学习方法》、林轩田《机器学习基石》、MIT机器学习PPT）：

设存在理想超平面 S 能够完全正确划分数据集 D ，其法向量（模型参数向量）为 ω^opt 。

令 γ=min0⩽i⩽myi(ω^⋅x^i) ，即 γ 为离超平面最近的数据点与超平面的距离（ m 为样本数量，后文中的含义相同）。那么，对于任意的点 x^i 均有

yi(ω^⋅x^i)⩾γ

令感知机算法从 ω^0 =0 开始，每遇到错误分类就更新参数向量，令 ω^k−1 为遇到第 k 个错误分类之前的参数向量，则遇到第 k 个误分类情况时需要满足

yi(ω^k−1⋅x^i)⩽0

若 (x^i,yi) 是被 ω^k−1 错误分类的数据，则更新参数向量：

ω^k=ω^k−1+yix^i

下面证明两个不等式用于后面的证明：
（1） ω^k⋅ω^opt⩾kγ ：

ω^k⋅ω^opt=ω^k−1⋅^ωopt+yix^iω^opt⩾ω^k−1⋅ωopt+γ

又：

ω^k−1⋅ω^opt=ω^k−2⋅^ωopt+yix^iω^opt⩾ω^k−2⋅ωopt+γ

所以可以得到如下递推公式：

ω^k⋅ω^opt⩾ω^k−1⋅ωopt+γ⩾ω^k−2⋅ωopt+2γ⩾...⩾ω^1⋅ωopt+(k−1)γ⩾ω^0⋅ωopt+kγ=kγ

---

（2） ∥ω^k∥2⩽kR2 ：

∥ω^k∥2=∥ω^k−1∥2+2yiω^k−1⋅x^i+y2i∥x^i∥2,(yi∈{+1,−1}，可略去y2i)

因为处理都是错误分类，所以 yiω^k−1⋅x^i⩽0
所以：

∥ω^k∥2⩽∥ω^k−1∥2+∥x^i∥2

令 R=max0⩽i⩽m∥x^i∥ ，即离原点最远的点与原点的距离。则：

∥ω^k∥2⩽∥ω^k−1∥2+R2

又：

∥ω^k−1∥2⩽∥ω^k−2∥2+R2

所以有递推公式：

∥ω^k∥2⩽∥ω^k−1∥2+R2⩽∥ω^k−2∥2+2R2⩽...⩽∥ω^1∥2+(k−1)R2⩽∥ω^0∥2+kR2⩽kR2

所以，由（1）、（2）可知：

1⩾cosθ=ω^k⋅ω^opt∥ω^k∥∥ω^opt∥⩾kγ∥ω^k∥∥ω^opt∥⩾kγkR2−−−√∥ω^opt∥

其中 θ 为 ω^k 和 ω^opt 的夹角。
所以由上面的不等式可知：

k⩽R2∥ω^opt∥2γ2

所以，感知机的错误修正次数是有上限的，由于 ∥ω^opt∥ 是必然存在的，所以 k 一定存在。即感知机算法是收敛的。

---

3. 用 Python 实现感知机

由于篇幅太大，实现另开一篇：感知机的 python 实现

如有错误，请批评指正

---

最近遇到很多转载不注明出处，还打着原创旗号的小编和博主，所以：

本文采用 知识共享署名-非商业性使用-禁止演绎 2.5 中国大陆许可协议 进行许可。

---