LeetCode刷题日记（Day 2）— Array

LeetCode 299. Bulls and Cows

string getHint(string secret, string guess) {
    int a = 0, b = 0, counter[11] = {0};
    for(int i = 0; i < secret.size(); i++)
        counter[secret[i]-'0']++;

    for(int i = 0; i < secret.size(); i++)
        if(secret[i] == guess[i]) {
            counter[secret[i]-'0']--;
            guess[i] = char('9'+1);
            a++;
        }

    for(int i = 0; i < guess.size(); i++)
        if(counter[guess[i]-'0'] > 0) {
            counter[guess[i]-'0']--;
            b++;
        }

    return to_string(a) + "A" + to_string(b) + "B";
}

思路：多次循环检查，首先计算a值，后使用 guess[i] = char('9'+1) 的方式排除之后对b值检查的干扰，b值使用counter计数的方法计算。

注意点：C++ 中 string 的 to_string() 方法是 C++11 中才有的，命令行编译需添加 -std=c++11

 

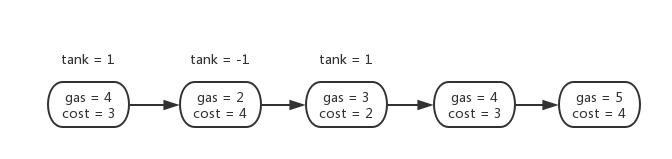
LeetCode 134. Gas Station

int canCompleteCircuit(vector& gas, vector& cost) {
    int tol_gas = 0, tol_cost = 0, cur = 0, index = 0;
    for(int i = 0; i < gas.size(); i++)
        tol_gas += gas[i];
    
    for(int i = 0; i < cost.size(); i++)
        tol_cost += cost[i];
    
    if(tol_cost > tol_gas) return -1;
    
    for(int i = 0; i < gas.size(); i++) {
        cur += gas[i];
        cur -= cost[i];
        if(cur < 0) {
            cur = 0;
            index = i+1;
        }
    }
    
    return index;
}

思路：我们可以证明若所有的gas数量加起来比cost数量多，则一定有解。之后我们逐个遍历，当在某个站点，油箱剩余为负数时，说明之前所有站点都不是可行的起始点（证明在之后给出），因此直接跳到下一个站点继续之前的步骤。

证明：为什么油箱剩余为负数时，之前的站点不是可行的起始点？

我们举个例子，在经过1站点后，出现油箱为负数的情况，因此从0站点开始是不可行的，为什么不可以从1站点开始的原因是，要到达1站点的条件是经过0站点后油箱不能为负，即从1站点开始的话，油箱剩余会越少（更小的负数）。

 

LeetCode 118. Pascal's Triangle

vector > generate(int numRows) {
    vector > res;
    for(int i = 0; i < numRows; i++) {
        vector vec(i+1, 1);
        for(int j = 1; j < i; j++)
            vec[j] = res[i-1][j-1] + res[i-1][j];
        res.push_back(vec);
    }
    return res;
}

思路：无，按照规律逐层计算即可

 

LeetCode 119. Pascal's Triangle II

vector getRow(int rowIndex) {
    vector res(rowIndex+1, 1);
    for(int i = 2; i <= rowIndex; i++)
        for(int j = i-1; j > 0; j--)
            res[j] = res[j] + res[j-1];
    return res;
}

思路：按规律计算，注意要从后往前计算。

 

LeetCode 169. Majority Element

int majorityElement(vector& nums) {
    int n = nums.size();
    unordered_map counter;
    for(int i = 0; i < nums.size(); i++)
        if(++counter[nums[i]] > n/2)
            return nums[i];
    return 0;
}

思路：题目原意为找一个数量大于n/2的数，也就是找出数组中的众数（反之不成立）。我采用的是计数的方法，用 C++11的 unordered_map 可以明显提高速度。

除此之外，jianchao-li 的评论中提出六种有趣的解决方案，我选出其中几种讲解一下：

1. Hash Table 即我使用的方法，参见题解。

2. 排序法：我们可以直观知道，这个数排序后必然在n/2的位置上，考虑两种极端的情况：（1）这个数是最小的，由于它的数量超过n/2，因此排序后自然n/2个数就是要找的数，（2）这个数是最大的情况相同。jianchao-li使用了STL中的 nth-element() 函数（使用方法：nth_element(start, start+n, end) 方法可以使第n大元素处于第n位置（从0开始,其位置是下标为 n的元素），并且比这个元素小的元素都排在这个元素之前，比这个元素大的元素都排在这个元素之后，但不能保证他们是有序的）

int majorityElement(vector& nums) {
    nth_element(nums.begin(), nums.begin() + nums.size() / 2, nums.end());
    return nums[nums.size() / 2];
} 

3. 随机法：这个初看有点随缘，但是作者测试后的效果还是不错的，大概是因为有n/2个数的原因吧2333

int majorityElement(vector& nums) {
    int n = nums.size();
    srand(unsigned(time(NULL)));
    while (true) {
        int idx = rand() % n;
        int candidate = nums[idx];
        int counts = 0; 
        for (int i = 0; i < n; i++)
            if (nums[i] == candidate)
                counts++; 
        if (counts > n / 2) return candidate;
    }
}

4. 摩尔投票法：为什么感觉有点现实主义了2333，思路是“人多力量大”，首先选择一个数作为major，遍历，若与major相同则支持（count++），否则反对（count--），显然最终的 major 是数量超过n/2的那个数。

int majorityElement(vector& nums) {
    int major, counts = 0, n = nums.size();
    for (int i = 0; i < n; i++) {
        if (!counts) {
            major = nums[i];
            counts = 1;
        }
        else counts += (nums[i] == major) ? 1 : -1;
    }
    return major;
}

投票法的另一种理解：每次去除两个不相同的数字，最后留下的即为所找目标。

 

LeetCode 229. Majority Element II

vector majorityElement(vector& nums) {
    int n = nums.size();
    vector res;
    unordered_map m;
    for(int i = 0; i < n; i++)
        m[nums[i]]++;
    for(auto iter = m.begin(); iter != m.end(); ++iter) 
        if(iter->second > n/3)
            res.push_back(iter->first);
    return res;
}

思路：计数，统计数量超过 n/3 的数

讨论区的 oterman 提出升级版的摩尔投票法：不是吹，这年头很少有我这么写注释的了 ，非常的有意思。