【超参数寻优】交叉验证(Cross Validation)超参数寻优的python实现:单一参数寻优
【超参数寻优】交叉验证(Cross Validation)超参数寻优的python实现:单一参数寻优
- 一、交叉验证的意义
- 二、常用的交叉验证方法
- 1、Hold one method
- 2、K-flod CV
- 3、Leave-One-Out CV(LOO-CV)
- 二、交叉验证参数寻优的python实现
- 1、训练模型和待寻优参数
- 2、算法执行步骤
- 3、交叉验证参数寻优的python实现
- 4、参数C与评价指标的关系
- 参考资料
有关交叉验证的博文有很多,这里我会引用几篇博文【参考资料1,2,3,4】,帮助大家温习一下。交叉验证可以用于机器学习训练模型的性能评价,也可以进行参数寻优,本博文主要介绍交叉验证用于机器学习参数寻优的方法。
一、交叉验证的意义
交叉验证将原始数据集分组,一部分作为训练集,一本分作为验证集。训练集用于训练模型,验证集用于评价训练模型的性能指标。
参数寻优的意义:参数的数值决定着模型的性能。
交叉验证进行参数寻优的意义:如果训练和验证的数据集是相同的,可能验证的结果特别好,但是对于新的数据集预测效果就差强人意,因为过拟合(over-fitting)。采用交叉验证方法可以保障验证数据集没有参与过模型的训练,可以给出较为准确的参数寻优结果。
二、常用的交叉验证方法
1、Hold one method
样本数据被分为两组,一组作为训练数据集,用于训练模型,另一组作为验证数据集,用于评估模型性能。
优点:容易实现,处理简单。
缺点:没有用到交叉的方法,验证数据集对于模型的训练没有任何贡献。
2、K-flod CV
样本数据被分为 k k k组,每次将一组作为验证数据集,其余的 k − 1 k-1 k−1组作为训练数据集。这样就会有 k k k个训练模型,这 k k k个模型的验证准确率的平均值作为模型的性能指标。
优点:所有的样本都会被用于模型训练,评价结果可信。
缺点:相较于Hold one method,处理较为复杂。
3、Leave-One-Out CV(LOO-CV)
设原始数据集中有 K K K个样本,每次选择一个样本作为验证数据集,其余的 K − 1 K-1 K−1个样本作为训练数据集,这样就会有 K K K个训练模型,这 K K K个训练模型的验证准确率平均值为模型的性能指标。
优点:每次模型训练,几乎所有的样本都会应用到,结果最可信。
缺点:需要训练的模型较多,且训练数据集样本大,计算成本高。
二、交叉验证参数寻优的python实现
1、训练模型和待寻优参数
本博文选用的训练模型为线性的SVM模型(参考资料【5】),模型的数学表达为:
min W , b 1 2 ∥ W ∥ 2 + C 2 ∑ i = 1 m e i 2 s . t . y i ( W ⋅ x i + b ) ≥ 1 − e i , i = 1 , ⋯ , m e i ≥ 0 , i = 1 , ⋯ , m \begin{array}{l} \mathop {\min }\limits_{W,b} \frac{1}{2}{\left\| W \right\|^2} + \frac{C}{2}\sum\limits_{i = 1}^m {e_i^2} \\ s.t.{y_i}\left( {W \cdot {x_i} + b} \right) \ge 1 - {e_i},i = 1, \cdots ,m\\ {e_i} \ge 0,i = 1, \cdots ,m \end{array} W,bmin21∥W∥2+2Ci=1∑mei2s.t.yi(W⋅xi+b)≥1−ei,i=1,⋯,mei≥0,i=1,⋯,m
其中 W W W和 b b b是分隔超平面的权重和偏置,模型的训练就是为了训练 W W W和 b b b的值。 C C C是正则化参数,对模型的性能有很大的影响,本博文就是用3-flod交叉验证方法求参数 C C C值。
2、算法执行步骤
步骤一、设置参数 C C C的取值范围
步骤二、从第一个取值开始,将原始数据集分为3个子数据集(3-flod CV),每次将两个数据子集作为训练集用于线性SVM模型的训练,一个数据子集用于模型验证,共训练3个模型,取三个模型的验证准确率的平均值作为评价指标。参数 C C C的取值指针加1,重复步骤二,直到最后一个参数 C C C的取值。
步骤三:画出参数 C C C与对应评价指标的示意图。
3、交叉验证参数寻优的python实现
代码及样本地址 https://github.com/shiluqiang/CV_parameter_optimization
import numpy as np
from sklearn import svm
from sklearn import cross_validation
import matplotlib.pyplot as plt
def load_data(file_name):
'''导入数据集和标签
input:file_name(string):存储数据的地址
output:trainX(array):样本数据集
trainY(array):样本标签
'''
f = open(file_name)
trainX = []
trainY = []
for line in f.readlines():
X_tmp = []
Y_tmp = []
lines = line.strip().split('\t')
for i in range(len(lines)-1):
X_tmp.append(float(lines[i]))
Y_tmp.append(float(lines[-1]))
trainX.append(X_tmp)
trainY.append(Y_tmp)
f.close()
return np.array(trainX),np.array(trainY)
###1.导入训练样本和标签
trainX,trainY = load_data('data.txt')
trainY = trainY[:,0]
###2.设置C的取值范围
c_list = []
for i in range(1,21):
c_list.append(i * 0.5)
###3.交叉验证优化参数C
cv_scores = []
for j in c_list:
linear_svm = svm.SVC( kernel = 'linear', C = j)
scores = cross_validation.cross_val_score(linear_svm,trainX,trainY,cv =3,scoring = 'accuracy')
cv_scores.append(scores.mean())
fig = plt.figure().add_subplot(111)
fig.plot(c_list,cv_scores)
fig.set_xlabel('C')
fig.set_ylabel('Average accuracy')
plt.show()
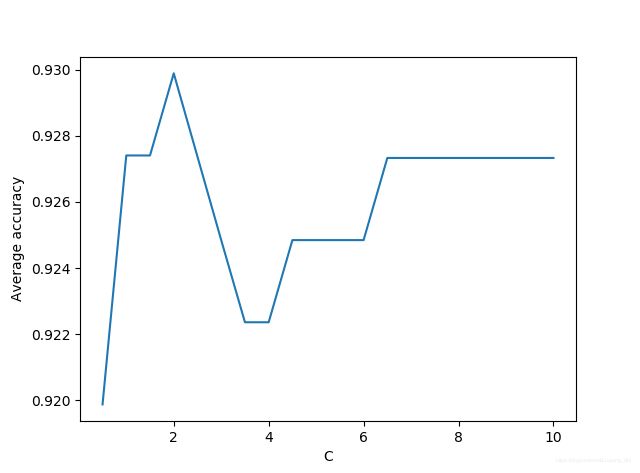
4、参数C与评价指标的关系
参考资料
1.https://blog.csdn.net/yawei_liu1688/article/details/79138202
2 https://blog.csdn.net/wong2016/article/details/81407927
3. http://www.cnblogs.com/pinard/p/5992719.html
4. https://blog.csdn.net/qq_36523839/article/details/80707678
5. https://blog.csdn.net/google19890102/article/details/35566949