【机器学习】概率神经网络（PNN）的python实现

一、概率神经网络原理

概率神经网络（Probabilistic Neural Network）的网络结构类似于RBF神经网络，但不同的是，PNN是一个前向传播的网络，不需要反向传播优化参数。这是因为PNN结合了贝叶斯决策，来判断测试样本的类别。

1.1、贝叶斯决策

假设对于测试样本$x$，共有$m$中类别可能$\{w_1,\cdots ,w_m\}$，则判断样本类别的贝叶斯决策是:

$\max \{p(w_1|x),p(w_2|x),\cdots ,p(w_m|x)\}$

1.2、PNN的网络结构

要介绍上述概率密度$p(w_i|x)$如何计算，首先要介绍PNN的网络结构。

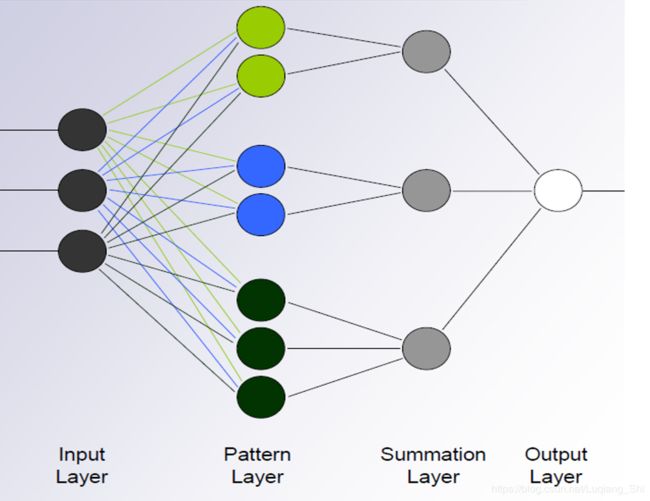
本博文的PNN结构图参考资料【2】，图中样本特征维度为3，由上图可知，PNN的网络结构分为四层：输入层，模式层、求和层、输出层。假设训练样本为$\left\{tr{x}_1,tr{x}_2,\cdots ,tr{x}_l\right\}$，其中样本个数为$l$。PNN各层的作用于相互之间关系描述如下：
输入层：输入测试样本，节点个数等于样本的特征维度。
模式层：计算测试样本与训练样本中的每一个样本的Gauss函数的取值，节点个数等于训练样本的个数。
测试样本$x$与第$j$个训练样本$tr{x}_j$之间的Gauss函数取值（对于测试样本$x$，从第$j$个模式层节点输出的数值）为：
$Gauss(x-tr{x}_j)=e^{-\frac{\Vert x-tr{x}_j\Vert }{2{\delta }^2}}$
其中$\delta$是模型的超参数（机器学习模型中，超参数是在开始学习过程之前设置值的参数），需要提前设定，也可以通过寻优算法（GA，QGA，PSO，QPSO等）获得。
求和层：求取相同类别测试样本对应的模式层节点输出之和，节点个数等于训练样本的类别个数。
输出层：对上述求和层输出进行归一化处理求取测试样本对应不同类别的概率，根据概率大小判断测试样本的类别，节点个数为1。

二、概率神经网路的优点与不足

2.1、优点（参考资料【1】）

收敛快：没有模型参数需要训练，收敛速度快。
非线性逼近：可以实现任意的非线性逼近，用PNN网络形成的判决曲面与贝叶斯最优准则下的曲面非常接近。
容错性高：模型层采用径向基函数（Gauss函数），考虑了不同类别样本之间的相互影响，对异常数据不敏感。

2.2、缺点

计算复杂度高：每个测试样本要与全部的训练样本进行计算。
空间复杂度高：因为没有模型参数，对于测试样本全部的训练样本都要参与计算，因此需要存储全部的训练样本。

三、PNN的python实现

完整python代码与样本地址：https://github.com/shiluqiang/PNN_python
本博文采用的数据集有两个类别，用全部的数据集作为训练集，数据集中的一半作为测试集，Gauss函数中的$\delta$设为0.1。
首先，对测试集和训练集进行归一化处理。

def Normalization(data):
    '''样本数据归一化
    input:data(mat):样本特征矩阵
    output:Nor_feature(mat):归一化的样本特征矩阵
    '''
    m,n = np.shape(data)
    Nor_feature = copy.deepcopy(data) 
    sample_sum = np.sqrt(np.sum(np.square(data),axis = 1))   
    for i in range(n):
        Nor_feature[:,i] = Nor_feature[:,i] / sample_sum        
    return Nor_feature

然后，计算测试集样本与训练集样本的欧氏距离。

def distance(X,Y):
    '''计算两个样本之间的距离
    '''
    return np.sqrt(np.sum(np.square(X-Y),axis = 1))
def distance_mat(Nor_trainX,Nor_testX):
    '''计算待测试样本与所有训练样本的欧式距离
    input:Nor_trainX(mat):归一化的训练样本
          Nor_testX(mat):归一化的测试样本
    output:Euclidean_D(mat):测试样本与训练样本的距离矩阵
    '''
    m,n = np.shape(Nor_trainX)
    p = np.shape(Nor_testX)[0]
    Euclidean_D = np.mat(np.zeros((p,m)))
    for i in range(p):
        for j in range(m):
            Euclidean_D[i,j] = distance(Nor_testX[i,:],Nor_trainX[j,:])[0,0]
    return Euclidean_D

其次，计算上述距离矩阵对应的Gauss函数值矩阵。

def Gauss(Euclidean_D,sigma):
    '''测试样本与训练样本的距离矩阵对应的Gauss矩阵
    input:Euclidean_D(mat):测试样本与训练样本的距离矩阵
          sigma(float):Gauss函数的标准差
    output:Gauss(mat):Gauss矩阵
    '''
    m,n = np.shape(Euclidean_D)
    Gauss = np.mat(np.zeros((m,n)))
    for i in range(m):
        for j in range(n):
            Gauss[i,j] = math.exp(- Euclidean_D[i,j] / (2 * (sigma ** 2)))
    return Gauss

再次，计算每个测试样本对应于每个类别概率和训练样本的类别种类。

def Prob_mat(Gauss_mat,labelX):
    '''测试样本属于各类的概率和矩阵
    input:Gauss_mat(mat):Gauss矩阵
          labelX(list):训练样本的标签矩阵
    output:Prob_mat(mat):测试样本属于各类的概率矩阵
           label_class(list):类别种类列表
    '''
    ## 找出所有的标签类别
    label_class = []
    for i in range(len(labelX)):
        if labelX[i] not in label_class:
            label_class.append(labelX[i])
    
    n_class = len(label_class)
    ## 求概率和矩阵
    p,m = np.shape(Gauss_mat)
    Prob = np.mat(np.zeros((p,n_class)))
    for i in range(p):
        for j in range(m):
            for s in range(n_class):
                if labelX[j] == label_class[s]:
                    Prob[i,s] += Gauss_mat[i,j]
    Prob_mat = copy.deepcopy(Prob)
    Prob_mat = Prob_mat / np.sum(Prob,axis = 1)
    return Prob_mat,label_class

最后，根据测试样本对应于每个类别概率和训练样本的类别种类求出测试样本对应的类别。

def calss_results(Prob,label_class):
    '''分类结果
    input:Prob(mat):测试样本属于各类的概率矩阵
          label_class(list):类别种类列表
    output:results(list):测试样本分类结果
    '''
    arg_prob = np.argmax(Prob,axis = 1) ##类别指针
    results = []
    for i in range(len(arg_prob)):
        results.append(label_class[arg_prob[i,0]])
    return results

参考资料

1、https://blog.csdn.net/guoyunlei/article/details/76209647
2、https://wenku.baidu.com/view/bb2f52c64128915f804d2b160b4e767f5acf804b.html