《算法图解》学习笔记(八):贪婪算法和NP完全问题(附代码)
python学习之路 - 从入门到精通到大师
文章目录
- [python学习之路 - 从入门到精通到大师](https://blog.csdn.net/TeFuirnever/article/details/90017382)
- 一、教室调度问题
- 二、背包问题
- 三、集合覆盖问题
- 四、近似算法
- 1)准备工作
- 2)计算答案
- 3)集合
- 4)回到代码
- 五、NP 完全问题
- 1)旅行商问题详解
- 1。3个城市
- 2。4个城市
- 2)如何识别 NP 完全问题
- 六、总结
- 参考文章
一、教室调度问题
假设有如下课程表,你希望将尽可能多的课程安排在某间教室上。

你没法让这些课都在这间教室上,因为有些课的上课时间有冲突。
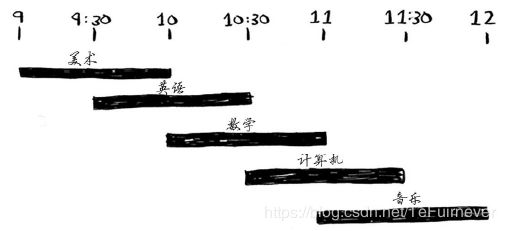
你希望在这间教室上尽可能多的课。如何选出尽可能多且时间不冲突的课程呢?这个问题好像很难,不是吗?实际上,算法可能简单得让你大吃一惊。具体做法如下:
- 选出结束最早的课,它就是要在这间教室上的第一堂课。
- 接下来,必须选择第一堂课结束后才开始的课。同样,你还是选择结束最早的课,这将是要在这间教室上的第二堂课。
重复这样做就能找出答案!下面来试一试。美术课的结束时间最早,为10:00 a.m.,因此它就是第一堂课。
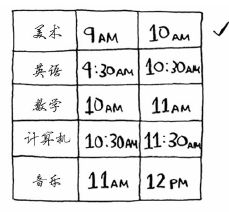
接下来的课必须在10:00 a.m.后开始,且结束得最早。

英语课不行,因为它的时间与美术课冲突,但数学课满足条件。最后,计算机课与数学课的时间是冲突的,但音乐课可以。

因此将在这间教室上如下三堂课。

很多人都跟我说,这个算法太容易、太显而易见,肯定不对。但这正是贪婪算法的优点——简单易行!贪婪算法很简单:每步都采取最优的做法。在这个示例中,你每次都选择结束最早的课。用专业术语说,就是你每步都选择局部最优解,最终得到的就是全局最优解。信不信由你,对于这个调度问题,上述简单算法找到的就是最优解!
显然,贪婪算法并非在任何情况下都行之有效,但它易于实现!
二、背包问题
来看一个例子,假设你是个贪婪的小偷,背着可装35磅(1磅 ≈ 0.45千克)重东西的背包,在商场伺机盗窃各种可装入背包的商品。你力图往背包中装入价值最高的商品,你会使用哪种算法呢?

同样,你采取贪婪策略,这非常简单。
- 盗窃可装入背包的最贵商品。
- 再盗窃还可装入背包的最贵商品,以此类推。
只是这次这种贪婪策略不好使了!例如,你可盗窃的商品有下面三种。

你的背包可装35磅的东西。音响最贵,你把它给偷了,但背包没有空间装其他东西了。
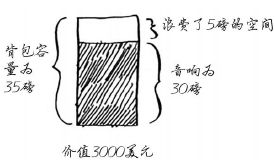
你偷到了价值3000美元的东西。且慢!如果不是偷音响,而是偷笔记本电脑和吉他,总价将为3500美元!

在这里,贪婪策略显然不能获得最优解,但非常接近。不过小偷去购物中心行窃时,不会强求所偷东西的总价最高,只要差不多就行了。
从这个示例你得到了如下启示:在有些情况下,完美是优秀的敌人。有时候,你只需找到一个能够大致解决问题的算法,此时贪婪算法正好可派上用场,因为它们实现起来很容易,得到的结果又与正确结果相当接近。
三、集合覆盖问题
假设你办了个广播节目,要让全美50个州的听众都收听得到。为此,你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用,因此你力图在尽可能少的广播台播出。现有广播台名单如下:

每个广播台都覆盖特定的区域,不同广播台的覆盖区域可能重叠。
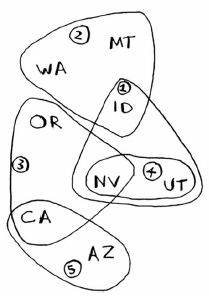
如何找出覆盖全美50个州的最小广播台集合呢?听起来很容易,但其实非常难。具体方法如下。
- 列出每个可能的广播台集合,这被称为 幂集(power set)。可能的子集有 2 n 2^n 2n个。
- 在这些集合中,选出覆盖全美50个州的最小集合。
问题是计算每个可能的广播台子集需要很长时间。由于可能的集合有 2 n 2^n 2n个,因此运行时间为O( 2 n 2^n 2n)。如果广播台不多,只有5~10个,这是可行的。但如果广播台很多,结果将如何呢?随着广播台的增多,需要的时间将激增。假设你每秒可计算10个子集,所需的时间将如下。

没有任何算法可以足够快地解决这个问题!怎么办呢?
四、近似算法
贪婪算法可化解危机!使用下面的贪婪算法可得到非常接近的解。
- 选出这样一个广播台,即它覆盖了最多的未覆盖州。即便这个广播台覆盖了一些已覆盖的州,也没有关系。
- 重复第一步,直到覆盖了所有的州。
这是一种 近似算法(approximation algorithm)。在获得精确解需要的时间太长时,可使用近似算法。判断近似算法优劣的标准如下:
- 速度有多快;
- 得到的近似解与最优解的接近程度。
贪婪算法是不错的选择,它们不仅简单,而且通常运行速度很快。在这个例子中,贪婪算法的运行时间为O( n 2 n^2 n2),其中n为广播台数量。
下面来看看解决这个问题的代码。
1)准备工作
出于简化考虑,这里假设要覆盖的州没有那么多,广播台也没有那么多。
首先,创建一个列表,其中包含要覆盖的州。
states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"]) # 传入一个数组,它被转换为集合
使用集合来表示要覆盖的州。集合类似于列表,只是同样的元素只能出现一次,即 集合不能包含重复的元素。例如,假设有如下列表。
>>> arr = [1, 2, 2, 3, 3, 3]
并且将其转换为集合。
>>> set(arr)
set([1, 2, 3])
在这个集合中,1、2和3都只出现一次。

还需要有可供选择的广播台清单,选择使用哈希表来表示它。
stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])
其中的键为广播台的名称,值为广播台覆盖的州。在该示例中,广播台kone覆盖了爱达荷州、内达华州和犹他州。所有的值都是集合。马上你就会看到,使用集合来表示一切可以简化工作。
最后,需要使用一个集合来存储最终选择的广播台。
final_stations = set()
2)计算答案
接下来需要计算要使用哪些广播台。根据下边的示意图,你能确定应使用哪些广播台吗?
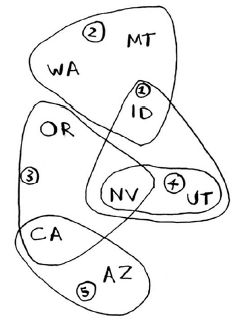
正确的解可能有多个。需要遍历所有的广播台,从中选择覆盖了最多的未覆盖州的广播台。然后将这个广播台存储在best_station中。
best_station = None
states_covered = set()
for station, states_for_station in stations.items():
states_covered 是一个集合,包含该广播台覆盖的所有未覆盖的州。for 循环迭代每个广播台,并确定它是否是最佳的广播台。下面来看看这个 for 循环的循环体。
covered = states_needed & states_for_station # 计算交集
if len(covered) > len(states_covered):
best_station = station
states_covered = covered
其中有一行代码看起来很有趣。
covered = states_needed & states_for_station
3)集合
假设你有一个水果集合。
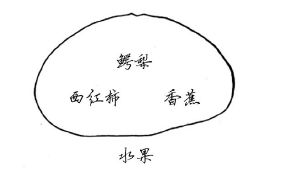
还有一个蔬菜集合。
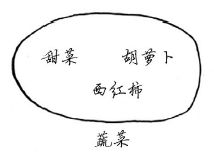
有这两个集合后,就可以使用它们来做些有趣的事情。
- 并集意味着将两个集合合并提出多出的共有元素(就是放在一起再集合一下)。
- 交集意味着找出两个集合中都有的元素(在这里,只有西红柿符合条件)。
- 差集意味着将从一个集合中剔除出现在另一个集合中的元素。
下面是一个例子。
>>> fruits = set(["avocado", "tomato", "banana"])
>>> vegetables = set(["beets", "carrots", "tomato"])
>>> fruits | vegetables # 并集
set(["avocado", "beets", "carrots", "tomato", "banana"])
>>> fruits & vegetables # 交集
set(["tomato"])
>>> fruits – vegetables # 差集
set(["avocado", "banana"])
>>> vegetables – fruits
这里小结一下:
- 集合类似于列表,只是不能包含重复的元素;
- 可执行一些有趣的集合运算,如并集、交集和差集。
4)回到代码
covered = states_needed & states_for_station
covered 是一个集合,包含同时出现在 states_needed 和 states_for_station 中的州;换言之,它包含当前广播台覆盖的
一系列还未覆盖的州!接下来,检查该广播台覆盖的州是否比 best_station 多。
if len(covered) > len(states_covered):
best_station = station
states_covered = covered
如果是这样的,就将 best_station 设置为当前广播台。最后,你在 for 循环结束后将 best_station 添加到最终的广播台列表中。
final_stations.add(best_station)
你还需更新 states_needed。由于该广播台覆盖了一些州,因此不用再覆盖这些州。
states_needed -= states_covered
你不断地循环,直到 states_needed 为空。这个循环的完整代码如下。
while states_needed:
best_station = None
states_covered = set()
for station, states in stations.items():
covered = states_needed & states
if len(covered) > len(states_covered):
best_station = station
states_covered = covered
states_needed -= states_covered
final_stations.add(best_station)
最后,你打印 final_stations,结果类似于下面这样。
>>> print final_stations
set(['ktwo', 'kthree', 'kone', 'kfive'])
python版本代码如下:
# 你传入一个数组,它被转换成一个集合。
states_needed = set(["mt", "wa", "or", "id", "nv", "ut", "ca", "az"])
stations = {}
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])
final_stations = set()
while states_needed:
best_station = None
states_covered = set()
for station, states in stations.items():
covered = states_needed & states
if len(covered) > len(states_covered):
best_station = station
states_covered = covered
states_needed -= states_covered
final_stations.add(best_station)
print(final_stations)
![]()
结果符合你的预期吗?选择的广播台可能是2、3、4和5,而不是预期的1、2、3和5。下面来比较一下贪婪算法和精确算法的运行时间。

五、NP 完全问题
为解决集合覆盖问题,你必须计算每个可能的集合。
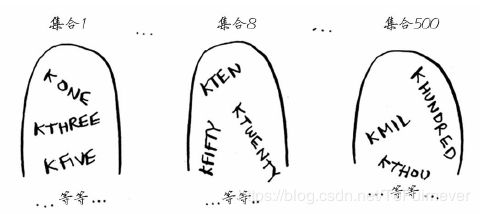
这可能让你想起了第1章介绍的旅行商问题(《算法图解》学习笔记(一):二分查找(附代码))。在这个问题中,旅行商需要前往5个不同的城市。
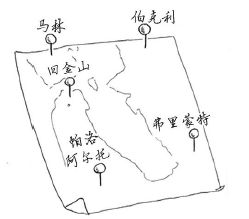
他需要找出前往这5个城市的最短路径,为此,必须计算每条可能的路径。
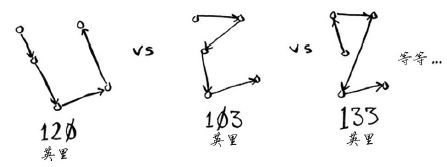
前往5个城市时,可能的路径有多少条呢?
1)旅行商问题详解
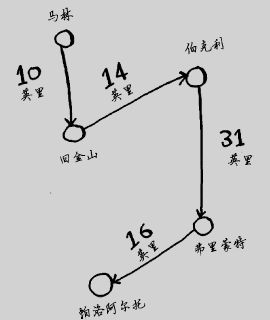
我们从城市数较少的情况着手。假设只涉及两个城市,因此可供选择的路线有两条。
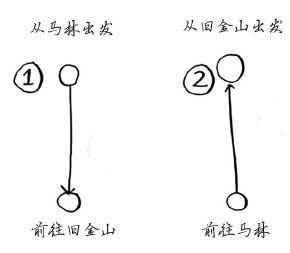
这两条路线相同还是不同?
你可能认为这两条路线相同,难道从旧金山到马林的距离与从马林到旧金山的距离不同吗?不一定。有些城市(如旧金山)有很多单行线,因此你无法按原路返回。你可能需要离开原路行驶一两英里才能找到上高速的匝道。因此,这两条路线不一定相同。
你可能心存疑惑:在旅行商问题中,必须从特定的城市出发吗?例如,假设我是旅行商。居住在旧金山,需要前往其他4个城市,因此将从旧金山出发。但有时候,不确定要从哪个城市出发。假设联邦快递将包裹从芝加哥发往湾区,包裹将通过航运发送到联邦快递在湾区的50个集散点之一,再装上经过不同配送点的卡车。该通过航运发送到哪个集散点呢?在这个例子中,起点就是未知的。因此,需要通过计算为旅行商找出起点和最佳路线。
在这两种情况下,运行时间是相同的。但出发城市未定时更容易处理,因此这里以这种情况为例。
涉及两个城市时,可能的路线有两条。
1。3个城市
现在假设再增加一个城市,可能的路线有多少条呢?
如果从伯克利出发,就需前往另外两个城市。
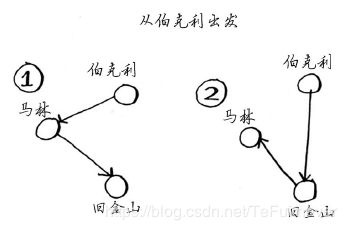
从每个城市出发时,都有两条不同的路线,因此总共有6条路线。

因此涉及3个城市时,可能的路线有6条。
2。4个城市
我们再增加一个城市——弗里蒙特。现在假设从弗里蒙特出发。

从弗里蒙特出发时,有6条可能的路线。这些路线与前面只有3个城市时计算的6条路线很像,只是现在所有的路线都多了一个城市——弗里蒙特!这里有一个规律。假设有4个城市,你选择一个出发城市——弗里蒙特后,还余下3个城市。而你知道,涉及3个城市时,可能的路线有6条。从弗里蒙特出发时,有6条可能的路线,但还可以从其他任何一个城市出发。

可能的出发城市有4个,从每个城市出发时都有6条可能的路线,因此可能的路线有4 × 6 = 24条。
你看出规律了吗?每增加一个城市,需要计算的路线数都将增加。

涉及6个城市时,可能的路线有多少条呢?如果你说720条,那就对了。7个城市为5040条,8个城市为40 320条。
这被称为 阶乘函数(factorial function),第3章(《算法图解》学习笔记(三):递归和栈(附代码))介绍过。5! = 120。假设有10个城市,可能的路线有多少条呢?10! = 3 628 800。换句话说,涉及10个城市时,需要计算的可能路线超过300万条。正如你看到的,可能的路线数增加得非常快!因此,如果涉及的城市很多,根本就无法找出旅行商问题的正确解。
旅行商问题和集合覆盖问题有一些共同之处:你需要计算所有的解,并从中选出最小/最短的那个。这两个问题都属于NP完全问题。
近似求解
对旅行商问题来说,什么样的近似算法不错呢?能找到较短路径的算法就算不错。在继续往下阅读前,看看你能设计出这样的算法吗?
采取这样的做法如何:随便选择出发城市,然后每次选择要去的下一个城市时,都选择还没去的最近的城市。假设旅行商从马林出发。
总旅程为71英里。这条路径可能不是最短的,但也相当短了。
NP完全问题 的简单定义是,以难解著称的问题,如 旅行商问题 和 集合覆盖问题。很多非常聪明的人都认为,根本不可能编写出可快速解决这些问题的算法。
2)如何识别 NP 完全问题
来看个例子,Jonah正为其虚构的橄榄球队挑选队员。他列了一个清单,指出了对球队的要求:优秀的四分卫,优秀的跑卫,擅长雨中作战,以及能承受压力等。他有一个候选球员名单,其中每个球员都满足某些要求。
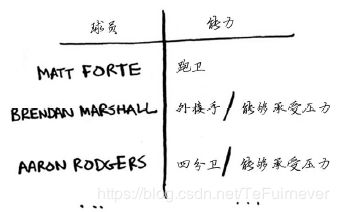
Jonah需要组建一个满足所有这些要求的球队,可名额有限。等等,Jonah突然间意识到,这不就是一个集合覆盖问题吗!
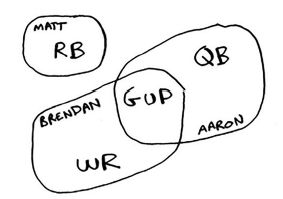
Jonah可使用前面介绍的近似算法来组建球队。
- 找出符合最多要求的球员。
- 不断重复这个过程,直到球队满足要求(或球队名额已满)。
NP完全问题无处不在!如果能够判断出要解决的问题属于NP完全问题就好了,这样就不用去寻找完美的解决方案,而是使用近似算法即可。但要判断问题是不是NP完全问题很难,易于解决的问题和NP完全问题的差别通常很小。例如,前一章深入讨论了最短路径(《算法图解》学习笔记(七):狄克斯特拉算法(附代码)),你知道如何找出从A点到B点的最短路径。
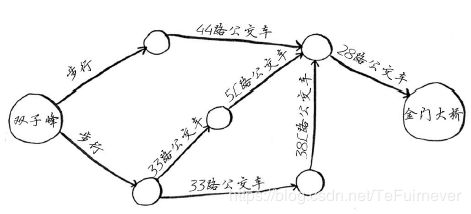
但如果要找出经由指定几个点的的最短路径,就是旅行商问题——NP完全问题。简言之,没办法判断问题是不是NP完全问题,但还是有一些蛛丝马迹可循的。
- 元素较少时算法的运行速度非常快,但随着元素数量的增加,速度会变得非常慢。
- 涉及“所有组合”的问题通常是NP完全问题。
- 不能将问题分成小问题,必须考虑各种可能的情况。这可能是NP完全问题。
- 如果问题涉及序列(如旅行商问题中的城市序列)且难以解决,它可能就是NP完全问题。
- 如果问题涉及集合(如广播台集合)且难以解决,它可能就是NP完全问题。
- 如果问题可转换为集合覆盖问题或旅行商问题,那它肯定是NP完全问题。
六、总结
- 贪婪算法寻找局部最优解,企图以这种方式获得全局最优解。
- 对于NP完全问题,还没有找到快速解决方案。
- 面临NP完全问题时,最佳的做法是使用近似算法。
- 贪婪算法易于实现、运行速度快,是不错的近似算法。
参考文章
- 《算法图解》