算法设计与分析：New 21 Game（Week 10）

学号：16340008

题目：837. New 21 Game

---

Question:

Alice plays the following game, loosely based on the card game "21".

Alice starts with 0 points, and draws numbers while she has less than K points.  During each draw, she gains an integer number of points randomly from the range [1, W], where W is an integer.  Each draw is independent and the outcomes have equal probabilities.

Alice stops drawing numbers when she gets K or more points.  What is the probability that she has N or less points?

Example 1:

Input: N = 10, K = 1, W = 10
Output: 1.00000
Explanation:  Alice gets a single card, then stops.

Example 2:

Input: N = 6, K = 1, W = 10
Output: 0.60000
Explanation:  Alice gets a single card, then stops.
In 6 out of W = 10 possibilities, she is at or below N = 6 points.

Example 3:

Input: N = 21, K = 17, W = 10
Output: 0.73278

Note:

1. 0 <= K <= N <= 10000
2. 1 <= W <= 10000
3. Answers will be accepted as correct if they are within 10^-5 of the correct answer.
4. The judging time limit has been reduced for this question.

---

Question:

这个问题类似经典的“爬楼梯”动态规划问题。该题的题意提取就是，从0开始每次能走1点到W点（随机，概率均等），当总点数大于等于K则停止，问最后一步走完后点数小于等于N的概率。在爬楼梯问题中，最后一步的函数值是由两步前与一步前的函数值相加得到。这道题类似，对于一个值 i（假设 i > W），它的上一步可以是 i - W 到 i - 1 任意一个，且这W个点每个点到 i 的概率都是 1 / W。因此我们定义到一个点 i 的概率为，则有：

类似的，若，则有

用语言来描述的话，就是把一个问题分成W个子问题分别求解，是十分常见的动态规划。

接下来我们考虑一些特殊情况：

• 当K是0，我们可以不加点就直接符合条件，则概率为100%（1）
• 当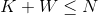，我们最后一次加点无论如何也无法超过N，因此概率也同样为1。

因此我们可以先在函数前方得到如下代码（python3）：

if K == 0 or K + W <= N :
    return 1.0

后面就是动态规划的设计。对于爬楼梯，我们可以自底向上也可以自顶向下，此题同理。这里我们采用自底向上来节省空间复杂度（即不采用递归，采用循环），实际上我们可以只用 W+1 个内存单位来存储数据，然而这样数据交换过程会消耗一定的时间（尽管不会反应到时间复杂度上）。因此这里我用一个长度为 n + 1的列表（数组）来存储数据（概率）。

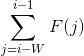回到刚刚的模型，当我们求完打算求的时候，我们能发现两者的差仅仅为（当 时则为，当时则为），因此我们可以用一个数 num 存储，以更快求出。我们可以在每次求解之后，对这个 num 更新为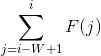，则每次求我们可以通过 直接获得。具体更新方法如下代码：

for i in range(1, N + 1) :
    p[i] = num / W
    if i >= W :
        num -= p[i - W]
    if i < K :
        num += p[i]

将代码整合得：

class Solution:
    def new21Game(self, N, K, W):
        """
        :type N: int
        :type K: int
        :type W: int
        :rtype: float
        """
        if K == 0 or K + W <= N :
            return 1.0

        p = [0.0] * (N + 1)
        p[0] = 1.0

        num = 1.0

        for i in range(1, N + 1) :
            p[i] = num / W
            if i >= W :
                num -= p[i - W]
            if i < K :
                num += p[i]

        return sum(p[K:])

 测试代码：

N = 21
K = 17
W = 10

test = Solution()
print(test.new21Game(N, K, W))

得到正确答案：

提交结果如下：