目标检测(object detection)系列(十一) RetinaNet:one-stage检测器巅峰之作
目标检测系列:
目标检测(object detection)系列(一) R-CNN:CNN目标检测的开山之作
目标检测(object detection)系列(二) SPP-Net:让卷积计算可以共享
目标检测(object detection)系列(三) Fast R-CNN:end-to-end的愉快训练
目标检测(object detection)系列(四) Faster R-CNN:有RPN的Fast R-CNN
目标检测(object detection)系列(五) YOLO:目标检测的另一种打开方式
目标检测(object detection)系列(六) SSD:兼顾效率和准确性
目标检测(object detection)系列(七) R-FCN:位置敏感的Faster R-CNN
目标检测(object detection)系列(八) YOLOv2:更好,更快,更强
目标检测(object detection)系列(九) YOLOv3:取百家所长成一家之言
目标检测(object detection)系列(十) FPN:用特征金字塔引入多尺度
目标检测(object detection)系列(十一) RetinaNet:one-stage检测器巅峰之作
目标检测(object detection)系列(十二) CornerNet:anchor free的开端
目标检测扩展系列:
目标检测(object detection)扩展系列(一) Selective Search:选择性搜索算法
目标检测(object detection)扩展系列(二) OHEM:在线难例挖掘
简介:one-stage检测器巅峰之作
在RetinaNet之前,目标检测领域一个普遍的现象就是two-stage的方法有更高的准确率,但是耗时也更严重,比如经典的Faster R-CNN,R-FCN,FPN等,而one-stage的方法效率更高,但是准确性要差一些,比如经典的YOLOv2,YOLOv3和SSD。这是两类方法本质上的思想不同带来这个普遍的结果,而RetinaNet的出现,在一定程度上改善了这个问题,让one-stage的方法具备了比two-stage方法更高的准确性,而且耗时更低。RetinaNet的论文是《Focal Loss for Dense Object Detection》。
RetinaNet原理
设计理念
two-stage方法会分两步完成目标检测,首先生产区域建议框,然后在对框做分类判别和回归矫正,而one-stage方法只有一步就完成了分类判别和bbox的回归。也就是因为这个不同,造成了上面的特点,首先耗时很好理解,因为two-stage有两步,而第二步的子网络要多次的重复输出,所以它不可避免的慢。那么造成two-stage效果好,one-stage效果偏差的本质原因是什么呢?
是因为anchor box后正负样本的严重不平衡问题导致的,我们举个例子说明有多不平衡,YOLOv2的anchor有845个,SSD的anchor有8732个,更多的anchor提供了更多的假设,对模型的召回率(尤其是小目标)有比较大的意义,但是一张正常的自然图像上,不会有这么多的目标的,这就势必会造成后续任务中的样本不平衡问题,而且由于是one-stage的,更多的anchor带来的好处和更严重的样本不平衡的矛盾没办法在结构上解决。
那么为什么two-stage方法不收影响呢?two-stage方法也有很多甚至更多的anchor啊,比如FRN有200k个,这和YOLOv2的8k个都不是一个量级了。因为是two-stage的结构,所以区域建议框可以选,想怎么选就怎么选,FRN在三个方面消除正负样本严重失衡的问题:
- FRN会选择与Ground turth的IOU>0.7的做正样本,与Ground turth的IOU<0.3的做负样本,这拉大正负样本间的差异;
- FRN的RPN最后的输出会控制在1000-2000个之间,控制样本数量;
- FRN组合每一次用于训练的minibatch,正负样本比例为1:3。
而就是因为one-stage的结构没办法二次筛选样本,那能不能总别的地方改进,进而减小这个影响。这个地方就是损失函数,因为样本的平衡与否,最终要影响要落下损失和优化上。所以RetinaNet提出了Focal loss,解决了正负样本区域极不平衡时目标检测loss易被大批量负样本所左右的问题。
Focal loss
Focal Loss是一种改进的交叉熵损失,一般情况下交叉熵损失在二分类时长这样:
C E ( p , y ) = − [ y l o g ( p ) + ( 1 − y ) l o g ( 1 − p ) ] CE(p,y)=-[ylog(p)+(1-y)log(1-p)] CE(p,y)=−[ylog(p)+(1−y)log(1−p)]
换一种形式,就变成这样:
C E ( p , y ) = { − l o g ( p ) i f ( y = 1 ) − l o g ( 1 − p ) o t h e r w i s e CE(p,y)=\left\{\begin{matrix} -log(p) &if (y=1) \\ -log(1-p) & otherwise \end{matrix}\right. CE(p,y)={−log(p)−log(1−p)if(y=1)otherwise
定义 p t p_{t} pt:
p t = { p i f ( y = 1 ) 1 − p o t h e r w i s e p_{t}=\left\{\begin{matrix} p &if (y=1) \\ 1-p & otherwise \end{matrix}\right. pt={p1−pif(y=1)otherwise
那么 C E ( p , y ) = C E ( p t ) = − l o g ( p t ) CE(p,y)=CE(p_{t})=-log(p_{t}) CE(p,y)=CE(pt)=−log(pt)。
平衡交叉熵损失的一般做法是为正例引入一个因子 α ∈ [ 0 , 1 ] \alpha\in[0,1] α∈[0,1],那么对应的,负例的因子就是 1 − α 1-\alpha 1−α。这里需要注意一下,文中提到了定义因子 α t \alpha_{t} αt的方式和定义 p t p_{t} pt是相似的,也就说是:
α t = { α i f ( y = 1 ) 1 − α o t h e r w i s e \alpha_{t}=\left\{\begin{matrix} \alpha &if (y=1) \\ 1-\alpha & otherwise \end{matrix}\right. αt={α1−αif(y=1)otherwise
有了这个 α t \alpha_{t} αt之后,平衡交叉熵损失才可以写为:
C E ( p t ) = − α t l o g ( p t ) CE(p_{t})=-\alpha_{t}log(p_{t}) CE(pt)=−αtlog(pt)
这个公式展开之后其实是这样的:
C E ( p , y ) = − { α l o g ( p ) i f ( y = 1 ) ( 1 − α ) l o g ( 1 − p ) o t h e r w i s e CE(p,y)=-\left\{\begin{matrix} \alpha log(p) &if (y=1) \\ (1-\alpha)log(1-p) & otherwise \end{matrix}\right. CE(p,y)=−{αlog(p)(1−α)log(1−p)if(y=1)otherwise
但是 α \alpha α是个固定的系数,它没办法去区分哪些样本难,哪些样本容易,所以在平衡交叉熵的基础上,Focal loss做了改进,进入 ( 1 − p t ) γ (1-p_{t})^{\gamma } (1−pt)γ,其中 γ \gamma γ是一个超参数,所以Focal loss的表达式就是:
F L ( p t ) = ( 1 − p t ) γ l o g ( p t ) FL(p_{t})=(1-p_{t})^{\gamma }log(p_{t}) FL(pt)=(1−pt)γlog(pt)
那为啥这样的形式就比平衡交叉熵好呢?我们假设 γ \gamma γ为1,系数就变成了 1 − p t 1-p_{t} 1−pt,在这个基础上,我们按照上面的方式展开 F L ( p t ) FL(p_{t}) FL(pt),其实就是这样子:
F L ( p , y ) = − { ( 1 − p ) l o g ( p ) i f ( y = 1 ) p l o g ( 1 − p ) o t h e r w i s e FL(p,y)=-\left\{\begin{matrix} (1-p) log(p) &if (y=1) \\ p log(1-p) & otherwise \end{matrix}\right. FL(p,y)=−{(1−p)log(p)plog(1−p)if(y=1)otherwise
由于交叉熵前做了softmax,所以 p p p一定是个正数,这个因子加上不会改变原有损失的符号,然后我们举例说明它怎么区分难易样本, p p p是正样本的预测值:
- 对于一个正例,模型认为它简单,那么 p p p会趋近于1, 1 − p 1-p 1−p会趋近于0,损失就会变小,相反的就会变大。
- 对于一个负例,模型认为它简单,那么 p p p会趋近于0,损失就会变小,相反的就会变大。
这就对模型的难易做出了不同的loss值,此外Focal loss还有一个超参数 γ \gamma γ,它起到了对因子成幂次,由于底数一定是一个小于1的数,幂次会拉大 1 − p t 1-p_{t} 1−pt原有的线性倍率。比如 1 − p t 1-p_{t} 1−pt原本是0.1和0.9, γ = 2 \gamma=2 γ=2时,会变成0.01和0.81,9倍变成了81倍。这种抑制简单样本,促进难样本的方式,其实和IOU>0.7和IOU<0.3有异曲同工之妙。
加了这东西之后,难易样本区分开了,但是负样本多的问题好像并没有解决掉,所以Focal loss最后又把平衡交叉熵加了回来,实验的时候使用的Focal loss形式是:
F L ( p t ) = α t ( 1 − p t ) γ l o g ( p t ) FL(p_{t})=\alpha_{t}(1-p_{t})^{\gamma }log(p_{t}) FL(pt)=αt(1−pt)γlog(pt)

这个实验说明了 α \alpha α和 γ \gamma γ选取,在(a)中,对于平衡交叉熵损失,在 α = 0.75 \alpha=0.75 α=0.75时,效果是最好的,这符合我们在上面分析的结果, α > 0.5 \alpha>0.5 α>0.5可以抑制负样本,但是在Focal loss中, α = 0.25 \alpha=0.25 α=0.25和 γ = 2 \gamma=2 γ=2的时候,效果最好,这可能是因为 ( 1 − p t ) γ (1-p_{t})^{\gamma } (1−pt)γ的引入,影响了 α \alpha α的选取。
Focal loss是RetinaNet最重要的部分,网络结构、Anchor、损失等其余的东西RetinaNet用的都是之前,我们简单提一下吧。
网络结构

这个是RetinaNet的网络结构,其实就是个FPN,但是它要用FPN做one-stage结构,而不再是two-stage,于是第二个阶段就被省略掉了。在YOLO的文章中,我们就说起过RPN和YOLO的区别,当RPN不再只做有没有物体的分类,而是做是什么物体的类别判断,那一个RPN就能完成整套目标检测任务。
这个思路就在RetinaNet里被使用了,RetinaNet中相当于舍弃了FPN中的Fast R-CNN,改变了FPN中的RPN网络直接做类别的预测。所以RetinaNet中也是有很多子网络的,对应了特征金字塔的层数。
至于更多细节的东西,就不做介绍了。
Anchor Box
RetinaNet选取Anchor Box的策略和FPN相似,一共有5个不同尺度的特征图,分别是 3 2 2 − 51 2 2 32^{2}-512^{2} 322−5122,每一层会有三种比例,所以FPN有15种Anchor,但是RetinaNet在这个基础上又加了一个因素,就是每一层特征图上还有一个尺度,它分别是该层特征图尺度的 2 0 , 2 1 3 , 2 2 3 {2^{0},2^{\frac{1}{3}},2^{\frac{2}{3}}} 20,231,232,于是RetinaNet的Anchor变成了45个。因为Focal loss的引入,让Anchor的选取变得为所欲为,就是不怕多。╮( ̄▽  ̄)╭
RetinaNet性能评价
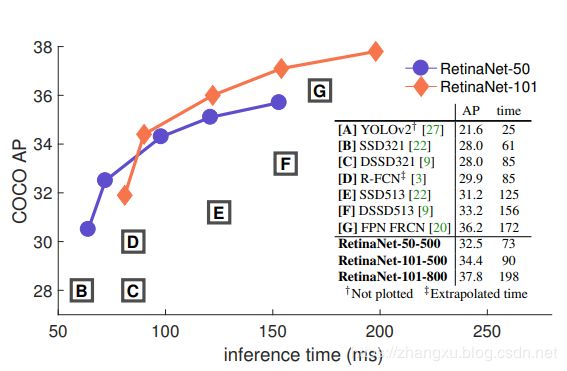
这个是RetinaNet的总体结果,在backbone选择ResNet-101,输入分辨率为800时,RetinaNet的AP超过了FPN,虽然比FPN还要慢些,但是这是one-stage的模型第一次使用同样输入分辨率和backbone的情况下,AP可以超过two-stage。当分辨率变成500的时候,RetinaNet具备了很优越的性能。