粒子群优化 (PSO) 在三维正弦波函数中的应用
在这篇博客中,我们将展示如何使用粒子群优化(PSO)算法求解三维正弦波函数,并通过增加正弦波扰动,使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程,并展示搜索空间中的动态过程和收敛曲线。
1. 目标函数定义
我们使用的目标函数是一个三维正弦波函数,定义如下:
objectiveFunc = @(x) sin(sqrt(x(1).^2 + x(2).^2)) + 0.5 * sin(5 * (x(1) + x(2)));
- 第一个项
sin(sqrt(x(1)^2 + x(2)^2))描述了基于 x(1)x(1)x(1) 和 x(2)x(2)x(2) 的三维正弦波。 - 第二个项
0.5 * sin(5 * (x(1) + x(2)))添加了一个周期为5倍的扰动,以增加搜索空间的复杂性。
2. 粒子群优化(PSO)参数设置
粒子群优化是一种基于群体智能的优化算法。以下是我们在这次实验中使用的PSO参数:
numParticles = 30; % 粒子数量
maxIter = 300; % 最大迭代次数
dim = 2; % 变量维度 (x, y)
w = 0.7; % 惯性权重
c1 = 1.5; % 个体学习因子
c2 = 1.5; % 群体学习因子
lb = [-10, -10]; % 搜索范围下限
ub = [10, 10]; % 搜索范围上限
3. 粒子初始化与搜索空间的可视化
我们首先初始化粒子的初始位置和速度,并随机生成每个粒子的历史最佳位置和全局最佳位置。
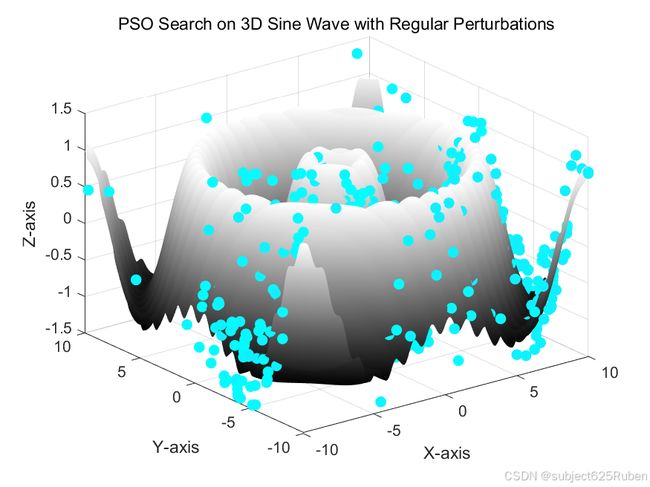
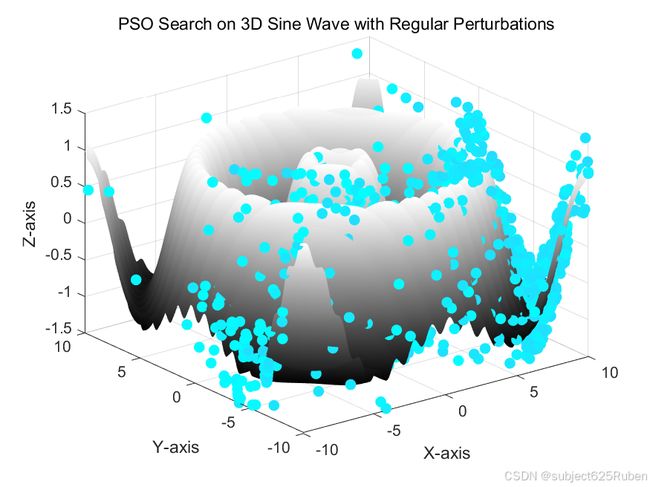
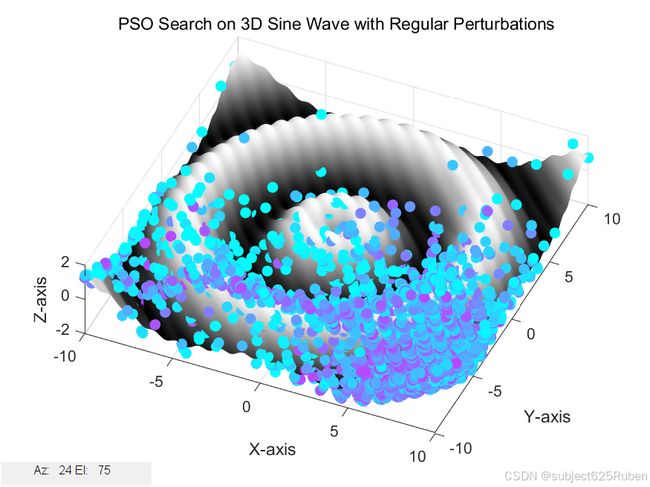
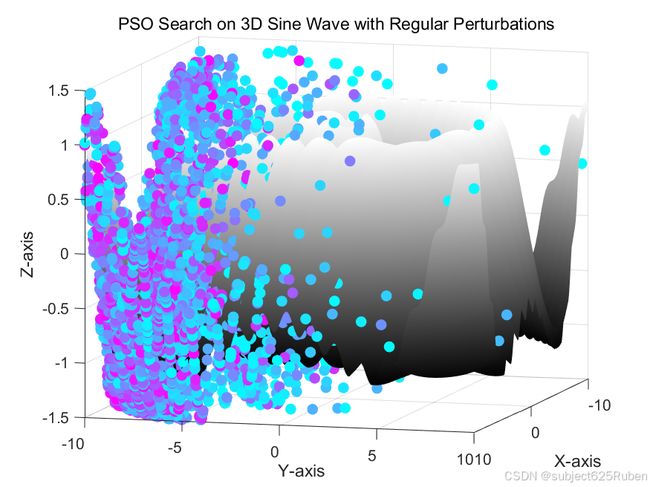
接下来,我们使用 meshgrid 和 surf 函数绘制目标函数的三维图像,以便观察PSO算法在搜索空间中的行为:
[x, y] = meshgrid(-10:0.1:10, -10:0.1:10);
z = sin(sqrt(x.^2 + y.^2)) + 0.1 * sin(5 * (x + y)); % 目标函数
surf(x, y, z);
title('PSO Search on 3D Sine Wave with Regular Perturbations');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');
colormap gray;
shading interp;
4. PSO 迭代过程
在每次迭代中,粒子的速度和位置都会根据惯性权重、个体最佳位置和全局最佳位置来更新。我们还会根据当前的目标函数值来判断粒子是否找到了更好的位置,并动态调整它们的历史最佳值。
以下是粒子位置和速度的更新公式:
vel = w * vel + c1 * r1 .* (pbest - pos) + c2 * r2 .* (gbest - pos);
pos = pos + vel;
我们在每次迭代时绘制粒子的动态搜索路径,并使用 cool 配色方案来展示粒子位置的变化。
scatter3(pos(:, 1), pos(:, 2), arrayfun(@(i) objectiveFunc(pos(i, :)), 1:numParticles), ...
50, colorMap(iter, :), 'filled');
为更好地观察搜索过程,我们将每20次迭代保存一张图像:
if mod(iter, 20) == 0
filename = sprintf('PSO_Iteration_%d.png', iter);
saveas(gcf, filename); % 保存图像
end
5. 收敛曲线
最后,我们绘制了PSO算法的收敛曲线,用于显示全局最佳值在每次迭代过程中的变化:
plot(gbestValHistory, 'LineWidth', 2);
title('PSO Convergence Curve');
xlabel('Iteration');
ylabel('Global Best Value');
grid on;
通过收敛曲线,我们可以直观地看到PSO算法在求解过程中如何逐渐收敛到最优解。
6. 结论
这次实验通过粒子群优化算法成功求解了三维正弦波函数的最优解,并动态展示了粒子在复杂的搜索空间中的搜索路径。PSO算法凭借其简单、快速的优势,在这类优化问题中表现出了良好的收敛性和稳定性。
% 目标函数定义:三维正弦波函数(增加有规律的正弦波波动)
objectiveFunc = @(x) sin(sqrt(x(1).^2 + x(2).^2)) + 0.5 * sin(5 * (x(1) + x(2)));
% PSO 参数设置
numParticles = 30; % 粒子数量
maxIter = 300; % 最大迭代次数
dim = 2; % 变量维度 (x, y)
w = 0.7; % 惯性权重
c1 = 1.5; % 个体学习因子
c2 = 1.5; % 群体学习因子
lb = [-10, -10]; % 搜索范围下限
ub = [10, 10]; % 搜索范围上限
% 初始化粒子位置和速度
pos = repmat(lb, numParticles, 1) + rand(numParticles, dim) .* repmat(ub - lb, numParticles, 1);
vel = zeros(numParticles, dim);
pbest = pos; % 每个粒子的历史最佳位置
pbestVal = arrayfun(@(i) objectiveFunc(pbest(i, :)), 1:numParticles); % 每个粒子的历史最佳值
[~, gbestIdx] = min(pbestVal); % 找到全局最佳粒子索引
gbest = pbest(gbestIdx, :); % 全局最佳位置
% 保存迭代过程中全局最优值
gbestValHistory = zeros(maxIter, 1);
% 绘制搜索空间(目标函数)图像
figure;
[x, y] = meshgrid(-10:0.1:10, -10:0.1:10);
z = sin(sqrt(x.^2 + y.^2)) + 0.1 * sin(5 * (x + y)); % 目标函数
surf(x, y, z);
hold on;
title('PSO Search on 3D Sine Wave with Regular Perturbations');
xlabel('X-axis');
ylabel('Y-axis');
zlabel('Z-axis');
colormap gray; % 使用 gray 配色
shading interp;
% PSO迭代过程
colorMap = cool(maxIter); % 使用 cool 配色方案
for iter = 1:maxIter
% 更新粒子速度和位置
r1 = rand(numParticles, dim);
r2 = rand(numParticles, dim);
vel = w * vel + c1 * r1 .* (pbest - pos) + c2 * r2 .* (gbest - pos);
pos = pos + vel;
% 边界处理
pos = max(pos, repmat(lb, numParticles, 1));
pos = min(pos, repmat(ub, numParticles, 1));
% 计算新的目标函数值
fVal = arrayfun(@(i) objectiveFunc(pos(i, :)), 1:numParticles);
% 更新每个粒子的历史最佳位置和全局最佳位置
betterMask = fVal < pbestVal;
pbest(betterMask, :) = pos(betterMask, :);
pbestVal(betterMask) = fVal(betterMask);
[minVal, minIdx] = min(pbestVal);
if minVal < objectiveFunc(gbest)
gbest = pbest(minIdx, :);
end
% 保存全局最佳值历史
gbestValHistory(iter) = objectiveFunc(gbest);
% 使用 cool 配色显示当前迭代的粒子位置
scatter3(pos(:, 1), pos(:, 2), arrayfun(@(i) objectiveFunc(pos(i, :)), 1:numParticles), ...
50, colorMap(iter, :), 'filled'); % 动态颜色变化
pause(0.1); % 延时以便观察动态过程
% 每20次迭代保存当前图像
if mod(iter, 20) == 0
filename = sprintf('PSO_Iteration_%d.png', iter);
saveas(gcf, filename); % 保存图像
end
end
hold off;
% 绘制收敛曲线
figure;
plot(gbestValHistory, 'LineWidth', 2);
title('PSO Convergence Curve');
xlabel('Iteration');
ylabel('Global Best Value');
grid on;