奇异值分解(SVD)与图像压缩(附Python代码实现)
1. SVD图像压缩原理介绍
奇异值分解(singular value decomposition,SVD)是线性代数中一种重要的矩阵分解,在信号处理、统计学等领域有重要应用。
假设 M M M是一个 m × n m \times n m×n阶矩阵,其中的元素全部属于域 K K K,也就是实数域或复数域。如此则存在一个分解使得
(1) M = U Σ V ∗ M = U\Sigma {V^ * } \tag {1} M=UΣV∗(1)
其中 U U U是 m × m m \times m m×m阶酉矩阵; Σ \Sigma Σ是 m × n m \times n m×n阶非负实数对角矩阵;而 V ∗ {V^ * } V∗为矩阵 V V V的共轭转置矩阵,是 n × n n \times n n×n阶酉矩阵。这样的分解就称为矩阵 M M M的奇异值分解。 Σ \Sigma Σ对角线上的元素 Σ i , i {\Sigma _{i,i}} Σi,i即为矩阵 M M M的奇异值。其具体分解形式为:
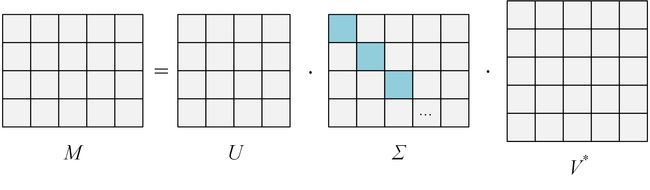
上面的示意图,可以用数学公式来表示,如下所示:
(2) M = [ u 1 , u 2 , … , u m ] [ D 0 0 0 ] [ v 1 ⊤ v 2 ⊤ ⋮ v n ⊤ ] M = \left[ {{u_1},{u_2}, \ldots ,{u_m}} \right]\begin{bmatrix} D & 0\\ 0 & 0 \end{bmatrix} \begin{bmatrix} v_1^ \top \\ v_2^ \top \\ \vdots \\ v_n^ \top \end{bmatrix} \tag {2} M=[u1,u2,…,um][D000]⎣⎢⎢⎢⎡v1⊤v2⊤⋮vn⊤⎦⎥⎥⎥⎤(2)
其中,
(3) D = [ σ 1 0 ⋯ 0 0 σ 2 ⋮ 0 ⋮ ⋮ ⋱ ⋮ 0 0 ⋯ σ r ] D = {\begin{bmatrix} {{\sigma _1}}&0& \cdots &0\\ 0&{{\sigma _2}}& \vdots &0\\ \vdots & \vdots & \ddots & \vdots \\ 0&0& \cdots &{{\sigma _r}} \end{bmatrix}} \tag {3} D=⎣⎢⎢⎢⎢⎡σ10⋮00σ2⋮0⋯⋮⋱⋯00⋮σr⎦⎥⎥⎥⎥⎤(3)
将矩阵 M M M展开,可得:
(4) M = σ 1 u 1 v 1 ⊤ + σ 2 u 2 v 2 ⊤ + ⋯ + σ r u r v r ⊤ M = {\sigma _1}{u_1}v_1^ \top + {\sigma _2}{u_2}v_2^ \top + \cdots + {\sigma _r}{u_r}v_r^ \top \tag {4} M=σ1u1v1⊤+σ2u2v2⊤+⋯+σrurvr⊤(4)
在上述奇异值分解 M = U Σ V ∗ M = U\Sigma {V^ * } M=UΣV∗中,
- V V V的列(rows)组成一套对 M M M的正交"输入"或"分析"的基向量。这些向量是 M ∗ M M^*M M∗M的特征向量。
- U U U的列(rows)组成一套对 M M M的正交"输出"的基向量。这些向量是 M M ∗ MM^* MM∗的特征向量。
- Σ Σ Σ对角线上的元素是奇异值,可视为是在输入与输出间进行的标量的"膨胀控制"。这些是 M M ∗ MM^* MM∗及 M ∗ M M^*M M∗M的特征值的非负平方根,并与 U U U和 V V V的行向量相对应。
现在我们分析奇异值分解的几何意义,因为矩阵 U U U和矩阵 V V V都是酉矩阵,而矩阵 U U U的列向量 u 1 , u 2 , … u m {u_1},{u_2}, \ldots {u_m} u1,u2,…um组成了 K m {K^m} Km空间的一组标准正交基。同理,矩阵 V V V的列向量 v 1 , v 2 , … v n {v_1},{v_2}, \ldots {v_n} v1,v2,…vn也组成了 K n {K^n} Kn空间的一组标准正交基(根据向量空间的标准点积法则)。矩阵 M M M代表从 K n {K^n} Kn到 K m {K^m} Km的一个线性映射 T {\mathcal T} T : x → M x x \to Mx x→Mx。通过这些标准正交基,这个变换可以用很简单的方式进行描述: T ( v i ) = σ i u i , i = 1 , … , min ( m , n ) {\mathcal T}({v_i}) = {\sigma _i}{u_i},i = 1, \ldots ,\min (m,n) T(vi)=σiui,i=1,…,min(m,n),其中 σ i {\sigma _i} σi是 Σ \Sigma Σ中的第 i i i个对角元。当 i > min ( m , n ) i > \min (m,n) i>min(m,n)时,有 T ( v i ) = 0 {\mathcal T}({v_i}) = 0 T(vi)=0。
这样,SVD分解的几何意义可以理解为:对于每一个线性映射 T : K n → K m {\mathcal T}:{K^n} \to {K^m} T:Kn→Km, T {\mathcal T} T的奇异值分解在原空间与像空间中分别找到一组标准正交基,使得 T {\mathcal T} T把 K n {K^n} Kn的第 i i i个基向量映射为 K m {K^m} Km的第 i i i个基向量的非负倍数,并将 K n {K^n} Kn中余下的基向量映射为零向量。换句话说,线性变换 T {\mathcal T} T在这两组选定的基上的矩阵表示为所有对角元均为非负数的对角矩阵。
如果我们将展开的矩阵 M M M看作为一个图像的矩阵,则展开式中的每一个分量按 σ i \sigma_i σi的大小排序, σ i \sigma_i σi越大,说明越重要。而后面的权重很小,可以舍去,如果只取前面 k k k项,则数据量为 ( m + n + 1 ) k ≪ m n ( m + n + 1 ) k ≪ m n \left( {m + n + 1} \right)k \ll mn\left( {m + n + 1} \right)k \ll mn (m+n+1)k≪mn(m+n+1)k≪mn。这些保留的数据代表了原始图像中最主要、最具代表性的信息。 这也就是图像压缩的基本原理。
2. 基于Python的代码实现
- 运行环境介绍:Python 3.x
- 源码出处:基于Python查看SVD压缩图片的效果 ,非常感谢moverzp同学的无私贡献!
源码为单文件Python代码,如下所示:
from PIL import Image
import numpy as np
def rebuild_img(u, sigma, v, p): #p表示奇异值的百分比
print (p)
m = len(u)
n = len(v)
a = np.zeros((m, n))
count = (int)(sum(sigma))
curSum = 0
k = 0
while curSum <= count * p:
uk = u[:, k].reshape(m, 1)
vk = v[k].reshape(1, n)
a += sigma[k] * np.dot(uk, vk)
curSum += sigma[k]
k += 1
print ('k:',k)
a[a < 0] = 0
a[a > 255] = 255
#按照最近距离取整数,并设置参数类型为uint8
return np.rint(a).astype("uint8")
if __name__ == '__main__':
img = Image.open('Demo.jpg', 'r')
a = np.array(img)
for p in np.arange(0.1, 1, 0.1):
u, sigma, v = np.linalg.svd(a[:, :, 0])
R = rebuild_img(u, sigma, v, p)
u, sigma, v = np.linalg.svd(a[:, :, 1])
G = rebuild_img(u, sigma, v, p)
u, sigma, v = np.linalg.svd(a[:, :, 2])
B = rebuild_img(u, sigma, v, p)
I = np.stack((R, G, B), 2)
#保存图片在img文件夹下
Image.fromarray(I).save("img\\svd_" + str(p * 100) + ".jpg")
运行后生成的各种不同程度的压缩图像如下所示:
可以看出, k k k的取值越大,压缩后还原的图像质量越高。
参考资料:
- 基于奇异值分解的图像压缩
- 基于Python查看SVD压缩图片的效果
- Wikipedia - 奇异值分解




