十一、改变神经网络的学习方法（5）：随机梯度下降的变化形式(Adagrad、RMSProp、Adadelta、Momentum、NAG)

本篇博客主要内容参考图书《神经网络与深度学习》，李航博士的《统计学习方法》National Taiwan University (NTU)李宏毅老师的《Machine Learning》的课程，在下文中如果不正确的地方请积极指出。
如果喜欢请点赞，欢迎评论留言 ！ o(￣▽￣)ブ

  在本小节主要对训练神经网络代价函数的梯度下降算法及其变形进行讲解。因为随机梯度只是将用整体数据改变为采用部分数据训练，其主体仍是梯度下降方法，所以从梯度下降算法出发，介绍算法的来源及实现，再根据梯度下降算法学习率固定且迭代次数长的缺点引出两类改进的方法。一类是可以自动调整学习率的Adagrad；但是Adagrad将所有的历史信息统一看待，针对这样的不足引出了RMSProp方法；另一类是利用二阶导数信息的牛顿法，但是牛顿法具有计算复杂度高等较大的缺点，进而引出了可以利用导数变化信息但是无需计算海森矩阵的Momentum方法。最后将RMSProp与Momentum方法结合得到Adam方法。

1. 梯度下降方法回顾

  首先讲述为什么梯度下降方法可以使得损失函数的值下降，将代价函数抽象为关于统一参数 w=(w1,w2,...,wn) w = ( w 1 , w 2 , . . . , w n ) 的代价函数 C(w) C ( w ) ，其中的参数 w w 包括了原始神经网络中权值和偏置在内的所有参数，借助泰勒展开式，代价函数可以在点 w0 w 0 处被近似为

C(w0+Δw)≈C(w0)+∑j∂C∂wjΔwj C ( w 0 + Δ w ) ≈ C ( w 0 ) + ∑ j ∂ C ∂ w j Δ w j

因此可以得到

ΔC≈∇CΔw Δ C ≈ ∇ C Δ w

当 Δw=−η∇C Δ w = − η ∇ C 时，可以得到

ΔC≈−η∇C2 Δ C ≈ − η ∇ C 2

代价函数的值总是在下降的过程中，因此这个方法时可行的（具体的推导过程及如何通过反向传播算法实现可以参照《三、梯度下降与反向传播（含过程推导及证明）》。在神经网络中使用梯度下降法去寻找权重 w w 和偏置 b b 减小代价函数，具体表现是

⎧⎩⎨⎪⎪wk→w′k=wk−η∂C∂wkbl→b′l=bl−η∂C∂bl { w k → w k ′ = w k − η ∂ C ∂ w k b l → b l ′ = b l − η ∂ C ∂ b l

用一个过程图体现就是如下图

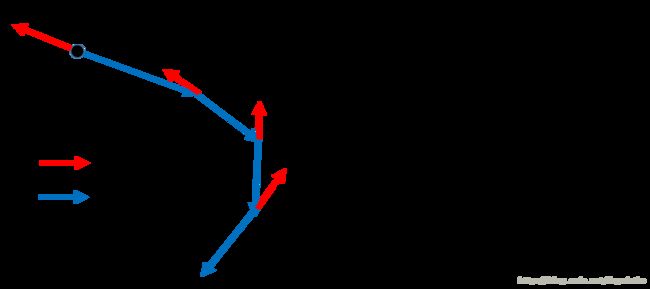
图1 .梯度下降过程示意图

在上图中，红色的方向为计算出的梯度方向，蓝色方向是参数实际移动的方向，参数 w w 按照公式 X 的移动的过程即如上所示。
  但是这样的方法有三个明显的局限性，第一个局限性在于在学习的过程中学习率 η η 是固定的，无法根据神经网络训练的程度调整参数；其次在这里只用到了梯度，但是没有用到梯度的变化情况，因此再求函数最优质的过程中走的并不是最短距离；最后该方法明显在高原、鞍点以及局部最小点处表现不佳。因此在接下来的部分分别从改进学习率和利用梯度变化情况两个方面介绍基于梯度下降的改进方法。

2. 改进学习率

  在上述的梯度下降方法中，学习率是一个定值，不会随着神经网络的学习而发生改变，如下图所示

图2 .不同学习率对于训练过程的影响

从上图中可以看到，如果学习率是按照红色箭头的值设定的，在迭代的过程中正好可以达到全局最优解；但是如果学习率的值设的比较小，去蓝色的箭头所示，虽然可以肯定会达到最优解，但是速度却十分缓慢；若加大学习率，很有可能像绿色箭头那样一直在某一个值附近震荡，或者像黄色的箭头那样直接发散出去，所以选择合适的学习率是十分重要的。上图中左侧的图只是针对具有一个参数的模型，对于神经网络这种多参数的是无法画出左侧这种曲线的，因此需要通过损失函数随迭代次数变化的曲线来判断神经网络的学习情况。如上图的右图所示，我们需要做的就是找到类似与红色曲线所对应的学习率。
  为达到上述的效果，在这里可以选用一种自动调整学习率的方法。这种方法要达到的目标是在开始的时候具有较大的学习率，但是随着迭代次数的增加，学习率逐渐下降，以便精准的达到的最优值。

2.1 Adagrad

  Adagrad就是一种可以满足上述要求的自动调节学习率的方法。它的过程如下所示

⎧⎩⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪ηt=ηt+1√σt=1t+1∑ti=0(gi)2−−−−−−−−−−−√wt+1=wt−ηtσtgt { η t = η t + 1 σ t = 1 t + 1 ∑ i = 0 t ( g i ) 2 w t + 1 = w t − η t σ t g t

通过化简，基于Adagrad的梯度下降法的更新规则如下

wt+1=wt−η∑ti=0(gi)2−−−−−−−−√gt w t + 1 = w t − η ∑ i = 0 t ( g i ) 2 g t

其中 gi g i 是每一次计算处的梯度值，现在每一权重的学习率都与他们之前的梯度值有关，因此在Adagrad中，每个参数都有属于自己的学习率。在这里有一个很奇特的现象，就是在 wt+1 w t + 1 的更行过程中， gi g i 的值越大，参数学习的速度越快，这是显而易见的；但是我们可以注意到， gi g i 的值越大分母的值也越大，会使学习的速度下降，这两个部分明明作用是相反的。为了理解为什么要这么做，我们从两种不同的角度进行考虑。
  第一种角度认为这是在描述当前的学习率与之前的学习率相比，他们的反差（Surprise）有多大，以其中的一个参数为例，列出下表进行比较

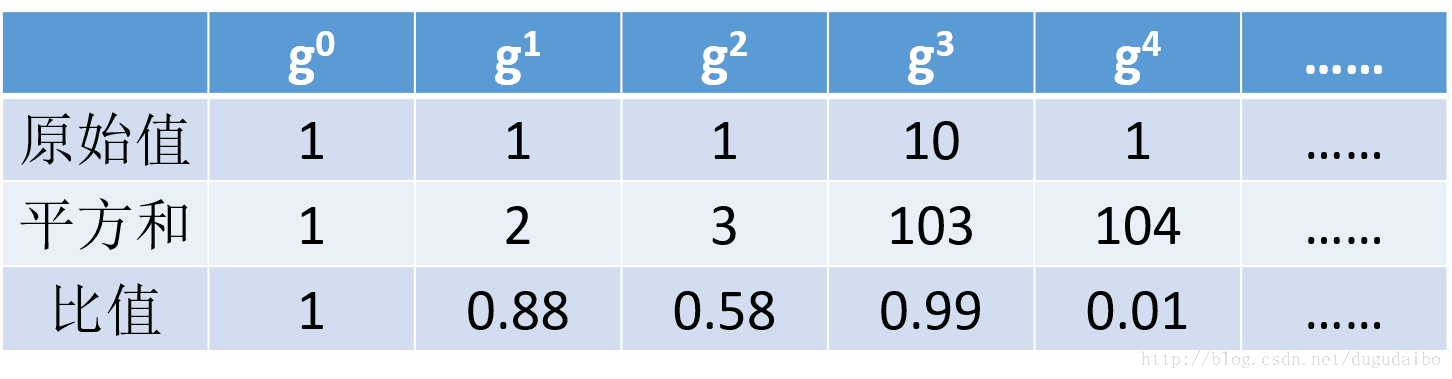
从上面的表我们可以看到，如果梯度保持一个相对稳定的值，如梯度的值一直是1，则学习的速度会逐渐下降，但是如果有一个明显的上升，此时学习率也会有较大的提升，而当提升之后梯度的值又下降的话学习率也会明显下降，因此可以看出其主要体现出的是与之前梯度的差异情况。

  第二个角度是从梯度的角度考虑。我们先仅仅考虑一个二次函数，如下图所示

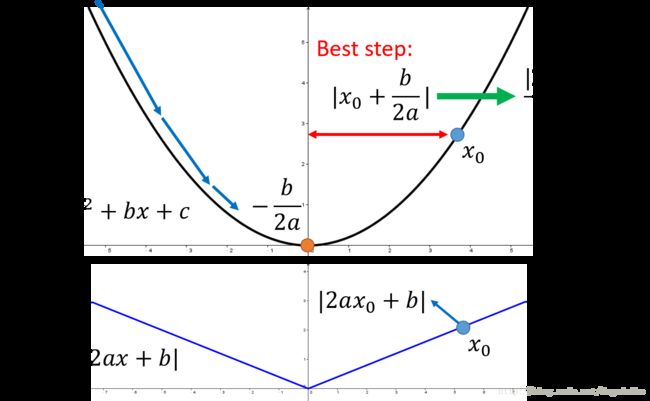
图3 . 二次函数中的梯度下降法

根据上图可以了看到，对于一个二次函数，最低点位于 −b2a − b 2 a ，因此位于 x0 x 0 处的点只需要移动 |x0+b2a| | x 0 + b 2 a | 就可以直接达到最小值，化简之后得到步长为 |2ax0+b|2a | 2 a x 0 + b | 2 a ，注意其中的分子是二次函数的一次微分值（也就是梯度下降法中的梯度），函数的一次微分值越大，那么该点距离最低点的距离也就越远，这个是显而易见的，但是实际上这只是对一元函数是有效的。我们考虑二元函数，绘制出其随两个自变量变化的等高图如下

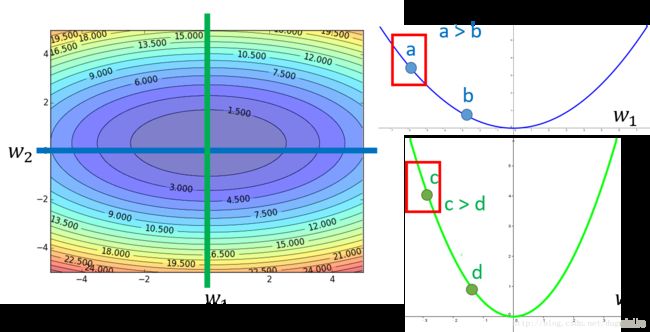
图4 .二元函数等高线随自变量变化情况

其中蓝色的曲线表示当参数 w2 w 2 固定的时候，函数的值随着参数 w1 w 1 的变化情况；而绿色的曲线表示当参数 w1 w 1 固定的时候，函数的值随着参数 w2 w 2 的变化情况。我们可以看到在蓝色的曲线中有 a a 和 b b 两个点， a a 的导数值明显大于 b b 点，且距离函数的最低点也更远，这似乎与之前的得到的结论是一样的。但是如果同时参考绿色曲线，情况就不一样了，我们看到 c c 点的导数值虽然明显大于 a a ，但是实际上从全局的角度看，它距离最低点反而要比 a a 点近。所以当考虑所有的参数（或者理解为从全局的角度出发），并不是导数值越大，更新参数迈出的那一步越大。
  重新观察之前的化简后得到的步长，发现不仅在分子位置包含了一次导数，在分母的位置还包括二次导数，因此更新的过程中不仅仅与一次导数有关，而且与二次导数有关。蓝色的曲线虽然一次导数小，但是还需要除以一个较小的二次导数，因此步长较大，绿色曲线虽然一次导数值大，但是二次导数值也大，所以步长反而较小。所以在梯度下降的过程中，不应仅仅使用一次导数的信息，还应该使用二次导数的信息。然而在神经网络中求二阶导数的计算量是十分庞大的，因此只能采用近似计算的方法，如下图所示

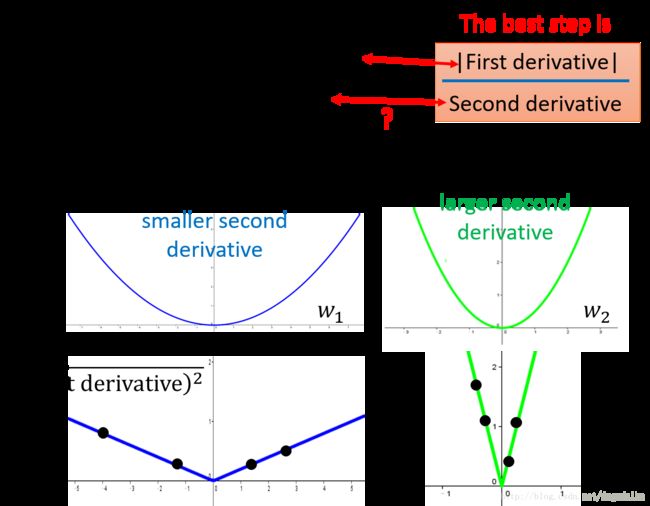
图5 . 从Adagrad的分母看作是对于二次导数值的采样

从上可以看到，下面的两个直线是上面二次函数的导数的绝对值的曲线。而二次导数相当于这些直线的斜率，虽然我们不能直接的求取这些直线的斜率，但是我们可以通过在这些曲线上取点求和，如果取的点的和很大，那么代表着直线的斜率很大，同时也就意味着曲线的二次导数值较大。我们对一阶导数值的求和相当于对二阶导数值的采样，所以最佳步长确定为Adagrad的形式。

2.2 RMSProp

  根据Adagrad的分析我们可以知道，虽然它可以通过求和的方式来近似体现出二阶导数的特性，但是它到后期的速度往往会十分缓慢，因为他在一定程度上的对于过去的各个参数的重视程度是相当的；其次有的时候在神经网络中，待优化函数的形状可能是奇奇怪怪的，比如说对于同一个参数他的变化情况是不一样的，有的时候快，有的时候比较慢，如图所示

图6 .损失函数的曲线可能是一种十分复杂的形式

针对上面的那种情况，采用了如下的更新方法

上面的 α α 可以用来调节梯度，如果偏向于相信过去的梯度值应该选择较大的 α α ，如果偏向于相信现在的梯度值可以选择较小的 α α 值，这样即使遇到上面这种形状较为复杂的损失函数也可以根据调节 α α 值的来快速改变 w w 。
  其实RMSprop依然依赖于全局学习率；RMSprop算是Adagrad的一种发展，和Adadelta的变体，效果趋于二者之间，适合处理非平稳目标 - 对于RNN效果很好。

2.3 Adadelta

  Adadelta是对Adagrad的扩展，最初方案依然是对学习率进行自适应约束，但是进行了计算上的简化。 Adagrad会累加之前所有的梯度平方，而Adadelta只累加固定大小的项，并且也不直接存储这些项，仅仅是近似计算对应的平均值，即

⎧⎩⎨⎪⎪⎪⎪E|g2|t=ρE|g2|t−1+(1−ρ)g2tΔwt=−(√∑t−1r=1Δxr)(√E|g2|t)gt { E | g 2 | t = ρ E | g 2 | t − 1 + ( 1 − ρ ) g t 2 Δ w t = − ( ∑ r = 1 t − 1 Δ x r ) ( E | g 2 | t ) g t

其中因该注意的是使用的是过去梯度的均值，因此它的惯性并不是很大，所以不再使用全局的学习率。 这种方法训练初中期，加速效果不错，很快；训练后期，反复在局部最小值附近抖动。

3. 利用梯度变化信息

3.1 牛顿法（Hessian技术）

  牛顿法的基本思想是在现有极小点估计是的附近对 f(x) f ( x ) 做二阶泰勒展，进而找到极值点的下一个估计值。设 w0 w 0 是当前代价函数的极小点估计值，则

C(w0+Δw)=C(w0)+∑j∂C∂wjΔwj+12∑jkΔwj∂2C∂wj∂wkΔwk C ( w 0 + Δ w ) = C ( w 0 ) + ∑ j ∂ C ∂ w j Δ w j + 1 2 ∑ j k Δ w j ∂ 2 C ∂ w j ∂ w k Δ w k

可以将上述的等式丢弃更高阶的项压缩为

C(w0+Δw)=C(w0)+∇CΔw+12ΔwTHΔw C ( w 0 + Δ w ) = C ( w 0 ) + ∇ C Δ w + 1 2 Δ w T H Δ w

其中 ∇C ∇ C 是通常的梯度向量， H H 就是矩阵形式的 Hessian 矩阵，其中第 jk j k 项就是 ∂2C∂wj∂wk ∂ 2 C ∂ w j ∂ w k 。由极值条件必要条件可知， C′(w0+Δw) C ′ ( w 0 + Δ w ) 应满足

C′(w0+Δw)=0 C ′ ( w 0 + Δ w ) = 0

因此对上式两侧求导可得

C′(w0+Δw)=∇C+HΔw=0 C ′ ( w 0 + Δ w ) = ∇ C + H Δ w = 0

如果海森矩阵是正定的，则

Δw=−H−1∇C Δ w = − H − 1 ∇ C

  因此利用牛顿法进行迭代的过程就是

• 1 选择开始点 w0 w 0 ；
• 2 更新 w0 w 0 到新点 w1=w0−H−1∇C w 1 = w 0 − H − 1 ∇ C ，其中的 H H 和 ∇C ∇ C 是在 w0 w 0 处计算出来的；
• 3 更新 w1 w 1 到新点 w2=w1−H−1∇C w 2 = w 1 − H − 1 ∇ C ，其中的 H H 和 ∇C ∇ C 是在 w1 w 1 处计算出来的。

  在理论上和实践中的结果都表明 Hessian 方法比标准的梯度下降方法收敛速度更快。特别地，通过引入代价函数的二阶变化信息，可以让 Hessian 方法避免在梯度下降中常碰到的多路径（pathologies）问题。
  但是牛顿法也有三个无法规避的缺点，首先它没有步长因子，而是定步长迭代，对于非二次型目标函数，有时函数值会上升，因此牛顿法不能保持函数值稳定的下降；其次对目标函数由较为严格的要求，函数必须具有连续的一、二阶偏导数，海森矩阵必须为正定；第三计算相当复杂，除了计算梯度以外，还需要计算二阶偏导数矩阵和它的逆矩阵。

3.2 基于Momentum的梯度下降

  在上一小节中，Hessian 优化的优点是它不仅仅考虑了梯度，而且还包含梯度如何变化的信息；但是也同样具有没有步长因子、对目标函数要求严格和计算相当复杂的缺点。根据这些特点，研究人员提出了基于Momentum的梯度下降方法，如图让我们回顾一下梯度下降的过程

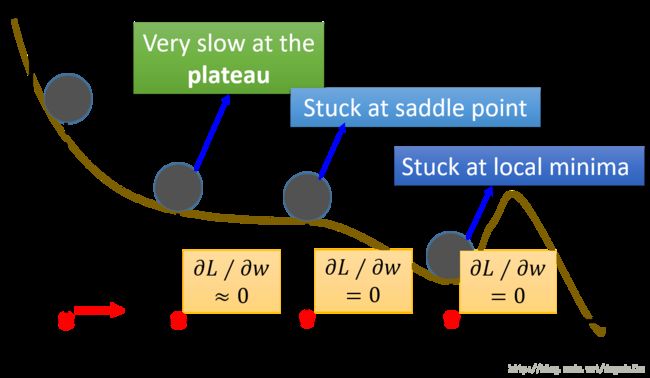
图7 . 梯度下降过程中如用停止的地方

如上图所示，横坐标是是神经网络参数 w w 的值，纵坐标是总体损失的值，从图中可以看到，在梯度下降的过程中，参数在高原（Plateau）上具有十分缓慢的参数更新速率，在鞍点会停止参数更新，或者陷入一个局部最小值（关于局部最小值还有一个补充说明，就是有一种理论认为在神经网络的代价函数中并没有太多的局部最小值，这只因为如果一个点处于局部最小值的话，那么这个点在它的每一个维度都处于局部最小值，这样的概率是很小的，因此在实际的训练中没有想象中那么多的局部最小值）。我们常常将梯度学习的过程比做是一个小球像谷底滚落的过程，因此在小球滚落的过程中如果可以使小球具有惯性，就有可能克服上面三种情况 。
  momentum 技术修改了梯度下降的两处使之类似于这个物理场景。

• 1 首先，为我们想要优化的参数引入了一个称为速度（velocity）的概念。梯度的作用就是改变速度，而不是直接的改变位置，就如同物理学中的力改变速度，只会间接地影响位置；同样速度在这个过程中也会叠加，进而得到类似于惯性的表现。
• 2 第二，momentum 方法引入了一种摩擦力的项，用来逐步地减少速度。

  具体的数学描述为：引入速度变量 v=v1,v2,... v = v 1 , v 2 , . . . ，并取初始值 v=0 v = 0 。其中每一个分量对应 wj w j 变量 （在一个神经网络中，变量 wj w j 当然也包括所有的权重和偏置），则此时的梯度下降更新规则为

{v→v′=μv−η∇Cw→w′=w+v′ { v → v ′ = μ v − η ∇ C w → w ′ = w + v ′

首先介绍其中的超参数 μ μ ，它叫做 moment coefficient， 是用来控制阻碍或者摩擦力的量的超参数，准确地说，你应该将 1−μ 1 − μ 看成是摩擦力的量。当 μ=1 μ = 1 时，没有摩擦，速度完全由梯度决定（实际是以往所有梯度的累加和），梯度下降运行得更快，有时达到谷底，可能会跨越过去；或者，梯度本该快速改变，但是因为之前的惯性过大而没有改变。相反当 μ=0 μ = 0 时，，就存在很大的摩擦，速度无法叠加，上述公式就变成了通常的梯度下降 。在实践中，使用 0 和 1 之间的值可以给带来叠加速度的好处又避免速度过量。我们可以使用 hold out 验证数据集来选择合适的 μ μ 值，就像我们之前选择 η η 和 λ λ 那样。
  其中速度的累加体现在 v→v′=μv−η∇C v → v ′ = μ v − η ∇ C ，将速度按这个公式迭代下去可以很明显看到速度实际上在叠加过去所用过的梯度值，而累加的程度由超参数 μ μ 控制。下面我们同图像上进行一个直观的理解

图8 .momentum迭代过程示意图

在上图中，红色的方向为计算出的梯度方向，蓝色方向是参数实际移动的方向，绿色方向是参数上一次移动的方向，所以参数每一次移动的方向都是与上一次移动的方向以及现在的梯度方向相关。如果将这个过程在代价函数曲线上演示，则如下图所示

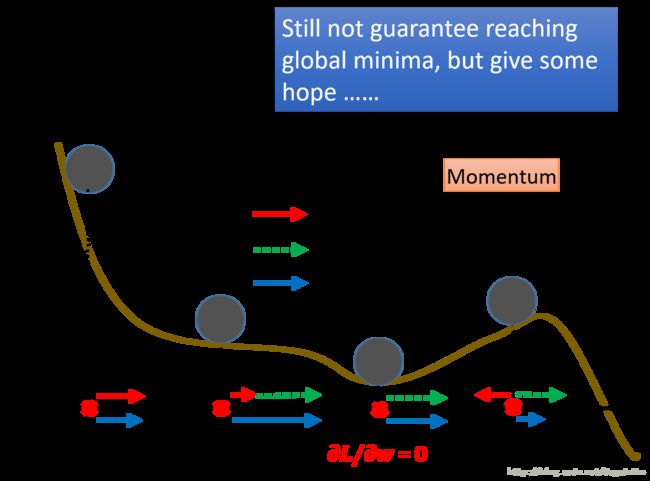
图9 .momentum在代价函数曲线上迭代过程示意图

在上图中，三种颜色的线所代表的含义与上上图中的含义相同。我们可以看到，在高原部分，迭代过程可能凭借之前的速度，令其在这部分参数更新的速度得以增加；在鞍点部分，同样能凭借之前的速度跨过鞍点；最后在局部最小值中，也可能凭借之前的速度跨过。所以基于Momentum的梯度下降虽然不能保证得到一个全局最小值，但是至少给了我们可能性。
  基于Momentum的梯度下降的主要优点在于四点：首先他的迭代形式简单，不需要改变过多的梯度下降算法便可以实现，且仍然可以利用反向传播计算公式；其次利用了梯度信息，但是避免了hessian矩阵的求取降低了计算更复杂度；利用速度的累加，提供了避免函数陷于高原、鞍点以及局部最小值的可能性；最后是这种方法带来了学习速度的提升。
  同样这种方法也有着自身的两个缺点：首先容易跨过全局最小点，其次可能因为惯性过大造成在应该改变梯度（主要指的是下降方向）时无法及时改变。

3.3 NAG

  Nesterov accelerated gradient(NAG,涅斯捷罗夫梯度加速)不仅增加了动量项，并且在计算参数的梯度时，在损失函数中减去了动量项，即计算

⎧⎩⎨⎪⎪⎪⎪⎪⎪gt=∇C(wt−1−vt−1)vt=μvt−1−ηgtwt+1=wt+vt { g t = ∇ C ( w t − 1 − v t − 1 ) v t = μ v t − 1 − η g t w t + 1 = w t + v t

这种方式首先预估了下一次参数所在的位置，再加上动量项，这样可以阻止过快更新来提高响应性。NAG可以看作是Momentum的改进版，两者主要的区别如下图所示

图10 .NAG与Momentum的主要区别示意图

从图中可以明显看到，Momentum下一步的方向由过去的动量以及现在的梯度值决定；而NAG根据过去的动量以及预测由动量带来的下一步的梯度决定。

4. Adam

挖个坑，具体细节日后来填

5. 总体分析

  下面两幅图可视化形象地比较上述各优化方法

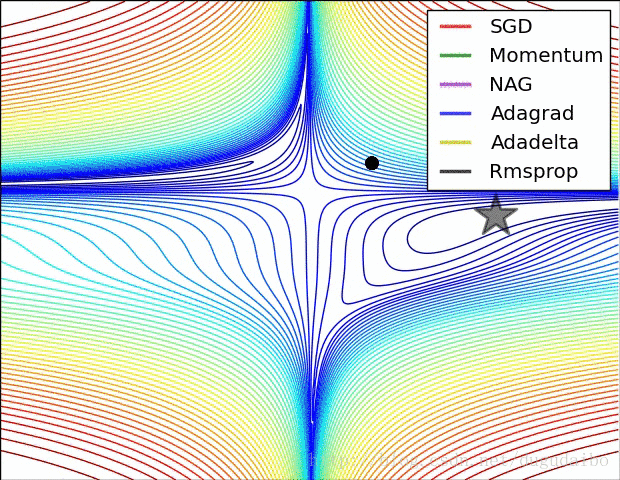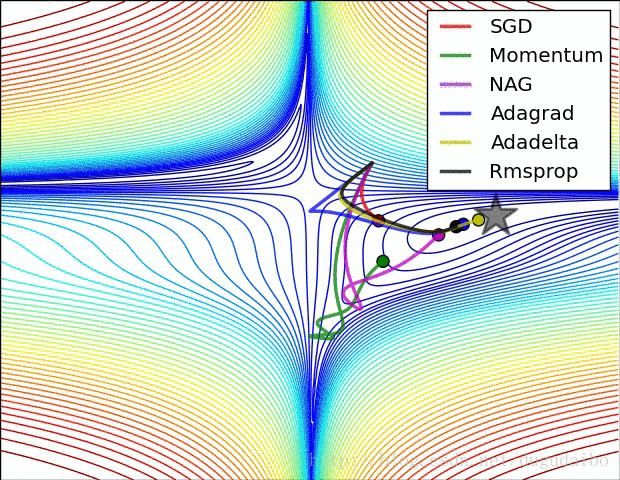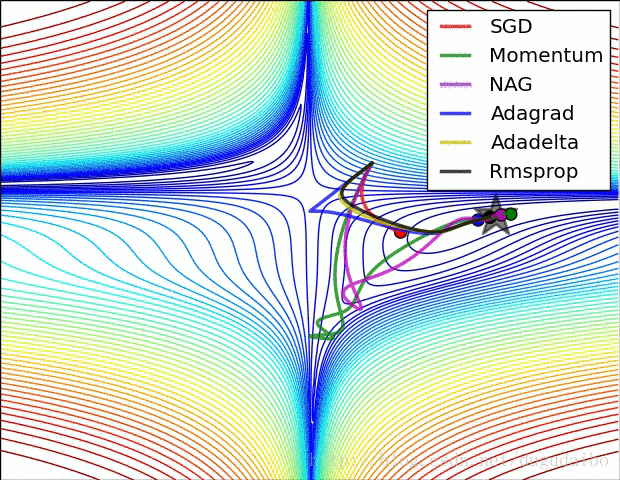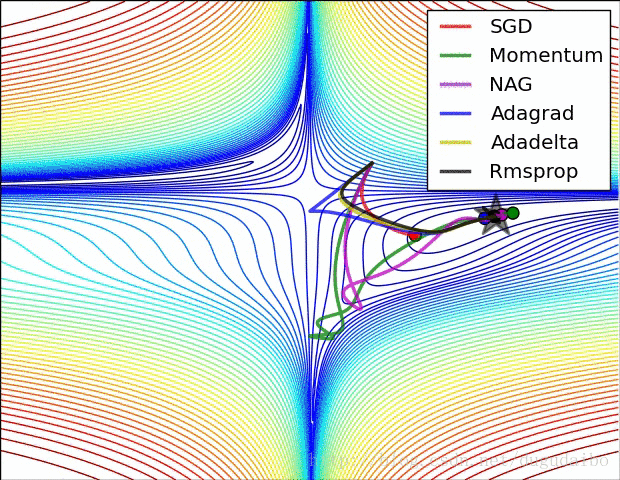
图11 . 上述各种梯度下降算法效果对比图

从上图中左图可以看出， Adagrad、Adadelta与RMSprop在损失曲面上能够立即转移到正确的移动方向上达到快速的收敛。而Momentum 与NAG会导致偏离(off-track)。同时NAG能够在偏离之后快速修正其路线，因为其根据梯度修正来提高响应性。从上图右图可以看出，在鞍点（saddle points）处(即某些维度上梯度为零，某些维度上梯度不为零)，SGD、Momentum与NAG一直在鞍点梯度为零的方向上振荡，很难打破鞍点位置的对称性；Adagrad、RMSprop与Adadelta能够很快地向梯度不为零的方向上转移。
   从上面两幅图可以看出，自适应学习速率方法(Adagrad、Adadelta、RMSprop与Adam)在这些场景下具有更好的收敛速度与收敛性。RMSprop是Adagrad的一种扩展，与Adadelta类似，但是改进版的Adadelta使用RMS去自动更新学习速率，并且不需要设置初始学习速率。而Adam是在RMSprop基础上使用动量与偏差修正。RMSprop、Adadelta与Adam在类似的情形下的表现差不多。Kingma指出收益于偏差修正，Adam略优于RMSprop，因为其在接近收敛时梯度变得更加稀疏。因此，Adam可能是目前最好的SGD优化方法。