傅里叶级数推导
物理意义:把一个比较复杂的周期运动看成是许多不同频率的简谐振动的叠加。
三角函数系
cos x, sinx, cos2x, sin2x.…, cosnx, sinnx.…
正交性
在[- π \pi π, π \pi π]上正交,即其中任意两个不同的函数之积在[- π \pi π, π \pi π]上的积分等于0.
可以证明:
- ∫ − π π cos n x d x = 0 \int_{-\pi}^{\pi} \cos n x d x=0 ∫−ππcosnxdx=0
- ∫ − π π sin n x d x = 0 \int_{-\pi}^{\pi} \sin n x d x=0 ∫−ππsinnxdx=0
- ∫ − π π cos m x cos n x d x = 0 ( m = 1 , 2 , 3 , ⋯ , n = 1 , 2 , 3 , ⋯ m ≠ n ) \begin{array}{c}{\int_{-\pi}^{\pi} \cos m x \cos n x d x=0 \quad(m=1,2,3, \cdots, n=1,2,3, \cdots m \neq n )}\end{array} ∫−ππcosmxcosnxdx=0(m=1,2,3,⋯,n=1,2,3,⋯m̸=n)
- ∫ − π π sin m x sin n x d x = 0 ( m = 1 , 2 , 3 , ⋯ , n = 1 , 2 , 3 , ⋯ m ≠ n ) \begin{array}{c}{\int_{-\pi}^{\pi} \sin m x \sin n x d x=0 \quad(m=1,2,3, \cdots, n=1,2,3, \cdots m \neq n )}\end{array} ∫−ππsinmxsinnxdx=0(m=1,2,3,⋯,n=1,2,3,⋯m̸=n)
- ∫ − π π sin m x cos n x d x = 0 ( m = 1 , 2 , 3 , ⋯ , n = 1 , 2 , 3 , ⋯ ) \begin{aligned} \int_{-\pi}^{\pi} \sin m x \cos n x d x &=0 \quad(m=1,2,3, \cdots, n=1,2,3, \cdots ) \end{aligned} ∫−ππsinmxcosnxdx=0(m=1,2,3,⋯,n=1,2,3,⋯)当m=n时
∫ − π π 1 ⋅ 1 d x = 2 π ∫ − π π cos 2 n x d x = π ∫ − π π sin 2 n x d x = π ( n = 1 , 2 , ⋯ ) \begin{array}{l}{\int_{-\pi}^{\pi} 1 \cdot 1 \mathrm{d} x=2 \pi} \\\\ {\int_{-\pi}^{\pi} \cos ^{2} n x d x=\pi} \\\\ {\int_{-\pi}^{\pi} \sin ^{2} n x d x=\pi}\end{array}(n=1,2, \cdots) ∫−ππ1⋅1dx=2π∫−ππcos2nxdx=π∫−ππsin2nxdx=π(n=1,2,⋯)
设 f ( x ) f(x) f(x)是周期为2 π \pi π的周期函数,且可逐项积分,利用三角级数得
f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n x + b n sin n x ) f(x)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left(a_{n} \cos n x+b_{n} \sin n x\right) f(x)=2a0+n=1∑∞(ancosnx+bnsinnx) 想要表达 f ( x ) f(x) f(x)得求出 a 0 , a n , b n a_{0},a_{n},b_{n} a0,an,bn,对两边进行积分得
∫ − π π f ( x ) d x = ∫ − π π a 0 2 d x + ∑ n = 1 ∞ [ ∫ − π π a n cos n x d x + ∫ − π π b n sin n x d x ] \begin{aligned} \int_{-\pi}^{\pi} f(x) \mathrm{d} x=& \int_{-\pi}^{\pi} \frac{a_{0}}{2} \mathrm{d} x+\sum_{n=1}^{\infty}\left[\int_{-\pi}^{\pi} a_{n} \cos n x \mathrm{d} x\right. +\int_{-\pi}^{\pi} b_{n} \sin n x \mathrm{d} x ] \end{aligned} ∫−ππf(x)dx=∫−ππ2a0dx+n=1∑∞[∫−ππancosnxdx+∫−ππbnsinnxdx]因为 a 0 , a n , b n a_{0}, a_{n}, b_{n} a0,an,bn为常数,利用三角函数的正交性 - ∫ − π π cos n x d x = 0 \int_{-\pi}^{\pi} \cos n x d x=0 ∫−ππcosnxdx=0
- ∫ − π π sin n x d x = 0 \int_{-\pi}^{\pi} \sin n x d x=0 ∫−ππsinnxdx=0
得到
∫ − π π f ( x ) d x = ∫ − π π a 0 2 d x = π a 0 \int_{-\pi}^{\pi} f(x) \mathrm{d} x=\int_{-\pi}^{\pi} \frac{a_{0}}{2} \mathrm{d} x=\pi a_{0} ∫−ππf(x)dx=∫−ππ2a0dx=πa0
a 0 = 1 π ∫ − π π f ( x ) d x a_{0}=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) d x a0=π1∫−ππf(x)dx
为了求 a n a_{n} an,在等式两边 cos k x \cos k x coskx
∫ − π π f ( x ) cos k x d x = ∫ − π π a 0 2 cos k x d x + ∑ n = 1 ∞ I − π π a n cos k x cos n x d x + ∫ − π π b n cos k x sin n x d x ] \begin{aligned} \int_{-\pi}^{\pi} f(x) \cos k x d x &=\int_{-\pi}^{\pi} \frac{a_{0}}{2} \cos k x d x \\ &+\sum_{n=1}^{\infty} I_{-\pi}^{\pi} a_{n} \cos k x \cos n x d x \\ &+\int_{-\pi}^{\pi} b_{n} \cos k x \sin n x d x ] \end{aligned} ∫−ππf(x)coskxdx=∫−ππ2a0coskxdx+n=1∑∞I−ππancoskxcosnxdx+∫−ππbncoskxsinnxdx]当k=n时,由三角函数的正交性可知 ∫ − π π a n cos k x cos n x d x = ∫ − π π a n cos 2 n x d x = a n ∫ − π π 1 + cos 2 n x 2 d x = a n π \begin{aligned} & \int_{-\pi}^{\pi} a_{n} \cos k x \cos n x d x=\int_{-\pi}^{\pi} a_{n} \cos ^{2} n x d x \\=& a_{n} \int_{-\pi}^{\pi} \frac{1+\cos 2 n x}{2} d x=a_{n} \pi \end{aligned} =∫−ππancoskxcosnxdx=∫−ππancos2nxdxan∫−ππ21+cos2nxdx=anπ其余各项均为零.因此 a n = 1 π ∫ − π π f ( x ) cos n x d x ( n = 1 , 2 , 3 , ⋯ ) a_{n}=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos n x d x \quad(n=1,2,3, \cdots) an=π1∫−ππf(x)cosnxdx(n=1,2,3,⋯)同理 b n = 1 π ∫ − π π f ( x ) sin n x d x ( n = 1 , 2 , 3 , ⋯ ) b_{n}=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin n x d x \quad(n=1,2,3, \cdots) bn=π1∫−ππf(x)sinnxdx(n=1,2,3,⋯)
整理一下得:
{ a n = 1 π ∫ − π π f ( x ) cos n x d x ( n = 0 , 1 , 2 , ⋯ ) b n = 1 π ∫ − π π f ( x ) sin n x d x ( n = 1 , 2 , 3 , ⋯ ) \left\{\begin{array}{ll}{a_{n}=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos n x d x} & {(n=0,1,2, \cdots)} &\\\\ {b_{n}=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin n x d x} & {(n=1,2,3, \cdots)}\end{array}\right. ⎩⎨⎧an=π1∫−ππf(x)cosnxdxbn=π1∫−ππf(x)sinnxdx(n=0,1,2,⋯)(n=1,2,3,⋯)
a n ( 0 开 始 的 ) , b n a_{n}(0开始的),b_{n} an(0开始的),bn称为傅里叶系数。由傅里叶系数组成的三角级数称为傅里叶级数。
例
f ( x ) = { − 1 , − π ≤ x < 0 1 , 0 ≤ x < π f(x)=\left\{\begin{array}{lr}{-1,} & {-\pi \leq x<0} \\ {1,} & {0 \leq x<\pi}\end{array}\right. f(x)={−1,1,−π≤x<00≤x<π
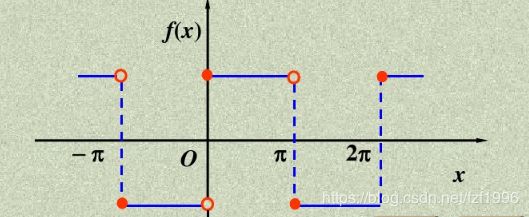
a n = 1 π ∫ − π π f ( x ) cos n x d x = 1 π ∫ − π 0 ( − 1 ) cos n x d x + 1 π ∫ 0 π cos n x d x = − 1 π 1 n sin n x ] − π 0 + 1 π 1 n sin n x ] 0 π = 0 ( n = 0 , 1 , 2 , 3 ⋯ ) \begin{aligned} a_{n} &=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \cos n x d x \\ &=\frac{1}{\pi} \int_{-\pi}^{0}(-1) \cos n x d x+\frac{1}{\pi} \int_{0}^{\pi} \cos n x d x \\ &=-\frac{1}{\pi} \frac{1}{n} \sin n x ]_{-\pi}^{0}+\frac{1}{\pi} \frac{1}{n} \sin n x ]_{0}^{\pi}=0 \\ &(n=0,1,2,3 \cdots) \end{aligned} an=π1∫−ππf(x)cosnxdx=π1∫−π0(−1)cosnxdx+π1∫0πcosnxdx=−π1n1sinnx]−π0+π1n1sinnx]0π=0(n=0,1,2,3⋯)
b n = 1 π ∫ − π π f ( x ) sin u x d x = 1 π ∫ − π 0 ( − 1 ) sin x d x + 1 π ∫ 0 π sin x d x = 1 π 1 n cos n x ∣ − π 0 − 1 π [ 1 n cos n x ] 0 π = 2 n π [ 1 − ( − 1 ) n ] = { 4 n π , n = 1 , 3 , 5 , ⋯ 0 \begin{aligned} b_{n} &=\frac{1}{\pi} \int_{-\pi}^{\pi} f(x) \sin u x d x \\ &=\frac{1}{\pi} \int_{-\pi}^{0}(-1) \sin x d x+\frac{1}{\pi} \int_{0}^{\pi} \sin x d x \\ &=\frac{1}{\pi} \frac{1}{n} \cos n\left.x\right|_{-\pi} ^{0}-\frac{1}{\pi}\left[\frac{1}{n} \cos n x\right]_{0}^{\pi} \\ &=\frac{2}{n \pi}\left[1-(-1)^{n}\right] \\ &=\left\{\begin{array}{l}{\frac{4}{n \pi}, n=1,3,5, \cdots} \\ {0}\end{array}\right. \end{aligned} bn=π1∫−ππf(x)sinuxdx=π1∫−π0(−1)sinxdx+π1∫0πsinxdx=π1n1cosnx∣−π0−π1[n1cosnx]0π=nπ2[1−(−1)n]={nπ4,n=1,3,5,⋯0所以 f ( x ) = ∑ n = 1 ∞ b n sin n x = 4 π [ sin x + 1 3 sin 3 x + ⋯ + 1 2 n − 1 sin ( 2 n − 1 ) x + ⋯ ] f(x)=\sum_{n=1}^{\infty}b_{n} \sin n x\\=\frac{4}{\pi}\left[\sin x+\frac{1}{3} \sin 3 x+\cdots+\frac{1}{2 n-1} \sin (2 n-1) x+\cdots\right] f(x)=n=1∑∞bnsinnx=π4[sinx+31sin3x+⋯+2n−11sin(2n−1)x+⋯]