【机器学习笔记】——模型评价准则（Evaluation metrics）

目 录

1 模型选择

  模型选择有两个思路，一是解释性。即在现有数据下哪些特征是重要的特征，应该用什么样的模型来解释数据。好的模型应该是最能解释现有数据的模型，也就是说更能拟合训练集数据的模型（训练误差小）。二是预测性，好的模型应该是泛化能力更强的模型，也就是说在测试集上表现更好的模型。笔记里主要关注的是后者，即如何评价一个训练好了的模型（已知参数的模型）的好坏

2 回归任务

2.1 MSE（Mean Square Error）均方误差

$$MSE=\frac{1}{N}\sum _{i=1}^N{(y_i-\widehat{y_i})}^2\text{\hspace{1em}(1)}$$

  在训练模型时常被用作线性回归的损失函数，所以自然地也拿来在测试集上评价模型

2.2 RMSE（Root Mean Square Error）均方根误差

$$RMSE=\sqrt{MSE}=\sqrt{\frac{1}{N}\sum _{i=1}^N{(y_i-\widehat{y_i})}^2}\text{\hspace{1em}(2)}$$

  常作为机器学习模型预测结果的评价准则，比如随机森林回归和XGBregressor的默认评价准则都是这个。RMSE和MSE的区别仅在于做了一个平方，使得量纲和变量保持一致，有点像平方差和标准差的感觉。所以对于评价模型两者没什么优劣之分，只不过RMSE可能有更好的解释性。

2.3 RMSLE（Root Mean Square Log Error）均方根对数误差

$$RMSLE=\sqrt{\frac{1}{N}\sum _{i=1}^N{(\log (y_i+1)-\log (\widehat{y_i}+1))}^2}\text{\hspace{1em}(3)}$$

  使用RMSLE的好处：

•   一个有趣的现象是使用RMSLE对于预测值较小的惩罚更大：考虑只有一个实例的学习，如果真实值为1000，预测值为1100，此时 $RMSE=100$，$RMSLE=0.095$；如果预测值为900，此时 $RMSE=100$，$RMSLE=0.105$。这一点可能对于特殊的情况有一些好处

•   取对数是一个变化量纲的变换，能够把一些大的值压缩，把一些小的值增大。所以当数据中有少量的值和真实值差别较大时，RMSLE能够降低这些值对于整体误差的影响，这会降低个别异常点对于模型评价的影响。

•   同前一条有点类似，如果要预测的数据的量纲很大，比如一个左偏的模型。那么如果模型在大的真实值处的误差就会使RMSE的结果很大，得出这个模型不好的结论；而如果一个事实上很差的模型在这个大的真实值上的预测很准确而在非常多的小的真实值处有一些误差，那么的RMSE反而会没有前面那个模型的大，得出这个模型更好的结论。RMSLE就是会降低这种错误的准则。另一个方法是先对标签取 $\log$，再用RMSE作为评价准则，这需要提前认识数据的分布。

2.4 MAE（Mean Absolute Error）平均绝对误差

$$MAE=\frac{1}{N}\sum _{i=1}^N|y_i-\widehat{y_i}|\text{\hspace{1em}(4)}$$

  因为这个函数不是处处可导，所以没有用作线性回归训练模型的损失函数，但是这不影响它可以作为测试集上的模型评价准则。MAE和RMSE具有同样的量纲，但是RMSE会对误差平方后再求和，也就是说它能够放大误差更大的样本的影响，而MAE就是真实误差的直接反映。RMSE越小说明最大误差越小，因为能反映最大误差，所以RMSE更常用一些。

2.5 $R^2$（R Squared）R方

$$R^2=1-\frac{SSR}{SST}=1-\frac{{\sum }_{i=1}^N{(y_i-\widehat{y_i})}^2}{{\sum }_{i=1}^N{(y_i-\overline{y_i})}^2}=1-\frac{MSE}{Var}\text{\hspace{1em}(5)}$$

  R方是线性回归中非常常用的评价准则，先来了解一下R方的产生。我们先以RMSE为例，对于同一个预测身高的模型，如果把标签的单位从米换成厘米，那么RMSE就会变成原来的100倍，那么能不能说用米做单位的模型更好呢，这显然说不通，因为两个模型是等价的。一个自然的想法是，既然RMSE研究的是数据的绝对误差，那么只要用相对误差就好了，那么相对于什么呢？考虑先相对于原始数据的平方和

$$\frac{{\sum }_{i=1}^N{(y_i-\widehat{y_i})}^2}{{\sum }_{i=1}^N{y_i}^2}\text{\hspace{1em}(6)}$$

  这样看似是不错的，但是仍然存在一些问题，就是如果 $Y$ 增加平移，结果就会产生变化。比如我们希望研究的是相对于海平面的身高而不是相对于地面的身高，那么所有的真实值和预测值都会加上一个所在地面的海拔高度。这样一来分子并不会因为这一段海拔高度变化，而分母却会产生变化。我们真正关心的是不同的人身高之间的差异与哪些因素有关，只是改变了测量身高的参考系，不应该改变模型对不同的人身高差异的预测能力，所以上面采用误差平方和与真实值比值的评分方式也需要改进。

  为了使得我们的模型好坏评分系统不会因为模型里的预测值同时增加会减小一个固定值（比如像上面的例子那样将参考系从地面变成海平面）而改变，可以先将 $Y$ 的预测值先减去其平均值（这一过程也叫做中心化），再取平方和，叫做总平方和

$$\frac{{\sum }_{i=1}^N{(y_i-\widehat{y_i})}^2}{{\sum }_{i=1}^N{(y_i-\overline{y_i})}^2}\text{\hspace{1em}(7)}$$

  我们也把分母表示的模型称为基准模型，即把平均值作为真实值的预测。到了这里我们就已经得到了一个不错的评价准则，但是在我们的惯性思维中一般都是评分高，结果越好，所以我们用 1 减去上面的分式作为最终结果，也就是R方。

$$R^2=1-\frac{{\sum }_{i=1}^N{(y_i-\widehat{y_i})}^2}{{\sum }_{i=1}^N{(y_i-\overline{y_i})}^2}\text{\hspace{1em}(8)}$$

  所以R方的一个好处是不会随着预测值单位的变化而变化，也不会因为预测值的平移而变化。

  从上面我们知道R方越大，模型越好。当我们的预测完全正确时，那么R方等于最大值 1，当我们使用基准模型预测（预测值等于真实值的平均值）时，R方为0。因此R方的另一个好处就是将回归结果归约到了0~1间，允许我们对不同问题的预测结果进行比对（当然有时候R方也会出现小于0的情况）。

2.5.1 R方小于0？R方大于1？

  我们知道 $SST=SSR+SSE$，而且这三个平方和都是正的，那么一定有 $SST\ge SSR$，那么为什么会出现R方小于0呢？这是因为 $SST=SSR+SSE$ 成立是需要条件的，即回归方程有截距。先看一下方差的分解式

$$\begin{array}{rl}SST& =\sum {(y_i-\bar{y})}^2\\ & =\sum {\left((y_i-\widehat{y_i})-(\bar{y}-\widehat{y_i})\right)}^2\\ & =\sum {(y_i-\widehat{y_i})}^2+\sum (\bar{y}-\widehat{y_i})-2\sum (y_i-\widehat{y_i})(\bar{y}-\widehat{y_i})\\ & =SSR+SSE-2\bar{y}\sum (y_i-\widehat{y_i})+2\sum \widehat{y_i}(y_i-\widehat{y_i})\end{array}$$

  在有截距项的假设下：$Y={\beta }_0+{\beta }_{1}X$，我们要使SSR最小，于是让SSR分别对 ${\beta }_0$、${\beta }_1$ 求偏导得到：

$$\frac{\partial SSR}{\partial {\beta }_0}=\frac{\partial \sum {(y_i-\widehat{y_i})}^2}{\partial {\beta }_0}=-2\sum (y_i-\widehat{y_i})\frac{\partial y_i}{\partial {\beta }_0}=-2\sum (y_i-\widehat{y_i})=0\text{\hspace{1em}(10)}$$

$$\frac{\partial SSR}{\partial {\beta }_1}=\frac{\partial \sum {(y_i-\widehat{y_i})}^2}{\partial {\beta }_1}=-2\sum (y_i-\widehat{y_i})\frac{\partial y_i}{\partial {\beta }_1}=-2\sum (y_i-\widehat{y_i})x_i=0\text{\hspace{1em}(11)}$$

  由(10)和(11)式以及 $y_i={\beta }_0+{\beta }_1{x}_i$ 得出方差分解式的后两项都是0，于是才有 $SST=SSR+SSE$。

  如果没有截距项，还是求偏导只能得到(11)式的结果，于是

$$SST=SSR+SSE-2\bar{y}\sum (y_i-\widehat{y_i})\text{\hspace{1em}(12)}$$

  所以当 $SSE-2\bar{y}\sum (y_i-\widehat{y_i})<0$ 时，$SSR>SST$，就有了R方小于0。同样的道理，当 $SSE-2\bar{y}\sum (y_i-\widehat{y_i})<0$ 时，就会有R方大于 1。 总之只要我们的回归方程是有截距项的，那么R方一定在 0 和 1 之间。

2.5.2 adjusted $R^2$ （adjusted R squared）调整后的R方

  如果一个自变量对减小误差平方和完全没有帮助，则线性模型会自动放弃使用这一自变量，将它的回归系数设为 0。这也就是说，往模型里面加入新的自变量，模型的误差平方和只会减小不会增加，从而 R方 只会增加不会减小。这就使得用 R方 来比较包含不同数量的自变量的模型时候，总会对自变量多的模型比较偏心，这有时候并不合理。于是我们对增加变量进行惩罚，禁止随意的增加非显著变量

$$R_{adjusted}^2=1-\frac{SSR/(n-p-1)}{SST/(n-1)}\text{\hspace{1em}(13)}$$

3 分类任务

3.1 error & accuracy（ACC） 错误率和准确率

  很直观易懂，错误率就是错误样本数比上总样本数，准确率就是正确样本数比上总样本数。对于多分类问题也是这样。这是分类任务最直接有效的评价准则。

3.2 logloss

  又称为逻辑损失（logistic regression loss）或者交叉熵损失（cross-entropy loss）。他根据给出每个实例对应的标签的概率给出一个值作为标准，比如对于二分类任务，模型判断一个实例的标签为真实值 $y$ 和它预测为真实值为 1 的概率 $p$，于是logloss定义为

$$-\log (y/p)=-\left(y\log (p)+(1-y)\log (1-p)\right)\text{\hspace{1em}(14)}$$

推广到多分类任务

$$-\log (Y/P)=-\frac{1}{N}\sum _{i=1}^N\sum _{k=1}^K{y}_{i,k}\log p_{i,k}\text{\hspace{1em}(15)}$$

3.3 AUC & AUCPR & KS

  准确率是一个很好的评价指标了，那么为什么需要AUC等其他指标呢？加入一个数据中99%的样本是正例，只有1%的样本是负例，那么我们什么都不做，把所有样本预测为正例就可以。而AUC能够保证在样本不均衡的情况下也能准确评估模型的好坏，而K-S值不仅能告诉模型准确与否，还能告诉模型对正负样本是否有足够高的区分度

3.3.1 混淆矩阵

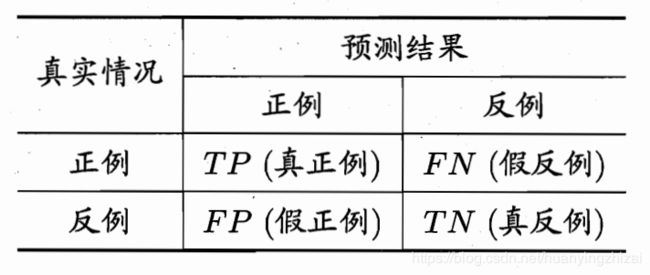
  对于二分类问题我们可以根据预测结果和样本的真实情况分为四种组合，表示在矩阵中就是混淆矩阵。下图所示即为混淆矩阵

从混淆矩阵中我们可以得到一些有用的评价准则：

3.3.2 查准率、查全率、P-R曲线、AUCPR、F值

3.3.2.1 查全率

  Recall（召回率/查全率），又称为sensitivity（灵敏度）或者 true positive rate（真正例率，TPR）。反映了被正确预测的正例样本在所有正例样本中的比例，在特殊的任务中该指标比错误率或者准确率更好，比如在地震预测中我们不在乎所有预报中预测成功的准确率是多少，而是在所有的地震中，我们能正确预测出多少次，即求全而不求准

$$Recall=\frac{TP}{TP+FN}\text{\hspace{1em}(16)}$$

3.3.2.2 查准率

  Precision（精准率/查准率），又称为Positive predictive value (PPV)。反映了被预测为正例的样本中真正为正例的比重，这个指标也适用于特殊的分类任务，比如在用人脸识别抓捕逃犯时，我们希望不冤枉一个好人不放过一个坏人，那么就要求被识别为逃犯的人是真的逃犯才行，即求准而不求全。

$$Precision=\frac{TP}{TP+FP}\text{\hspace{1em}(17)}$$

  为了增大求全率，我们就需要扩大预测为正例样本的数量，这会牺牲查准率，而为了增大查准率，我们需要尽可能减少我们不特别确定是正例的样本，这就会漏掉一些真正是正例的样本，牺牲了查全率，所以这两个指标是一对矛盾的度量。通常只有在样本量较小的简单任务中两者才会都比较高。

3.3.2.3 P-R曲线 & AUCPR & F值

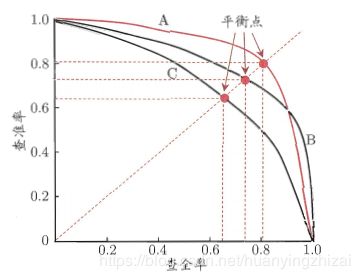
  把样本按照学习器认为是正例的概率从大到小进行排序，按此顺序逐个把样本作为正例进行预测（比如第一次第一个视为正例，剩余的视为反例，第二次前两个视为正例，剩余的视为反例。这样查全率从0到1查准率从1到0变化），那么每次可以得到当前的查准率和查全率，以查准率为纵轴，查全率为横轴，就得到了查准率-查全率曲线，即“P-R曲线”。因为这个概率是学习器学得的，所以每个学习器都能画出一条P-R曲线。

  根据P-R图比较学习器的性能时，认为包在外面（这里的外指的是右上角）的曲线性能更好（查准率、查全率都更高），比如学习器B优于学习器C。当出现P-R曲线相交的情况时，一般需要根据具体情况判断学习器的好坏，或者比较两个曲线下方的面积AUCPR（Area under the PR Curve），下方面积更大的曲线对应的学习器好。但是这个值并不容易估算，所以又引入了另一个性能度量——“平衡点”。它是曲线与 $y=x$ 的交点，即查准率等于查全率，并认为平衡点更高的曲线对应的学习器性能更好，依次判断学习器A优于学习器B。

  另一个更常用的评价标准是F值

$$F_1=2\times \frac{Precision\cdot Recall}{Precision+Recall}\text{\hspace{1em}(18)}$$

F值更高的学习器性能更好。

  有时候任务对查全率和查准率的偏好不同，这时候引入F值的一般形式

$$F_{\beta }=(1+{\beta }^2)\times \frac{Precision\cdot Recall}{{\beta }^2\times Precision+Recall}\text{\hspace{1em}(19)}$$

其中 $\beta >0$ 度量了查全率对查准率的相对重要性，$\beta >1$ 时更关注查全率，$\beta <1$ 时更关注查准率

3.3.3 真正例率、假正例率、ROC曲线、AUC

3.3.3.1 真正例率

  真正例率是前面查全率的别称，反映了被正确预测的正例样本在所有正例样本的比重

3.3.3.2 假正例率

  False Positive Rate（假正例率），反映了实际为负例但被预测为正例的样本在所有负例样本中的比重

$$FPR=\frac{FP}{FP+TN}\text{\hspace{1em}(20)}$$

3.3.3.3 ROC曲线

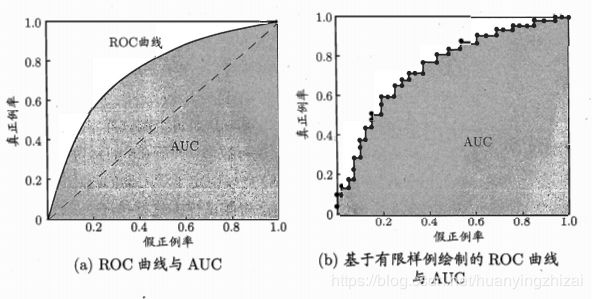
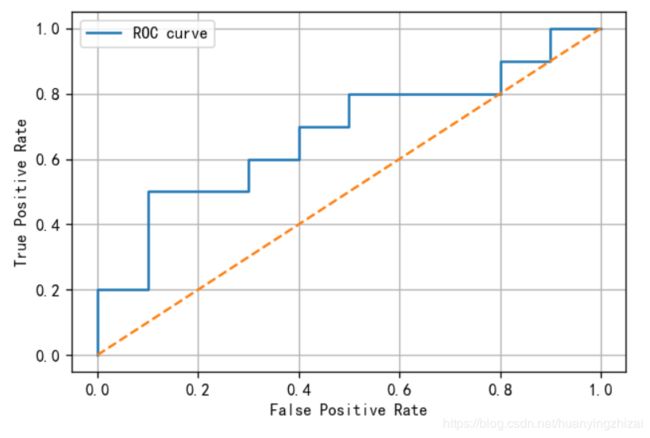
  按照画P-R曲线的方式先对样本进行排序，每次计算真正例率和假正例率作为纵轴和横轴，画出的就是ROC曲线（Receiver Operating Characteristic，受试者工作特征）

  上图所示记为ROC图，理想的ROC曲线是光滑的，但是基于数据画图时只能得到右边近似的结果（由于数据的有限性ROC曲线会呈现为阶梯状），当然P-R图也是近似的。

3.3.3.4 AUC

  衡量学习器好怀的直接方法也是认为包在外面的曲线代表的学习器更好（这里的外是更靠近左上角）。当出现交叉时使用曲线下方的面积（Area Under the roc Curve，AUC）来判断学习器性能的好坏，AUC大的学习器性能更好。一般来讲AUC是大于0.5的，毕竟瞎猜的准确率应该在50%，除非你的学习器正好把所有的结果都预测反了，那AUC等于0

3.3.3.5 AUC的计算方法（一）

  假定ROC曲线是由坐标为 $\{(x_1,y_1),(x_2,y_2),\cdots ,(x_N,y_N)\}$ 的点（$x_1=0,x_m=1$，$x_i,y_i$是每次根据不同阈值计算得到的真正例率和假正例率）按序连接而形成，则AUC可估算为

$$AUC=\frac{1}{2}\sum _{i=1}^{N-1}(x_{i+1}-x_i)\cdot (y_{i+1}+y_i)\text{\hspace{1em}(21)}$$

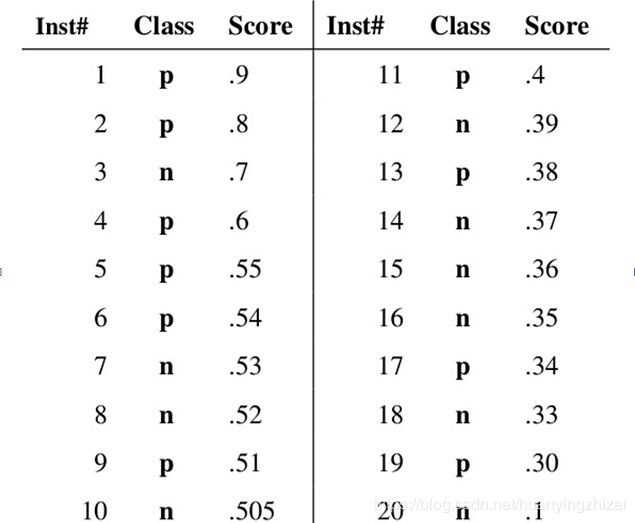
  比如下面这个例子。假设已经得出一系列样本被划分为正类的概率，然后按照大小排序，下图是一个示例，图中共有20个测试样本，“Class”一栏表示每个测试样本真正的标签（p表示正样本，n表示负样本），“Score”表示每个测试样本属于正样本的概率。

  接下来，我们从高到低，依次将“Score”值作为阈值threshold，当测试样本属于正样本的概率大于或等于这个threshold时，我们认为它为正样本，否则为负样本。举例来说，对于图中的第4个样本，其“Score”值为0.6，那么样本1，2，3，4都被认为是正样本，因为它们的“Score”值都大于等于0.6，而其他样本则都认为是负样本。每次选取一个不同的threshold，我们就可以得到一组FPR和TPR，即ROC曲线上的一点。这样一来，我们一共得到了20组FPR和TPR的值，将它们画在ROC曲线的结果如下图：

  图中所有的“$\times$”点就是我们依次把Score作为阈值计算得到的 $(TPR,FPR)$ 对。按照前面的AUC计算公式我们可以得到近似的AUC值。

$$AUC=0.68$$

  我们把这个例子用Python画出来看看

import numpy as np
import pandas as pd
from sklearn import metrics

# 因为上表给出的就是已经排好顺序的样本，所以直接写出来。当然也可以直接给出未排序的样本的
Class= np.array(['p', 'p', 'n', 'p', 'p', 'p', 'n', 'n', 'p', 'n', 'p', 'n', 'p', 'n', 'n', 'n', 'p', 'n', 'p', 'n'])
Scores = np.array([0.9, 0.8, 0.7, 0.6, 0.55, 0.54, 0.53, 0.52, 0.51, 0.505, 0.4, 0.39, 0.38, 0.37, 0.36, 0.35, 0.34, 0.33, 0.3, 0.1])

fpr, tpr, thresholds = metrics.roc_curve(y_true=Class, y_score=Scores, pos_label='p', drop_intermediate=False)

roc_point = pd.DataFrame({'FPR':fpr, 'TPR':tpr, 'thresholds':thresholds})
roc_point

  上面第一行的threshold表示没有样本被预测，认为设定其值为 $\max (y\_score)+1$

print('AUC: %s'%metrics.auc(fpr, tpr))

AUC: 0.68

# 直接计算AUC，但是只能用数字标签，更大的值代表正例
Class= np.array([1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 0])
Scores = np.array([0.9, 0.8, 0.7, 0.6, 0.55, 0.54, 0.53, 0.52, 0.51, 0.505, 0.4, 0.39, 0.38, 0.37, 0.36, 0.35, 0.34, 0.33, 0.3, 0.1])

print('AUC: %s'%metrics.roc_auc_score(y_true=Class, y_score=Scores))

AUC: 0.6799999999999999

import matplotlib.pyplot as plt

fig = plt.figure(dpi=120)

plt.plot(fpr, tpr, label='ROC curve')
plt.plot([0, 1], [0, 1], linestyle='--')
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('')
plt.legend()
plt.grid()

plt.show()

3.3.3.6 AUC的计算方法（二）

  AUC还有另一种计算方式，该方法不需要计算TPR和FPR，因此也不需要提前对样本进行排序。它和Wilcoxon-Mann-Witney Test有一些联系（为什么这两个是等价的暂不清楚）。从Mann–Whitney U statistic的角度来解释，AUC表示随机挑选一对正样本和负样本，当前分类算法依据计算出的Score将正样本排在负样本前面的概率（这也是AUC的实际意义）。它反映了分类算法的排序能力。

  由于样本的有限性，我们无法得到这个概率值，但是可以近似的去估计它。最简单的方法就是用频率进行估计，即挑选出所有的正负样本对，看看有多少样本对中，正样本的Score大于负样本的Score，若成立记一个；若正样本的Score等于负样本的Score，则记0.5个。记正样本为 $x^{+}$，负样本为 $x^{-}$，设所有样本中正样本有 $N^{+}$ 个，负样本有 $N^{-}$ 个，正负样本集合为 $D^{+}$，$D^{-}$。那么正负样本对有 $N^{+}\cdot N^{-}$ 个，得到

$$AUC=\frac{1}{N^{+}\times N^{-}}\sum _{x^{+}\in D^{+}}\sum _{x^{-}\in D^{-}}\left(\mathbb{I}(Score(x^{+})>Score(x^{-})+\frac{1}{2}\mathbb{I}(Score(x^{+})=Score(x^{-}))\right)\text{\hspace{1em}(22)}$$

  前面的例子中样本太多了，正负样本对有100个，不方便讲解，我们只取6、7、8、9号四个样本来说明用这种方法如何计算AUC

Inst#	Class	Score
6	p	0.54
7	n	0.53
8	n	0.52
9	p	0.51

  我们得到正负样本对：$(6,7)$、$(6,8)$、$(9,7)$、$(9,8)$，在 $(6,7)$ 中正样本被预测为正例的概率 0.54 大于负样本被预测为正例的概率0.53，记为1，同理 $(6,8)$ 也记为1，在 $(9,7)$ 中正样本被预测为正例的概率 0.51 小于负样本被预测为正例的概率0.53，记为0，同理 $(9,8)$ 也记为0。于是这 4 个样本的AUC为：

$$AUC=\frac{1}{2\times 2}(1+1+0+0)=0.5$$

  因为每一对样本都要进行一次判断，所以用这种方法计算AUC的时间复杂度为 $O(N^2)$。有一个可以提高计算效率的方法，它的想法是先对所有的样本按照Score进行从大到小排序（Score相同的样本前后顺序无所谓），然后赋予每个样本一个Rank值，Score最大的样本Rank值为 $N$，然后依次是 $N-1,N-2,\cdots ,2,1$。对于Score值相同的样本让它们的Rank值为平均值（比如有两个样本A、B的Score值为0.7，Rank值为2、3，那么取平均值后的Rank值都为2.5）。于是给出AUC的计算公式：

$$AUC=\frac{1}{N^{+}\times N^{-}}\left(\sum _{x^{+}\in D^{+}}Rank(x^{+})-\frac{1}{2}{N}^{+}(N^{+}+1)\right)\text{\hspace{1em}(23)}$$

  其实这个公式比较容易理解，对样本进行排名后，先看第一个正样本 $x_1^{+}$，和后面的所有样本配成 $Rank(x_1^{+})-1$ 对， 其中和正样本的配对是不需要计算的，所以再减去 $N^{+}-1$（减 1 是因为自己没有和自己配对），所以该样本对于AUC的贡献是 $Rank(x_1^{+})-N^{+}$；那么第二个正样本 $x_2^{+}$，和后面的所有样本配成 $Rank(x_2^{+})-1$ 对， 其中和正样本的配对是不需要计算的，所以再减去 $N^{+}-2$（减 2 是因为自己没有和自己配对并且没有和前一个正样本配对），所以该样本对于AUC的贡献是 $Rank(x_2^{+})-(N^{+}-1)$。以此类推最后一个正样本 $x_{N^{+}}^{+}$，和后面的所有样本配成 $Rank(x_{N^{+}}^{+})-1$ 对， 其中和正样本的配对是不需要计算的，所以再减去 $0$（因为是最后一个正样本所以后面没有正样本了），所以该样本对于AUC的贡献是 $Rank(x_{N^{+}}^{+})-1$。综上

$$\begin{array}{rl}AUC& =\frac{1}{N^{+}\times N^{-}}\sum _{i=1}^{N^{+}}\left(Rank(x_i^{+})-(N^{+}-i+1)\right)\\ & =\frac{1}{N^{+}\times N^{-}}\left(\sum _{x^{+}\in D^{+}}Rank(x^{+})-\frac{1}{2}{N}^{+}(N^{+}+1)\right)\end{array}$$

  按照这个公式我们再计算一下最开始的例子的AUC值，因为已经进行了排名，所以Rank值从是20到1，则

$$AUC=\frac{1}{10\times 10}\left((20+19+17+16+15+12+10+8+4+2)-\frac{1}{2}\times 10\times (10+1)\right)=0.68$$

3.3.3.7 AUC 和&ACC

  在论文a Better Measure than Accuracy in Comparing Learning Algorithms中提到了AUC和ACC相反的一种情况，即AUC大反而ACC小。其原因是ACC是基于一个较佳的截断值判断的，比如在上面的例子中，学习器可能认为Score大于0.7的样本是正样本，那么ACC = 0.6；可能认为Score大于0.6的样本是正样本，那么ACC = 0.55；可能认为Score大于0.5的样本是正样本，那么ACC = 0.6。可以看到ACC是和我们人为选择的截断值有关的。而AUC是基于整体进行判断的，它将每一个Score作为阈值进行计算，再求一个整体。所以AUC是一个更加稳定的准则。论文给出的建议是选择AUC更大的模型进行后续的分析。

  从公式的角度我们也可以解释这一现象。

  另外论文还提到AUC更适合评价偏态分布的模型（正负样本比例不平衡）

3.3.3.8 ROC Vs PR（AUC Vs AUCPR）

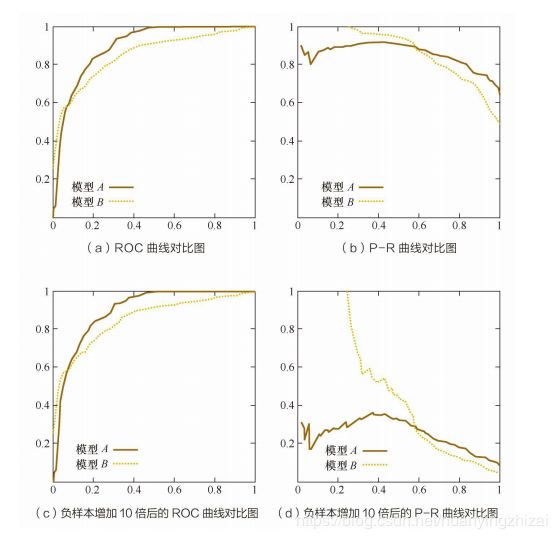
  从图(a)和图©可以看出，负样本增加10倍后，ROC曲线变化不大。分析一下为什么变化不大，其Y轴是TPR，x轴是FPR，当固定一个threshold来计算TPR和FPR的时候，虽然负样本增加了10倍，也就是FPR的分母虽然变大了，但是正常概率来讲，这个时候超过threshold的负样本量也会随之增加，也就是分子也会随之增加，所以总体FPR变化不大；而TPR是不变的。从这个角度来看的话正负样本稍微不均衡的话，对KS影响也不大（后面会讲到KS），因为KS=max(TPR-FPR)。这个前提是正负样本的量都比较大的情况下，因为只有样本量比较大的情况下，根据大数定律，计算出来的频率才非常接近于真实的概率值，有资料显示正负样本都超过6000的量，计算的频率就比较接近概率。所以在样本量都不是很大的情况下，如果样本还极端不均衡的话，就会有一些影响。由此可见，ROC曲线能够尽量降低不同测试集带来的干扰，更加客观地衡量模型本身的性能。

  从图(b)和图(d)可以看出，负样本增加10倍后，PR曲线变化比较大。也分析一下为什们变化大，其Y轴是precision，x轴是recall，当负样本增加10倍后，在racall不变的情况下，必然召回了更多的负样本（TP不变，FP变大，即precision的分母变大），所以精确度会大幅下降，图(b)和图(d)示也非常明显的反映了这一状况，所以PR曲线变化很大，也就是说PR曲线对正负样本分布比较敏感。

  如何选择呢？

•   在很多实际问题中，正负样本数量往往很不均衡。比如，计算广告领域经常涉及转化率模型，正样本的数量往往是负样本数量的1/1000，甚至1/10000。若选择不同的测试集，P-R曲线的变化就会非常大，而ROC曲线则能够更加稳定地反映模型本身的好坏。所以，ROC曲线的适用场景更多，被广泛用于排序、推荐、广告等领域。

•   但需要注意的是，选择P-R曲线还是ROC曲线是因实际问题而异的，如果研究者希望更多地看到模型在特定数据集上的表现，P-R曲线则能够更直观地反映其性能。

•   PR曲线比ROC曲线更加关注正样本，而ROC则兼顾了两者。

•   AUC越大，反映出正样本的预测结果更加靠前（分类准确度更高），推荐的样本更能符合用户的喜好

•   当正负样本比例失调时，比如正样本1个，负样本100个，则ROC曲线变化不大，此时用PR曲线更加能反映出分类器性能的好坏。这个时候指的是两个分类器，因为只有一个正样本，所以在画auc的时候变化可能不太大；但是在画PR曲线的时候，因为要召回这一个正样本，看哪个分类器同时召回了更少的负样本，差的分类器就会召回更多的负样本，这样precision必然大幅下降，这样分类器性能对比就出来了。

3.3.3.9 AUC的优势

  AUC对样本类别是否均匀并不敏感，也就是说面对不同的测试集AUC能够能加稳定地反映模型本身的好坏，这也是不均衡样本通常选择AUC作为评价准则的原因。

3.3.4 K-S曲线 与 最佳阈值的选取

  KS曲线（Kolmogorov-Smirnov，洛伦兹曲线）的数据来源和本质和ROC曲线是一致的，只是ROC曲线是把假正例率和真正例率当作横纵轴，而K-S曲线是把真正例率和假正例率都当作是纵轴，横轴则由样本的百分比来充当。KS指标用于模型风险区分能力进行评估，指标衡量的是好坏样本累计分布之间的差值。好坏样本累计差异越大，KS指标越大，那么模型的风险区分能力越强（区分正负样本能力越强）。当任务更关注正负样本的区分度时，KS指标优于AUC。另外我们也可以根据KS曲线选择用来判定正负样本的最佳阈值，即KS指标对应的阈值。

  K-S曲线的作图步骤是：

  (1) 根据分类模型返回的预测为正样本的概率（Score）对样本进行排序；

  (2) 选定一组阈值，可以是把 0-1 之间 N 等分（N 一般取 10），以等分点为阈值；

  (3) 对每个阈值计算TPR和FPR并进行描点作图（这里要注意横轴并不是阈值，而是样本的百分比，比如我们要把数据10等分，那么应该分别拿10%对应的样本的Score作为阈值。拿前面的例子举例，比如0%对应没有样本，这时TPR、FPR都是0，0%是横坐标，两个0是纵坐标；10%对应前两个样本，选择第二个样本的Score作为阈值计算此时的TPR、FPR，这时10%是横坐标，计算得出的TPR、FPR是纵坐标），就可以得到两条KS曲线。

  KS值就是两条曲线垂直间距最大的间距的绝对值。表示了模型将正负样本区分开的能力，值越大，模型预测的越准。KS值小于0.2认为模型没有区分能力

  继续使用前面的例子用Python画出KS曲线（选择样本的Score作为阈值）

print('KS: %0.2f'%max(tpr - fpr))

KS: 0.40

def plot_ks(tpr, fpr, thresholds, n=10):
    '''
    画KS曲线函数
    Param：
        tpr：metrics.roc_curve(drop_intermediate=False)返回的tpr结果
        fpr: metrics.roc_curve(drop_intermediate=False)返回的fpr结果
        thresholds：metrics.roc_curve(drop_intermediate=False)返回的thresholds结果
        n：横坐标，即样本划分百分比
    Return：
        ks_value: KS指标
    '''
    size = tpr.shape[0] - 1
    percent_coordinate = np.linspace(0, 1, n+1)    # 横坐标（样本百分比）
    index = np.array(percent_coordinate*size, dtype = np.int)
    tpr_coordinate = tpr[index]
    fpr_coordinate = fpr[index]
    ks = tpr_coordinate - fpr_coordinate
    
    ks_value = max(ks)
    ks_index = np.where(ks==ks_value)[0][0]
    
    plt.figure(dpi=120)
    plt.plot(percent_coordinate, tpr_coordinate, label='TPR')
    plt.plot(percent_coordinate, fpr_coordinate, label='FPR')
    plt.plot(percent_coordinate, ks, label='KS')
    for i in index:
        if i==ks_index:
            plt.plot([percent_coordinate[i], percent_coordinate[i]], [fpr_coordinate[i], tpr_coordinate[i]], color='red', linestyle='--')
        else:
            plt.plot([percent_coordinate[i], percent_coordinate[i]], [fpr_coordinate[i], tpr_coordinate[i]], color='grey', linestyle='--')
    plt.text(percent_coordinate[ks_index]-0.3, tpr_coordinate[ks_index]+0.05, 
            'KS= %0.2f at Percentage=%0.2f'%(ks_value, percent_coordinate[ks_index]))
    plt.legend()
    plt.ylabel('TPR/FPR')
    plt.xlabel('')
    plt.grid()
    plt.show()
    
    
    return ks_value

plot_ks(tpr, fpr, thresholds, n=20)

  KS曲线多用于信贷场景下，将Score高于（包括等于）阈值的用户视为“bad”，小于阈值的用户视为“good”，此时KS值表示能将“bad”和“good”用户最佳区分的阈值

def PlotKS(preds, labels, n, asc):
    # preds is score: asc=1
    # preds is prob: asc=0

    pred = preds  # 预测值
    bad = labels  # 取1为bad, 0为good
    ksds = pd.DataFrame({'bad': bad, 'pred': pred})
    ksds['good'] = 1 - ksds.bad

    if asc == 1:
        ksds1 = ksds.sort_values(by=['pred', 'bad'], ascending=[True, True])
    elif asc == 0:
        ksds1 = ksds.sort_values(by=['pred', 'bad'], ascending=[False, True])
    ksds1.index = range(len(ksds1.pred))
    ksds1['cumsum_good1'] = 1.0*ksds1.good.cumsum()/sum(ksds1.good)
    ksds1['cumsum_bad1'] = 1.0*ksds1.bad.cumsum()/sum(ksds1.bad)

    if asc == 1:
        ksds2 = ksds.sort_values(by=['pred', 'bad'], ascending=[True, False])
    elif asc == 0:
        ksds2 = ksds.sort_values(by=['pred', 'bad'], ascending=[False, False])
    ksds2.index = range(len(ksds2.pred))
    ksds2['cumsum_good2'] = 1.0*ksds2.good.cumsum()/sum(ksds2.good)
    ksds2['cumsum_bad2'] = 1.0*ksds2.bad.cumsum()/sum(ksds2.bad)

    # ksds1 ksds2 -> average
    ksds = ksds1[['cumsum_good1', 'cumsum_bad1']].copy()
    ksds['cumsum_good2'] = ksds2['cumsum_good2']
    ksds['cumsum_bad2'] = ksds2['cumsum_bad2']
    ksds['cumsum_good'] = (ksds['cumsum_good1'] + ksds['cumsum_good2'])/2
    ksds['cumsum_bad'] = (ksds['cumsum_bad1'] + ksds['cumsum_bad2'])/2

    # ks
    ksds['ks'] = ksds['cumsum_bad'] - ksds['cumsum_good']
    ksds['tile0'] = range(1, len(ksds.ks) + 1)
    ksds['tile'] = 1.0*ksds['tile0']/len(ksds['tile0'])

    qe = list(np.arange(0, 1, 1.0/n))
    qe.append(1)
    qe = qe[1:]

    ks_index = pd.Series(ksds.index)
    ks_index = ks_index.quantile(q = qe)
    ks_index = np.ceil(ks_index).astype(int)
    ks_index = list(ks_index)

    ksds = ksds.loc[ks_index]
    ksds = ksds[['tile', 'cumsum_good', 'cumsum_bad', 'ks']]
    ksds0 = np.array([[0, 0, 0, 0]])
    ksds = np.concatenate([ksds0, ksds], axis=0)
    ksds = pd.DataFrame(ksds, columns=['tile', 'cumsum_good', 'cumsum_bad', 'ks'])

    ks_value = ksds.ks.max()
    ks_pop = ksds.tile[ksds.ks.idxmax()]
    #print ('ks_value is ' + str(np.round(ks_value, 4)) + ' at pop = ' + str(np.round(ks_pop, 4)))

    # chart
    plt.figure(dpi=120)
    plt.plot(ksds.tile, ksds.cumsum_good, label='cum_good',
                         color='blue', linestyle='-', linewidth=2)

    plt.plot(ksds.tile, ksds.cumsum_bad, label='cum_bad',
                        color='red', linestyle='-', linewidth=2)

    plt.plot(ksds.tile, ksds.ks, label='ks',
                   color='green', linestyle='-', linewidth=2)

    plt.axvline(ks_pop, color='gray', linestyle='--')
    plt.axhline(ks_value, color='green', linestyle='--')
    plt.axhline(ksds.loc[ksds.ks.idxmax(), 'cumsum_good'], color='blue', linestyle='--')
    plt.axhline(ksds.loc[ksds.ks.idxmax(),'cumsum_bad'], color='red', linestyle='--')
    plt.legend()
    plt.title('KS=%s ' %np.round(ks_value, 4) +  
                'at Pop=%s' %np.round(ks_pop, 4), fontsize=15)

    return ksds

  模型评价准则还有很多，不过有的只应用于特殊场景，比如Gini、Left、Gain、PSI等，有的并不常用，比如NDCG、MAP等。这里不再介绍

4 参考文献

•   《机器学习》周志华

•   评价线性模型，R平方是个好裁判吗？ | 协和八

•   衡量线性回归法的指标：MSE, RMSE和MAE

•   回归问题的性能度量标准
  

•   为什么有些 Kaggle competition 用 Root Mean Squared Logarithmic Error (RMSLE) 评估算法？

•   多元线性回归建模如何确定选择哪些解释变量？

•   sklearn.metrics.log_loss

•   Terminology and derivations from a confusion matrix

•   Precision and recall

•   AUC计算方法总结

•   a Better Measure than Accuracy in Comparing Learning Algorithms

•   Evaluation measures (information retrieval)

•   P-R曲线及与ROC曲线区别

•   深入理解KS

•   Python绘制KS曲线