感知机(Perceptron)
基础不牢,地动山摇。
感知机(Perceptron),也叫感知器,它是二分类的线性模型,在模式识别算法的历史上占有重要的地位。感知机的输入为样本的特征向量,输出为样本的类别,取![]() 和
和![]() 二值。具体方法为:给样本的每一维特征引入一个相乘的权重来表达每个特征的重要程度,然后对乘积求和后加上偏置项。将结果送入符号函数,利用符号函数的二值特性将样本划分为两类。所以,训练感知机的目标可以概括为:寻找合适的权值和偏置,使得符号函数能够将样本尽量准确地分成两类。
二值。具体方法为:给样本的每一维特征引入一个相乘的权重来表达每个特征的重要程度,然后对乘积求和后加上偏置项。将结果送入符号函数,利用符号函数的二值特性将样本划分为两类。所以,训练感知机的目标可以概括为:寻找合适的权值和偏置,使得符号函数能够将样本尽量准确地分成两类。
1. 感知机模型
假设现在有![]() 个训练样本,每个样本都有
个训练样本,每个样本都有![]() 个属性(即
个属性(即![]() 维特征)和一个类别标签,那么样本的特征空间可以表示为:
维特征)和一个类别标签,那么样本的特征空间可以表示为:
样本的类别标签向量可以表示为:![]() ,由于感知机解决的是二分类问题,所以,
,由于感知机解决的是二分类问题,所以,![]() 。
。
让我们以样本的特征空间为输入空间,以样本的类别标签向量为输出空间,定义如下函数:
![]()
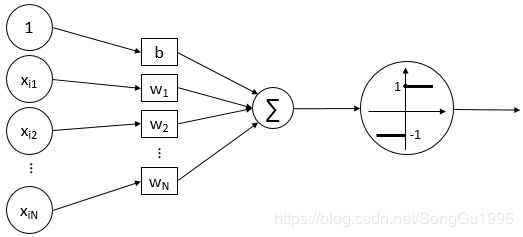
这个函数就被称为感知机模型,下图展示的是它的图形化理解。其中,![]() 和
和![]() 是感知机模型的参数,
是感知机模型的参数,![]() 是权值向量,
是权值向量,![]() 是偏置项,
是偏置项,![]() 是符号函数,符号函数的图像在下图的大圆圈中,它是感知机模型的激活函数。
是符号函数,符号函数的图像在下图的大圆圈中,它是感知机模型的激活函数。
由于使用符号函数作为激活函数,所以我们可以认为分类阈值是![]() ,即:
,即:![]() 是一个分界。我们的目标是:寻找合适的
是一个分界。我们的目标是:寻找合适的![]() 和
和![]() ,尽量使得所有
,尽量使得所有![]() 的样本
的样本![]() ,都有
,都有![]() ;所有
;所有![]() 的样本
的样本![]() ,都有
,都有![]() 。而
。而![]() 对应着特征空间中的一个超平面,其中
对应着特征空间中的一个超平面,其中![]() 是超平面的法向量,
是超平面的法向量,![]() 是超平面的截距。由此,我们可以总结出感知机模型的几何意义:在特征空间中寻找一个分离超平面,这个超平面将特征空间划分成两个部分,并且
是超平面的截距。由此,我们可以总结出感知机模型的几何意义:在特征空间中寻找一个分离超平面,这个超平面将特征空间划分成两个部分,并且![]() 类和
类和![]() 类样本点尽量位于超平面的两侧。如果想要
类样本点尽量位于超平面的两侧。如果想要![]() 类和
类和![]() 类样本严格位于超平面两侧,特征空间需要满足线性可分。
类样本严格位于超平面两侧,特征空间需要满足线性可分。
2. 感知机训练算法
经过上一节的学习,我们知道了感知机模型的目标是:求得一个能将![]() 类样本点和
类样本点和![]() 类样本点尽可能分开的超平面,即寻找合适的参数
类样本点尽可能分开的超平面,即寻找合适的参数![]() 和
和![]() 。我们采用的学习策略是:定义关于
。我们采用的学习策略是:定义关于![]() 和
和![]() 的损失函数,最小化这个损失函数。感知机模型采用的损失函数是错误分类点到超平面的总距离。首先我们来了解一下特征空间中任一样本点
的损失函数,最小化这个损失函数。感知机模型采用的损失函数是错误分类点到超平面的总距离。首先我们来了解一下特征空间中任一样本点![]() 到超平面
到超平面![]() 的距离公式(其中,
的距离公式(其中,![]() 代表
代表![]() 的L2范数):
的L2范数):
对于任一被错误分类的样本点![]() 来说,当真实标签
来说,当真实标签![]() 时,
时,![]() 反而小于
反而小于![]() ;当真实标签
;当真实标签![]() 时,
时,![]() 反而大于
反而大于![]() 。所以,对任一被错误分类的样本点
。所以,对任一被错误分类的样本点![]() ,都有
,都有![]() 成立。因此,误分类样本点
成立。因此,误分类样本点![]() 到超平面
到超平面![]() 的距离为:
的距离为:
假设被当前超平面错误分类的样本点集合为![]() ,那么所有错误分类点到当前超平面的总距离为:
,那么所有错误分类点到当前超平面的总距离为:
显然,损失函数![]() 是非负的,如果没有错误分类的样本点,损失函数的值就是
是非负的,如果没有错误分类的样本点,损失函数的值就是![]() 。而且,错误分类点越少,错误分类点离超平面越近,损失函数的值就越小。因此,我们只要找到令损失函数取最小值时对应的参数
。而且,错误分类点越少,错误分类点离超平面越近,损失函数的值就越小。因此,我们只要找到令损失函数取最小值时对应的参数![]() 和
和![]() ,就可以得到想要的感知机模型。在最小化损失函数时,我们用梯度下降法更新参数,我们并不是一次使
,就可以得到想要的感知机模型。在最小化损失函数时,我们用梯度下降法更新参数,我们并不是一次使![]() 中所有误分类样本点的梯度都下降,而是一次随机选取一个误分类点使其梯度下降。假设
中所有误分类样本点的梯度都下降,而是一次随机选取一个误分类点使其梯度下降。假设![]() 是随机选取的一个误分类点,则按照下式对
是随机选取的一个误分类点,则按照下式对![]() 和
和![]() 进行更新(其中
进行更新(其中![]() 是学习率):
是学习率):
![]()
![]()
下面给出训练感知机模型的步骤:
输入:特征空间![]()
类别标签![]()
学习率![]()
① 选取初始参数![]() 和
和![]() ,一般都取为
,一般都取为![]()
② 从训练集随机选取数据![]()
③ 如果![]() ,即选取的数据是误分类点,则更新参数,并记录此时的损失函数值
,即选取的数据是误分类点,则更新参数,并记录此时的损失函数值
④ 重复②③,将训练集中所有样本点都遍历一遍
⑤ 重复②③④,直至损失函数值为![]() (即没有错误分类点)或迭代次数达到设定值
(即没有错误分类点)或迭代次数达到设定值
输出:损失函数值最小时对应的![]() 和
和![]() ,感知机模型为
,感知机模型为![]()
需要注意的是,若样本的特征空间是线性可分的,那么感知机可以训练至没有误分类点,即损失函数值为![]() ,若样本特征空间不是线性可分的,那么损失函数无法训练至
,若样本特征空间不是线性可分的,那么损失函数无法训练至![]() ,只能选取损失函数最小时对应的参数,并且此时肯定会存在误分类点,但是没办法,谁让它线性不可分呢。另外,感知机训练算法采用不同的初始参数或者按不同的样本顺序遍历训练集,最终得到的解可以不同。
,只能选取损失函数最小时对应的参数,并且此时肯定会存在误分类点,但是没办法,谁让它线性不可分呢。另外,感知机训练算法采用不同的初始参数或者按不同的样本顺序遍历训练集,最终得到的解可以不同。
3. 实例
假设我们有三个训练样本,每个样本只有两维特征。在三个样本中,正样本有两个,分别为:![]() ,
,![]() ,负样本有一个,为:
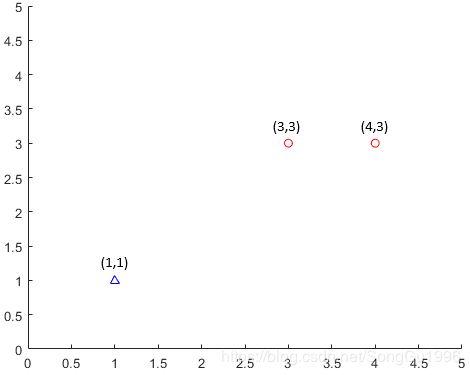
,负样本有一个,为:![]() ,题目要求是,求出能将正负样本分开的感知机模型。由于特征空间是二维的,所以我们可以很容易地将三个样本点在坐标系中表示出来(如下图所示)。很明显,这三个样本是线性可分的,即我们可以将感知机的损失函数训练至
,题目要求是,求出能将正负样本分开的感知机模型。由于特征空间是二维的,所以我们可以很容易地将三个样本点在坐标系中表示出来(如下图所示)。很明显,这三个样本是线性可分的,即我们可以将感知机的损失函数训练至![]() 。
。
对这个例子构建感知机模型:![]()
① 取初始参数值![]() ,
,![]()
![]() ,设置学习率
,设置学习率![]()
② 选取![]() ,它是正样本,
,它是正样本,![]() ,所以这是错误分类点,利用第二节中的式子更新参数
,所以这是错误分类点,利用第二节中的式子更新参数![]() ,
,![]() ,更新参数后的损失函数值为:7
,更新参数后的损失函数值为:7
③ 选取![]() ,它是正样本,
,它是正样本,![]() ,这是正确分类点;
,这是正确分类点;
④ 选取![]() ,它是负样本,
,它是负样本,![]() ,所以这是错误分类点,利用第二节中的式子更新参数
,所以这是错误分类点,利用第二节中的式子更新参数![]() ,
,![]() ,更新参数后的损失函数值为:4
,更新参数后的损失函数值为:4
⑤ 选取![]() ,它是正样本,
,它是正样本,![]() ,这是正确分类点;
,这是正确分类点;
⑥ 选取![]() ,它是正样本,
,它是正样本,![]() ,这是正确分类点;
,这是正确分类点;
⑦ 选取![]() ,它是负样本,
,它是负样本,![]() ,所以这是错误分类点,利用第二节中的式子更新参数
,所以这是错误分类点,利用第二节中的式子更新参数![]() ,
,![]() ,更新参数后的损失函数值为:1
,更新参数后的损失函数值为:1
⑧ 选取![]() ,它是正样本,
,它是正样本,![]() ,所以这是正确分类点;
,所以这是正确分类点;
⑨ 选取![]() ,它是正样本,
,它是正样本,![]() ,所以这是正确分类点;
,所以这是正确分类点;
⑩ 选取![]() ,它是负样本,
,它是负样本,![]() ,所以这是错误分类点,利用第二节中的式子更新参数
,所以这是错误分类点,利用第二节中的式子更新参数![]() ,
,![]() ,更新参数后的损失函数值为:4
,更新参数后的损失函数值为:4
⑪ 选取![]() ,它是正样本,
,它是正样本,![]() ,所以这是错误分类点,利用第二节中的式子更新参数
,所以这是错误分类点,利用第二节中的式子更新参数![]() ,
,![]() ,更新参数后的损失函数值为:4
,更新参数后的损失函数值为:4
⑫ 选取![]() ,它是正样本,
,它是正样本,![]() ,所以这是正确分类点;
,所以这是正确分类点;
⑬ 选取![]() ,它是负样本,
,它是负样本,![]() ,所以这是错误分类点,利用第二节中的式子更新参数
,所以这是错误分类点,利用第二节中的式子更新参数![]() ,
,![]() ,更新参数后的损失函数值为:2
,更新参数后的损失函数值为:2
⑭ 选取![]() ,它是正样本,
,它是正样本,![]() ,所以这是正确分类点;
,所以这是正确分类点;
⑮ 选取![]() ,它是正样本,
,它是正样本,![]() ,所以这是正确分类点;
,所以这是正确分类点;
⑯ 选取![]() ,它是负样本,
,它是负样本,![]() ,所以这是错误分类点,利用第二节中的式子更新参数
,所以这是错误分类点,利用第二节中的式子更新参数![]() ,
,![]() ,更新参数后的损失函数值为:0
,更新参数后的损失函数值为:0
经过这么多步骤以后,损失函数已经为![]() ,符合停止条件,不需要继续迭代,最终得到的感知机模型为:
,符合停止条件,不需要继续迭代,最终得到的感知机模型为:
![]()
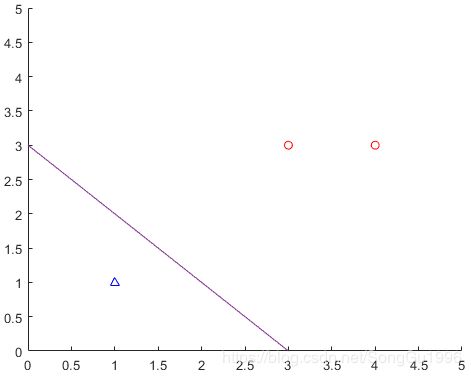
与参数对应的分割超平面(在本例中为二维空间下的一条直线)如下图所示:
参考:
https://blog.csdn.net/ouyangfushu/article/details/85289070
https://www.cnblogs.com/huangyc/p/9706575.html
《深度学习 一起玩转TensorLayer》董豪 等编著
《统计学习方法》李航 著