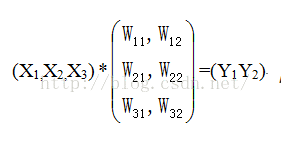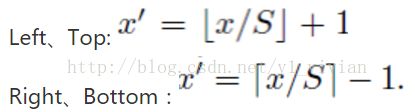SPP-Net论文详解

SPP-Net是出自2015年发表在IEEE上的论文-《Spatial Pyramid Pooling in Deep ConvolutionalNetworks for Visual Recognition》。

在此之前，所有的神经网络都是需要输入固定尺寸的图片，比如224*224（ImageNet）、32*32(LenNet)、96*96等。这样对于我们希望检测各种大小的图片的时候，需要经过crop，或者warp等一系列操作，这都在一定程度上导致图片信息的丢失和变形，限制了识别精确度。而且，从生理学角度出发，人眼看到一个图片时，大脑会首先认为这是一个整体，而不会进行crop和warp，所以更有可能的是，我们的大脑通过搜集一些浅层的信息，在更深层才识别出这些任意形状的目标。

为什么要固定输入图片的大小？

       卷积层的参数和输入大小无关，它仅仅是一个卷积核在图像上滑动，不管输入图像多大都没关系，只是对不同大小的图片卷积出不同大小的特征图，但是全连接层的参数就和输入图像大小有关，因为它要把输入的所有像素点连接起来,需要指定输入层神经元个数和输出层神经元个数，所以需要规定输入的feature的大小。
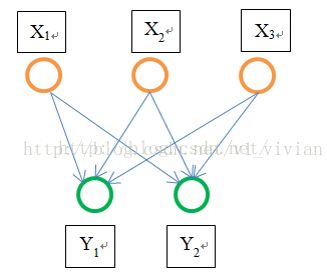
       因此，固定长度的约束仅限于全连接层。以下图为例说明：

                             

            作为全连接层，如果输入的x维数不等，那么参数w肯定也会不同，因此，全连接层是必须确定输入，输出个数的。

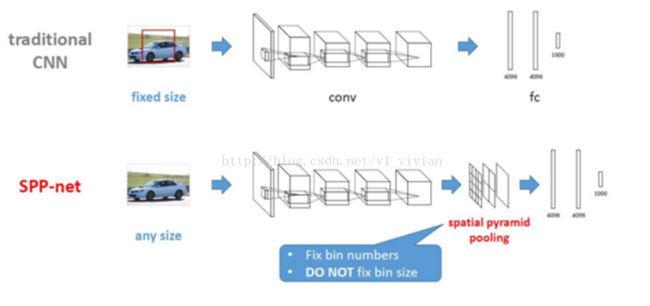
SPP-Net是如何调整网络结构的？

        SPP-Net在最后一个卷积层后，接入了金字塔池化层，使用这种方式，可以让网络输入任意的图片，而且还会生成固定大小的输出。

什么是金字塔池化？

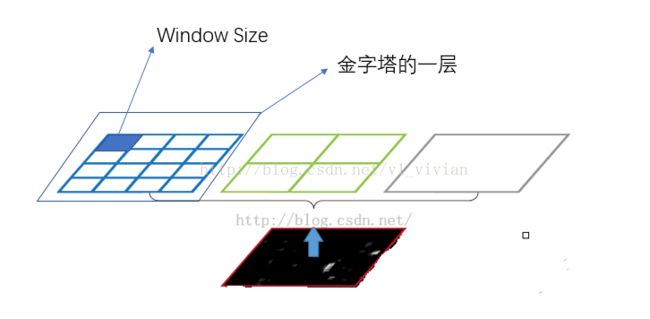
以下图为例进行解释说明：

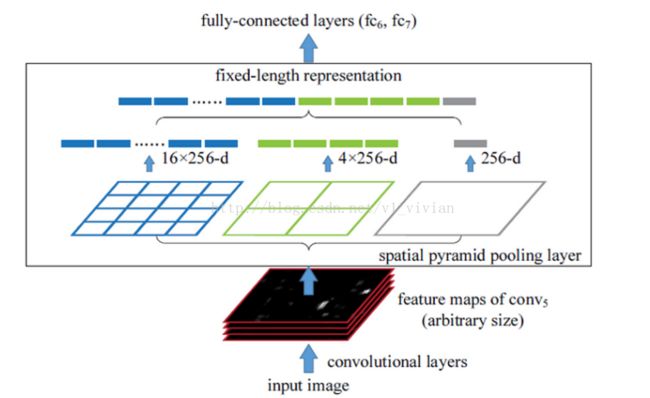
       黑色图片代表卷积之后的特征图，接着我们以不同大小的块来提取特征，分别是4*4，2*2，1*1，将这三张网格放到下面这张特征图上，就可以得到16+4+1=21种不同的块(Spatial bins)，我们从这21个块中，每个块提取出一个特征，这样刚好就是我们要提取的21维特征向量。这种以不同的大小格子的组合方式来池化的过程就是空间金字塔池化（SPP）。比如，要进行空间金字塔最大池化，其实就是从这21个图片块中，分别计算每个块的最大值，从而得到一个输出单元，最终得到一个21维特征的输出。

从整体过程来看，就是如下图所示：

         输出向量大小为Mk，M=#bins， k=#filters，作为全连接层的输入。

         例如上图，所以Conv5计算出的feature map也是任意大小的，现在经过SPP之后，就可以变成固定大小的输出了，以上图为例，一共可以输出（16+4+1）*256的特征。

金字塔池化的意义是什么？

      总结而言，当网络输入的是一张任意大小的图片，这个时候我们可以一直进行卷积、池化，直到网络的倒数几层的时候，也就是我们即将与全连接层连接的时候，就要使用金字塔池化，使得任意大小的特征图都能够转换成固定大小的特征向量，这就是空间金字塔池化的意义（多尺度特征提取出固定大小的特征向量）。

网络训练阶段：

       论文中将网络的训练分为两种：一种是single-size,一种是Multi-size。

先讲解single-size的训练过程：

理论上说，SPP-net支持直接以多尺度的原始图片作为输入后直接BP即可。实际上，caffe等实现中，为了计算的方便，GPU,CUDA等比较适合固定尺寸的输入，所以训练的时候输入是固定了尺度了的。以224*224的输入为例：

在conv5之后的特征图为：13x13（a*a）
金字塔层bins:   n*n
将pooling层作为sliding window pooling。
windows_size=[a/n] 向上取整 ， stride_size=[a/n]向下取整。

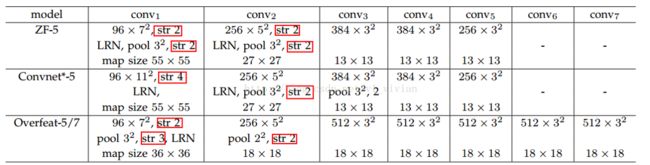
例如论文中给出的参数如下：

对于pool 3*3:      sizeX=5 的计算公式是：[13/3]向上取整=5 ，stride = 4的计算公式是：[13/3]向下取整。

如果输入改成180x180，这时候conv5出来的reponse map为10x10，类似的方法，能够得到新的pooling参数。

        

       对于Multi-size training即就是：使用两个尺度进行训练：224*224 和180*180

       训练的时候，224x224的图片通过crop得到，180x180的图片通过缩放224x224的图片得到。之后，迭代训练，即用224的图片训练一个epoch，之后180的图片训练一个epoch，交替地进行。

        两种尺度下，在SSP后，输出的特征维度都是(9+4+1)x256，参数是共享的，之后接全连接层即可。

        论文中说，这样训练的好处是可以更快的收敛。

网络测试阶段

 输入为任意大小的图片

SPP-Net与R-CNN的对比

对于R-CNN，整个过程是：

1. 首先通过选择性搜索，对待检测的图片进行搜索出~2000个候选窗口。 
2. 把这2k个候选窗口的图片都缩放到227*227，然后分别输入CNN中，每个proposal提取出一个特征向量，也就是说利用CNN对每个proposal进行提取特征向量。 
3. 把上面每个候选窗口的对应特征向量，利用SVM算法进行分类识别。 

可以看出R-CNN的计算量是非常大的，因为2k个候选窗口都要输入到CNN中，分别进行特征提取。

而对于SPP-Net，整个过程是：

1. 首先通过选择性搜索，对待检测的图片进行搜索出2000个候选窗口。这一步和R-CNN一样。
2.  特征提取阶段。这一步就是和R-CNN最大的区别了，这一步骤的具体操作如下：把整张待检测的图片，输入CNN中，进行一次性特征提取，得到feature maps，然后在feature maps中找到各个候选框的区域，再对各个候选框采用金字塔空间池化，提取出固定长度的特征向量。而R-CNN输入的是每个候选框，然后在进入CNN，因为SPP-Net只需要一次对整张图片进行特征提取，速度会大大提升。
3. 最后一步也是和R-CNN一样，采用SVM算法进行特征向量分类识别。

Mapping a Window to Feature Maps

我们知道，在原图中的proposal,经过多层卷积之后，位置还是相对于原图不变的（如下图所示），那现在需要解决的问题就是，如何能够将原图上的proposal,映射到卷积之后得到的特征图上，因为在此之后我们要对proposal进行金字塔池化。

 对于映射关系，论文中给出了一个公式：

假设(x’,y’)表示特征图上的坐标点，坐标点(x,y)表示原输入图片上的点，那么它们之间有如下转换关系，这种映射关心与网络结构有关： (x,y)=(S*x’,S*y’)

反过来，我们希望通过(x,y)坐标求解(x’,y’)，那么计算公式如下：

其中S就是CNN中所有的strides的乘积，包含了池化、卷积的stride。

比如，对于下图的集中网络结构，S的计算如下：

 论文中使用的是 ZF-5：             S=2*2*2*2=16
              Overfeat-5/7 :               S =2*3*2 =12

检测算法

对于检测算法，论文中是这样做到：使用ss生成~2k个候选框，缩放图像min(w,h)=s之后提取特征，每个候选框使用一个4层的空间金字塔池化特征，网络使用的是ZF-5的SPPNet形式。之后将12800d的特征输入全连接层，SVM的输入为全连接层的输出。

这个算法可以应用到多尺度的特征提取：先将图片resize到五个尺度：480，576，688，864，1200，加自己6个。然后在map window to feature map一步中，选择ROI框尺度在｛6个尺度｝中大小最接近224x224的那个尺度下的feature maps中提取对应的roi feature。这样做可以提高系统的准确率。

对于SPP-Net和其他网络的对比效果这里就不在做过多解释。

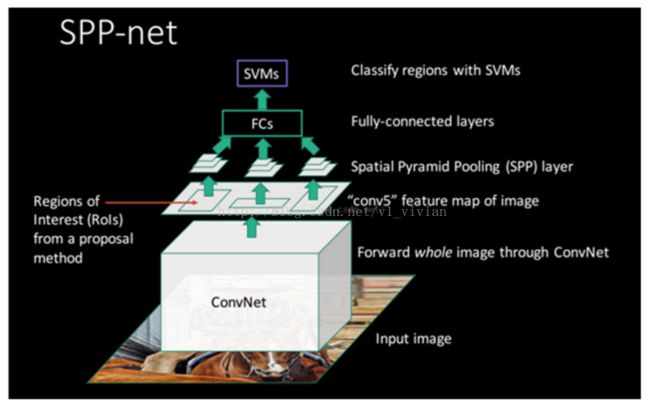
完整的SPP-Net

最后，用一张图来完整的描述SPP-Net。