《机器学习西瓜书》学习笔记——第三章_线性模型:线性回归
1. 线性模型_基本形式
1.1 定义
回归分析(regression analysis)是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。
回归分析按照涉及的变量的多少,分为一元回归和多元回归分析;按照因变量的多少,可分为简单回归分析和多重回归分析;按照自变量和因变量之间的关系类型,可分为线性回归分析和非线性回归分析。如果在回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。如果回归分析中包括两个或两个以上的自变量,且自变量之间存在线性相关,则称为多重线性回归分析。
线性分类器
给定一些数据点,它们分别属于两个不同的类,现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点,用y表示类别(y可以取1或者0,分别代表两个不同的类),一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper plane),这个超平面的方程可以表示为( w T w^T wT中的T代表转置):
ω T \omega^T ωT x x x + b = 0 b=0 b=0
所以,线性模型向量形式为:
y ^ = ω T \hat{y} = \omega^T y^=ωT x x x + b b b
ω \omega ω, b b b为需要学习的参数
ω \omega ω直观表达了各属性在预测中的重要性,因此线性模型有很好的解释性。
2. 经典的线性模型介绍
线性回归(linear regression) & 对数几率回归(logistic regression)
- 二者虽然都叫回归,实质不同。简单说回归问题和分类问题区别如下:
回归问题:连续输出,如预测房价
分类问题:离散输出,如二分类问题输出0或1
本文重点介绍线性回归,对数几率回归在下文中介绍
2.1 线性回归简介(linear regression)
假设一个样本我们用 x x x来表示,数据集中第k个样本则为 x k x_k xk。一个样本中存在d个特征值,用一个列向量来表示一个样本 x k = ( x k 1 ; x k 2 ; x k 3 ; . . . ; x k d ) x_k = (x_k^1;x_k^2;x_k^3;...;x_k^d) xk=(xk1;xk2;xk3;...;xkd)具有 d d d个特征。 w w w是待学习的权重,因为每个样本中有 d d d个特征,因此 w w w是一个 d d d维的列向量,记为 w = ( w 1 ; w 2 ; w 3 , . . . , w d ) w=(w_1;w_2;w_3,...,w_d) w=(w1;w2;w3,...,wd)。在 w w w和 b b b确定的的情况下,模型就能确定为 y ^ = w T x + b \hat{y} = w^Tx + b y^=wTx+b。
- 数据输入: 给定数据集 D = ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) D={(x_1,y_1),(x_2,y_2),…,(x_m,y_m)} D=(x1,y1),(x2,y2),…,(xm,ym), y i yi yi∈R
- 参数权重: w = ( w 1 ; w 2 ; w 3 , . . . , w d ) w=(w_1;w_2;w_3,...,w_d) w=(w1;w2;w3,...,wd)
2.2 最小二乘法(几何意义求解)
确定 w w w和 b b b的方式在于衡量 y ^ \hat{y} y^和 y y y之间的差别。
线性模型用一个直线(平面)拟合数据点,找出一个最好的直线(平面)即要求每个真实点距离平面的距离最近。
一种方法是使得残差平方和(Residual Sum of Squares, RSS)最小:
R S S ( y , y ^ ) RSS(y,\hat{y}) RSS(y,y^)= ∑ i = 1 m ( y i − y ^ i ) 2 \sum_{i=1}^m(y_i - \hat{y}_i)^2 ∑i=1m(yi−y^i)2
另一种情况下,为消除样本量的差异,也会用最小化均方误差(MSE)拟合:
M S E ( y , y ^ ) MSE(y,\hat{y}) MSE(y,y^)= 1 m 1\over m m1 ∑ i = 1 m ( y i − y ^ i ) 2 \sum_{i=1}^m(y_i - \hat{y}_i)^2 ∑i=1m(yi−y^i)2
我们用均方误差来衡量模型的性能(西瓜书P54省略1/m),试图让误差最小化,此时的 w w w和 b b b即为所需。则:
( w ∗ w^* w∗, b ∗ b^* b∗)= a r g m i n argmin argmin ∑ i = 1 m ( y i − y ^ i ) 2 = \sum_{i=1}^m(y_i - \hat{y}_i)^2 = ∑i=1m(yi−y^i)2=arg m i n min min ∑ i = 1 m ( y i − w T x i − b ) 2 \sum_{i=1}^m(y_i - w^Tx_i - b)^2 ∑i=1m(yi−wTxi−b)2
基于均方误差最小化来进行模型求解的方法称为“最小二乘法”。
线性回归中就是试图找到一条直线,使所有样本到直线上的欧式距离之和最小。(西瓜书P54,均方误差对应于欧氏距离)
求解 w w w和 b b b使均方误差最小的过程,称为线性回归模型的最小二乘“参数估计”。
2.3 最大似然估计(概率意义求解)
参考此处
2.4 一元线性回归(最小二乘法适用于一元线性回归)
设 d d d=1,则对损失函数L分别对w和b求偏导得:
∂ L ( w , b ) ∂ w = − 2 ∑ i = 1 m ( x i y i − w x i 2 − b x i ) \frac{\partial L(w,b)}{\partial w} = -2 \sum_{i=1}^m(x_iy_i - wx_i^2 - bx_i) ∂w∂L(w,b)=−2∑i=1m(xiyi−wxi2−bxi)
∂ L ( w , b ) ∂ b = − 2 ∑ i = 1 m ( y i − w x i − b ) \frac{\partial L(w,b)}{\partial b} = -2 \sum_{i=1}^m(y_i - wx_i - b) ∂b∂L(w,b)=−2∑i=1m(yi−wxi−b)
令 ∂ L ( w , b ) ∂ b = 0 \frac{\partial L(w,b)}{\partial b} = 0 ∂b∂L(w,b)=0得 b ∗ = 1 m ∑ i = 1 m ( y i − w x i ) b^* = {1\over m}\sum_{i=1}^m(y_i - wx_i) b∗=m1∑i=1m(yi−wxi)
令 ∂ L ( w , b ) ∂ w = 0 \frac{\partial L(w,b)}{\partial w} = 0 ∂w∂L(w,b)=0得 w ∗ = ∑ i = 1 m y i ( x i − x ‾ ) ∑ i = 1 m x i 2 − 1 m ( ∑ i = 1 m x i ) 2 w^*={\sum_{i=1}^my_i(x_i-\overline x) \over \sum_{i=1}^mx_i^2 - {1\over m}( \sum_{i=1}^mx_i)^2} w∗=∑i=1mxi2−m1(∑i=1mxi)2∑i=1myi(xi−x)
其中 x ‾ \overline x x= 1 m ∑ i = 1 m x i {1\over m}\sum_{i=1}^mx_i m1∑i=1mxi为 x x x的均值。
- 模型输出: f ( x i ) = w ∗ x i + b ∗ f(x_i)=w^*x_i+b^* f(xi)=w∗xi+b∗
2.5 多元线性回归
上面的公式推导是基于 x x x的维度d=1的情况,在更一般的情况下d并不等于1,也就是我们一开始讨论的 y = w T x + b y^=w^Tx+b y=wTx+b,此时线性模型叫做多元线性回归。
为了方便讨论,记 w ^ = ( w ; b ) , X = ( x 1 T , 1 ; x 2 T , 1 ; . . . ; x m T , 1 ) \hat{w} = (w;b), X=(x_1^T,1; x_2^T, 1; ...; x_m^T, 1) w^=(w;b),X=(x1T,1;x2T,1;...;xmT,1),
那么 y ^ = X w ^ \hat{y} = X\hat{w} y^=Xw^,
损失函数为 L ( w , b ) = L ( w ^ ) = ( y − X w ^ ) T ( y − X w ^ ) L(w,b)=L(\hat{w})=(y-X\hat{w})^T(y-X\hat{w}) L(w,b)=L(w^)=(y−Xw^)T(y−Xw^)
L ( w ^ ) L(\hat{w}) L(w^)对 w ^ \hat{w} w^求偏导: ∂ L ( w ^ ) w ^ = 2 X T ( X w ^ − y ) \frac{\partial L(\hat{w})}{\hat{w}} = 2X^T(X\hat{w} - y) w^∂L(w^)=2XT(Xw^−y)
令偏导等于0,得 w ^ ∗ = ( X T X ) − 1 X T y \hat{w}^* = (X^TX)^{-1}X^Ty w^∗=(XTX)−1XTy由此确定模型。
在现实任务中,大量变量时,可求解出多个 w ^ \hat{w} w^都能使均方误差最小化,选择哪一个解作为输出可由学习算法的归纳偏好决定,可引入正则化项。
- 模型输出: f ( x i ) = w ^ ∗ T X f(x_i)=\hat{w}^{*T}X f(xi)=w^∗TX
PS:对数线性回归
即让模型预测值逼近 y y y的衍生物
l n y lny lny= w T x + b w^Tx+b wTx+b, 让 e w T x + b e^{w^Tx+b} ewTx+b逼近 y y y,
该式仍为线性回归,但已求输入空间到输出空间的非线性函数映射
一般的,单调可微g( .),
y = g − 1 ( w T x + b ) y=g^{-1}(w^Tx+b) y=g−1(wTx+b)
称为“广义线性模型”,g(.)为联系函数。对数线性回归是其一种特例。
----------9/5 23:48 敲公式敲到脑壳疼^^
2.6 多元线性回归梯度下降求解
梯度下降参考此处
最小二乘法和梯度下降关系
2.7 评估方法
R 2 = 1 − R S S T S S R^2=1-{RSS\over TSS} R2=1−TSSRSS
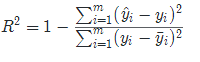
2.8 算法实践
线性回归算法代码应用
2.9 具体应用场景举例
- 身高和体重的关系
- 房屋面积和房价的关系
- …
2.10 总结
- 优点: 实现简单,计算简单,应用简便
- 缺点: 非线性数据拟合效果不理想,现实生活中数据的特征和目标之间并不是简单的线性组合,所以并不能很好的解决具体问题。
- 通过实际值和预测值的误差计算损失函数,最小化损失函数对应的参数构成线性回归的模型,利用该模型去预测别的数据。
- 线性回归常用于数据特征稀疏,并且数据过大的问题中,可以通过线性回归进行特征筛选。在比赛中也可以用线性回归做一个Baseline。
参考:https://blog.csdn.net/Datawhale/article/details/82931967
2.11 补充问题解答
- 线性回归可解释性较好,是否可用于特征的选择参考?
- 原因:LinearRegression训练后,使用 model.coef_得到模型的参数,参数越大表示权重越大
- 线性回归,Ridge回归(L2范式),Lasso回归(L1范式)的区别
- 监督学习的过程可以概括为:最小化误差的同时规则化参数。最小化误差是为了让模型拟合训练数据,规则化参数是为了防止过拟合。参数过多会导致模型复杂度上升,产生过拟合,即训练误差很小,但测试误差很大,这和监督学习的目标是相违背的。所以需要采取措施,保证模型尽量简单的基础上,最小化训练误差,使模型具有更好的泛化能力(即测试误差也很小)。
所以,在基本的最小化误差的公司上加上规则化参数的过程,构成Ridge回归和Lasso回归,具体讲解见链接:L1,L2详解
