周志华《机器学习》(西瓜书) ——相关数学知识整理:拉格朗日乘子法与KKT条件
文章目录
- 0 简介
- 1 无约束条件
- 2 等式约束条件
- 3 不等式约束条件
0 简介
在求解最优化问题中,拉格朗日乘子法(Lagrange Multiplier)是一种比较最常用的方法。当求解带不等式约束的最优化问题时,通常会将原问题转化为对偶问题进行求解,这时往往会要求函数满足 KKT 条件。
这里提到的最优化问题通常是指凸优化问题,即对某一给定的凸函数,求其在指定作用域上的全局最小值(求最大值问题很容易转化成求最小值问题,然后按求最小值问题进行求解)。
求最优化问题一般会碰到以下三种情况:
- 无约束条件
- 等式约束条件
- 不等式约束条件
1 无约束条件
首先考虑不带任何约束的优化问题:
min x ∈ R n f ( x ) \min _{\boldsymbol{x}\in \mathbb{R}^{n}}f(\boldsymbol{x}) x∈Rnminf(x)
这是最简单的情况,直接令梯度为零 ∇ x f ( x ) = 0 \nabla_{\boldsymbol{x}} f(\boldsymbol{x})=0 ∇xf(x)=0 即可,若没有解析解,可用梯度下降法或者牛顿法进行迭代求解。
2 等式约束条件
当目标函数加上等式约束条件之后,问题变成如下形式:
min x f ( x ) s.t. h i ( x ) = 0 , i = 1 , 2 , … , m \begin{array}{ll}&{\min _{\boldsymbol{x}}}{f(\boldsymbol{x})} \\\\ &{\text {s.t.}} \ \ {h_{i}(\boldsymbol{x})=0,i=1,2, \ldots, m}\end{array} minxf(x)s.t. hi(x)=0,i=1,2,…,m
约束条件将解的范围限定在一个可行域内,此时不一定能找到使 ∇ x f ( x ) = 0 \nabla_{\boldsymbol{x}} f(\boldsymbol{x})=0 ∇xf(x)=0 的点,这时需要在可行域内找到使 f ( x ) f(\boldsymbol{x}) f(x) 取最小值的点,这时常用拉格朗日乘子法,引入拉格朗日乘子 α ∈ R m \boldsymbol{\alpha} \in \mathbb{R}^{m} α∈Rm ,构造拉格朗日函数如下:
L ( x , α ) = f ( x ) + ∑ i = 1 m α i h i ( x ) L(\boldsymbol{x}, \boldsymbol{\alpha})=f(\boldsymbol{x})+\sum_{i=1}^{m} \alpha_{i} h_{i}(\boldsymbol{x}) L(x,α)=f(x)+i=1∑mαihi(x)
分别令 L ( x , α ) L(\boldsymbol{x}, \boldsymbol{\alpha}) L(x,α) 对 x \boldsymbol{x} x 和 α \boldsymbol{\alpha} α 的梯度为 0 0 0
{ ∇ x L ( x , α ) = 0 ∇ α L ( x , α ) = 0 \left\{\begin{array}{l}{\nabla_{\boldsymbol{x}} L(\boldsymbol{x}, \boldsymbol{\alpha})=0} \\\\ {\nabla_{\boldsymbol{\alpha}} L(\boldsymbol{x}, \boldsymbol{\alpha})=0}\end{array}\right. ⎩⎨⎧∇xL(x,α)=0∇αL(x,α)=0
将求得 x \boldsymbol{x} x 、 α \boldsymbol{\alpha} α 后将 x \boldsymbol{x} x 带回,即得到 f ( x ) f(\boldsymbol{x}) f(x) 在 h i ( x ) = 0 h_{i}(\boldsymbol{x})=0 hi(x)=0 约束下的最小值。
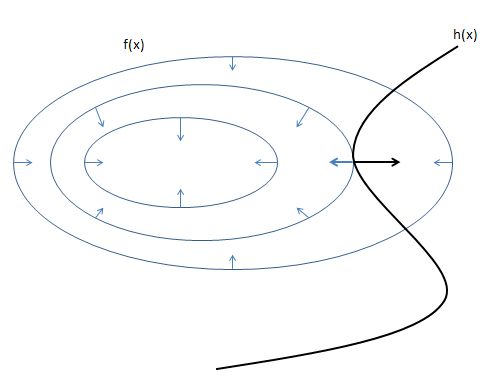
下图是带一个等式约束条件的优化问题的示例。
L ( x , α ) = f ( x ) + α h ( x ) L(\boldsymbol{x}, \alpha)=f(\boldsymbol{x})+\alpha h(\boldsymbol{x}) L(x,α)=f(x)+αh(x)
从图中我们可以看出,只有在 f ( x ) f(\boldsymbol{x}) f(x) 和 h ( x ) h(\boldsymbol{x}) h(x) 相切的点,才有可能得到满足约束的 f ( x ) f(\boldsymbol{x}) f(x) 的极小值,此时 f ( x ) f(\boldsymbol{x}) f(x) 和 h ( x ) h(\boldsymbol{x}) h(x) 的梯度必定是平行的,即
∇ x f ( x ) = λ ∇ x h ( x ) \nabla_{\boldsymbol{x}} f(\boldsymbol{x}) = \lambda \nabla_{\boldsymbol{x}}h(\boldsymbol{x}) ∇xf(x)=λ∇xh(x)
当我们利用拉格朗日乘子法求
∇ x L ( x , α ) = ∇ x f ( x ) + α ∇ x h ( x ) = 0 \nabla_{\boldsymbol{x}}L(\boldsymbol{x}, \alpha)=\nabla_{\boldsymbol{x}} f(\boldsymbol{x}) + \alpha\nabla_{\boldsymbol{x}}h(\boldsymbol{x})=0 ∇xL(x,α)=∇xf(x)+α∇xh(x)=0
时,很容易得到
∇ x f ( x ) = − α ∇ x h ( x ) \nabla_{\boldsymbol{x}} f(\boldsymbol{x}) = -\alpha \nabla_{\boldsymbol{x}}h(\boldsymbol{x}) ∇xf(x)=−α∇xh(x)
这也印证了梯度平行的情况。
另外,
∇ α L ( x , α ) = 0 \nabla_{\boldsymbol{\alpha}} L(\boldsymbol{x}, \boldsymbol{\alpha})=0 ∇αL(x,α)=0
就是
h ( x ) = 0 h(\boldsymbol{x})=0 h(x)=0
综上,我们就能理解带等式约束的拉格朗日乘子法的算法意义了。
我们看一个例子:
min x , y ( x 2 + y 2 ) s.t. x + y = 1 \begin{array}{ll}&{\min _{x,y}}{(x^2+y^2)} \\\\ &{\text {s.t.}} \ \ {x+y=1}\end{array} minx,y(x2+y2)s.t. x+y=1
解:
构造拉格朗日函数:
L ( x , y , α ) = ( x 2 + y 2 ) + α ( x + y − 1 ) \begin{array}{ll}&{L(x,y,\alpha)=(x^2+y^2)+\alpha(x+y-1)}\end{array} L(x,y,α)=(x2+y2)+α(x+y−1)
令偏导为 0 0 0
{ ∇ x L ( x , y , α ) = 0 ∇ y L ( x , y , α ) = 0 ∇ α L ( x , y , α ) = 0 \left\{\begin{array}{l}{\nabla_{x} L(x,y,\alpha)=0} \\\\ {\nabla_{y} L(x,y,\alpha)=0} \\\\ {\nabla_{\alpha} L(x,y,\alpha)=0}\end{array}\right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧∇xL(x,y,α)=0∇yL(x,y,α)=0∇αL(x,y,α)=0
得
{ 2 x + α = 0 2 y + α = 0 x + y − 1 = 0 \left\{\begin{array}{l}{2x+\alpha=0} \\\\ {2y+\alpha=0} \\\\ {x+y-1=0}\end{array}\right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧2x+α=02y+α=0x+y−1=0
解得
{ x = 1 2 y = 1 2 α = − 1 \left\{\begin{array}{l}{x=\frac{1}{2}} \\\\ {y=\frac{1}{2}} \\\\ {\alpha=-1}\end{array}\right. ⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧x=21y=21α=−1
原问题的最优值是
( 1 2 ) 2 + ( 1 2 ) 2 = ( 1 2 ) (\frac{1}{2})^2+(\frac{1}{2})^2=(\frac{1}{2}) (21)2+(21)2=(21)
当然,我们可以用代入法通过配方直接得到结论
y = 1 − x , 代 入 , 有 x 2 + ( 1 − x ) 2 = x 2 + x 2 − 2 x + 1 = 2 ( x − 1 2 ) 2 + 1 2 y=1-x,代入,有 \\ {x}^{2}+(1-x)^{2}=x^2+x^2-2x+1=2(x-\frac{1}{2})^{2}+\frac{1}{2} y=1−x,代入,有x2+(1−x)2=x2+x2−2x+1=2(x−21)2+21
这和用拉格朗日乘子法得到的结论是一致的。
3 不等式约束条件
当目标函数再加上不等式约束条件之后,问题变成如下形式:
min x f ( x ) s.t. h i ( x ) = 0 , i = 1 , 2 , … , m g i ( x ) ⩽ 0 , i = 1 , 2 , … , n \begin{array}{c}{\min_\boldsymbol{x} f(\boldsymbol{x})} \\\\ {\text {s.t.} \ \ {h_{i}(\boldsymbol{x})=0,i=1,2, \ldots, m}} \\\\ {g_{i}(\boldsymbol{x}) \leqslant 0,i=1,2, \ldots, n}\end{array} minxf(x)s.t. hi(x)=0,i=1,2,…,mgi(x)⩽0,i=1,2,…,n
引入拉格朗日乘子 α ∈ R m , β ∈ R n \boldsymbol{\alpha} \in \mathbb{R}^{m},\boldsymbol{\beta} \in \mathbb{R}^{n} α∈Rm,β∈Rn ,得
L ( x , α , β ) = f ( x ) + ∑ i = 1 m α i h i ( x ) + ∑ i = 1 n β i g i ( x ) L(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta})=f(\boldsymbol{x})+\sum_{i=1}^{m} \alpha_{i} h_{i}(\boldsymbol{x})+\sum_{i=1}^{n} \beta_{i} g_{i}(\boldsymbol{x}) L(x,α,β)=f(x)+i=1∑mαihi(x)+i=1∑nβigi(x)
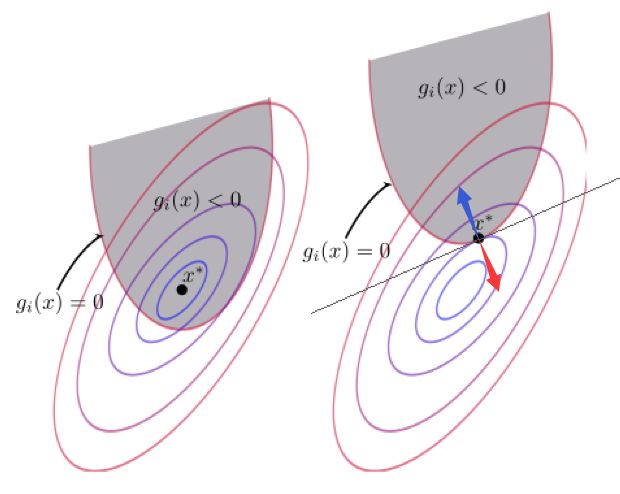
等式约束条件前面分析过了,这里我们只关注不等式约束条件,以下图中的 g i ( x ) g_i(\boldsymbol{x}) gi(x) 为例。
图中的椭圆圈为函数 f ( x ) f({\boldsymbol{x}}) f(x) 的等值线,红色抛物线是 g i ( x ) g_i(\boldsymbol{x}) gi(x) 的边界。易知,最优点要么出现在 g i ( x ) < 0 g_i(\boldsymbol{x})<0 gi(x)<0 的区域内,要么在边界 g i ( x ) = 0 g_i(\boldsymbol{x})=0 gi(x)=0 上。
当最优点要出现在 g i ( x ) < 0 g_i(\boldsymbol{x})<0 gi(x)<0 的区域内时,实际上 g i ( x ) < 0 g_i(\boldsymbol{x})<0 gi(x)<0 的约束是不起作用的,我们可以直接把它忽略掉,即令它的系数 β i = 0 \beta_i=0 βi=0。
当最优点要出现在边界 g i ( x ) = 0 g_i(\boldsymbol{x})=0 gi(x)=0 上时,和前面的等式约束是类似的,最优点也是在 f ( x ) f(\boldsymbol{x}) f(x) 和 g i ( x ) g_i(\boldsymbol{x}) gi(x) 的切点上,并且两函数在该点的梯度平行。不过这里还有一个更严格的要求,就是在此时 g i ( x ) g_i(\boldsymbol{x}) gi(x) 与 f ( x ) f(\boldsymbol{x}) f(x) 的梯度必须是反向的。在最优点 g i ( x ) g_i(\boldsymbol{x}) gi(x) 的梯度方向指向灰色区域的外部,如红色箭头所示,而 f ( x ) f(\boldsymbol{x}) f(x) 的梯度方向则指向圈变大的方向,如蓝色箭头所示,所以这里的 β i > 0 \beta_i>0 βi>0。
综上, β i ⩾ 0 \beta_i\geqslant0 βi⩾0 ,再加上已知条件 h i ( x ) = 0 h_i(\boldsymbol{x})=0 hi(x)=0 , g i ( x ) ⩽ 0 g_i(\boldsymbol{x})\leqslant0 gi(x)⩽0 ,可知
L ( x , α , β ) = f ( x ) + ∑ i = 1 m α i h i ( x ) + ∑ i = 1 n β i g i ( x ) ⩽ f ( x ) L(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta})=f(\boldsymbol{x})+\sum_{i=1}^{m} \alpha_{i} h_{i}(\boldsymbol{x})+\sum_{i=1}^{n} \beta_{i} g_{i}(\boldsymbol{x})\leqslant f(\boldsymbol{x}) L(x,α,β)=f(x)+i=1∑mαihi(x)+i=1∑nβigi(x)⩽f(x)
即
f ( x ) = max α , β L ( x , α , β ) f(\boldsymbol{x})=\max_{\boldsymbol{\alpha},\boldsymbol{\beta}}L(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) f(x)=α,βmaxL(x,α,β)
这样,就有
min x f ( x ) = min x max α , β L ( x , α , β ) \min_{\boldsymbol{x}}f(\boldsymbol{x})=\min_{\boldsymbol{x}}\max_{\boldsymbol{\alpha},\boldsymbol{\beta}}L(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) xminf(x)=xminα,βmaxL(x,α,β)
原问题简单说,就是求最大值的最小值,它的对偶问题,就是求最小值的最大值,即
max α , β min x L ( x , α , β ) \max_{\boldsymbol{\alpha},\boldsymbol{\beta}}\min_{\boldsymbol{x}}L(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) α,βmaxxminL(x,α,β)
显然,对偶问题的最优值,要比原问题的最优值小,即
max α , β min x L ( x , α , β ) ⩽ min x max α , β L ( x , α , β ) \max_{\boldsymbol{\alpha},\boldsymbol{\beta}}\min_{\boldsymbol{x}}L(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) \leqslant \min_{\boldsymbol{x}}\max_{\boldsymbol{\alpha},\boldsymbol{\beta}}L(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) α,βmaxxminL(x,α,β)⩽xminα,βmaxL(x,α,β)
这时的对偶问题,是弱对偶问题,满足的条件是弱对偶条件。
如果我们希望原问题和其对偶问题的最值相等,还需要怎样的约束条件呢?假设最优解为 x ∗ \boldsymbol{x}^* x∗ , α ∗ \boldsymbol{\alpha}^* α∗ , β ∗ \boldsymbol{\beta}^* β∗ ,则原问题和对偶问题的最优值都为 f ( x ∗ ) f(\boldsymbol{x}^*) f(x∗) ,故
f ( x ∗ ) = max α , β min x L ( x , α , β ) = max α , β min x ( f ( x ) + ∑ i = 1 m α i h i ( x ) + ∑ i = 1 n β i g i ( x ) ) ⩽ f ( x ∗ ) + ∑ i = 1 m α i ∗ h i ( x ∗ ) + ∑ i = 1 n β i ∗ g i ( x ∗ ) ⩽ f ( x ∗ ) \begin{aligned} f(\boldsymbol{x}^*)&=\max_{\boldsymbol{\alpha},\boldsymbol{\beta}}\min_{\boldsymbol{x}}L(\boldsymbol{x}, \boldsymbol{\alpha}, \boldsymbol{\beta}) \\\\ &=\max_{\boldsymbol{\alpha},\boldsymbol{\beta}}\min_{\boldsymbol{x}}(f(\boldsymbol{x})+\sum_{i=1}^{m} \alpha_{i} h_{i}(\boldsymbol{x})+\sum_{i=1}^{n} \beta_{i} g_{i}(\boldsymbol{x})) \\\\ & \leqslant f(\boldsymbol{\boldsymbol{x}^*})+\sum_{i=1}^{m} \alpha_{i}^* h_{i}(\boldsymbol{\boldsymbol{x}^*})+\sum_{i=1}^{n} \beta_{i}^* g_{i}(\boldsymbol{\boldsymbol{x}^*}) \\\\ & \leqslant f(\boldsymbol{\boldsymbol{x}^*}) \end{aligned} f(x∗)=α,βmaxxminL(x,α,β)=α,βmaxxmin(f(x)+i=1∑mαihi(x)+i=1∑nβigi(x))⩽f(x∗)+i=1∑mαi∗hi(x∗)+i=1∑nβi∗gi(x∗)⩽f(x∗)
要想式中的不等号成立,就要 β i g i ( x ) = 0 \beta_{i} g_{i}(\boldsymbol{x})=0 βigi(x)=0 ,和前面已有的约束合起来写,就是
{ h i ( x ) = 0 g i ( x ) ⩽ 0 β i ⩾ 0 β i g i ( x ) = 0 \left\{\begin{array}{l}{h_i(\boldsymbol{x})=0} \\\\ {g_i(\boldsymbol{x}) \leqslant 0} \\\\ {\beta_i \geqslant 0} \\\\ {\beta_ig_i(\boldsymbol{x}) = 0} \end{array}\right. ⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧hi(x)=0gi(x)⩽0βi⩾0βigi(x)=0
这就是 KKT 条件,满足 KKT 条件,原问题的最优值和对偶问题的最优值相等,这时的对偶问题就是强对偶问题,满足的条件也称为强对偶条件。
以上,就是拉格朗日乘子法和 KKT 条件的相关介绍,这些知识在机器学习的 SVM (支持向量机)算法中有很重要的应用。
参考:
- 真正理解拉格朗日乘子法和 KKT 条件
- 深入理解拉格朗日乘子法(Lagrange Multiplier) 和KKT条件
- 约束优化方法之拉格朗日乘子法与KKT条件