机器学习（二） － 一个最简单的线性分类模拟人脑神经工作

机器学习和传统算法不同的关键在于，传统算法依靠固定的算法来处理数据，因此，算法对于数据而言，逻辑是固定的。机器学习的做法是算法是框架，需要训练数据形成逻辑，再通过逻辑去识别，判定和预测新的，或者测试数据。

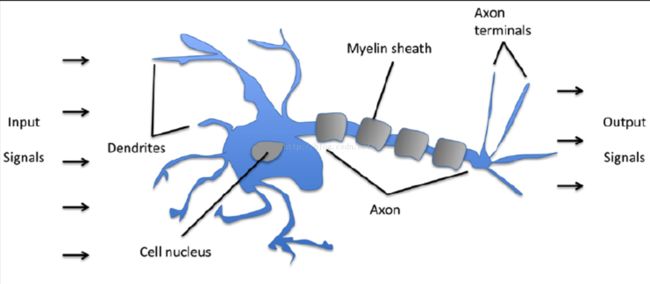
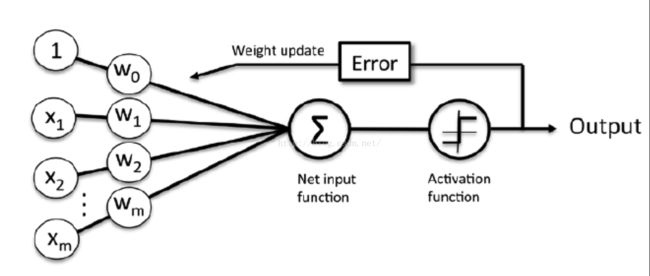
这里的框架算法构成是模拟人脑的神经系统，分成输入（树突），神经处理（神经细胞），输出（轴突终端）。很多人，包括我在内其实是抗拒数学公式的，那么在做机器学习这样不能回避公式的情况下，怎么办呢？代码来取代公式吧。我打着不发明轮子的口号，应用公式，不再推导公式。真的需要做公式推导，我也会使用代码来模拟推导过程。

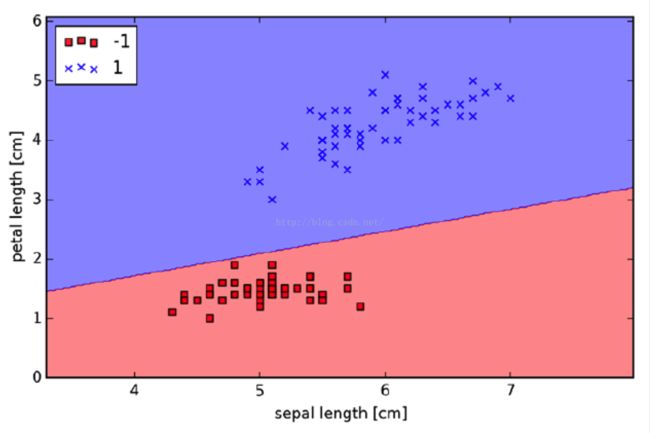
我们来看最简单的二元分类算法（该算法的具体数学实现，见我另外文章《Binary Classification 二元分类算法与Python实现及应用》）。这里假设scikit－learn，numpy和pandas这些库都已经安装和配置好了（python的机器学习工作环境安装和配置，见我另外文章《用于机器学习的Python环境搭建（Macbook Pro版）》）。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np

 
  
### - 下载原始数据
IrisDataURL = 'https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data'
df = pd.read_csv(IrisDataURL,header=None)
df.tail()
### - 选取训练子集和格式化训练数据
y = df.iloc[0:100, 4].values
y = np.where(y == 'Iris-setosa', -1, 1)
X = df.iloc[0:100, [0, 2]].values
 
  
### - 创建感知器算法器ppn，eta是学习速度，n_iter是在数据上学习多少遍
ppn = Perceptron(eta=0.1, n_iter=10) 
  
 
  
### - fit用来初始化参数矢量，记住这里矢量维度比训练集维度多一。
ppn.fit(X, y)
 
  
### - 
 
  
x1_min, x1_max = X[:, 0].min() - 1, X[:, 0].max() + 1
x2_min, x2_max = X[:, 1].min() - 1, X[:, 1].max() + 1
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, resolution),
np.arange(x2_min, x2_max, resolution))
Z = classifier.predict(np.array([xx1.ravel(), xx2.ravel()]).T)
Z = Z.reshape(xx1.shape) ＃ － 到这里分类已经完成，接下来就是分类进行可视化。
 
  
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max())
# plot class samples
for idx, cl in enumerate(np.unique(y)):
    plt.scatter(x=X[y == cl, 0], y=X[y == cl, 1],
	alpha=0.8, c=cmap(idx),
	marker=markers[idx], label=cl)
 
  
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')
plt.legend(loc='upper left')
plt.show()