Python神经网络编程学习笔记（一）

一、预测器（千米转换英里）

若简单机器接受了一个输入，并做出应有的预测，输出结果，所以我们将其称为预测器。我们根据结果与已知真实示例进行比较所得到的误差，调整内部参数，使预测更加精确。预测器的核心是有一个可调节的线性函数。

已知千米和英里之间存在线性关系：英里=千米×C，随机取C的值，目标为减少误差。

无需使用确切的方法计算出C值，采用持续细化误差的想法。我们尝试得到一个答案，并多次改进答案，这种方法也可称为迭代，意思是持续地、一点一点改进答案。

总结：

1.当我们不能精确知道一些事情如何运作时，我们可以尝试使用模型来估计其运作方式，在模型中，包括了我们可以调整的参数。如果我们不知道如何将千米转换为英里，那么我们可以使用线性函数作为模型，并使用可调节的梯度值作为参数。

2.改进这些模型的一种好方法是，基于模型和已知真实示例之间的比较，得到模型偏移的误差值，调整参数。

个人思考：预测器本身并不是为了得到精确的结果，而是通过比较，调整内部参数，从而尽可能减少输出结果的误差。所以没有必要纠结于使用公式算出精确结果。

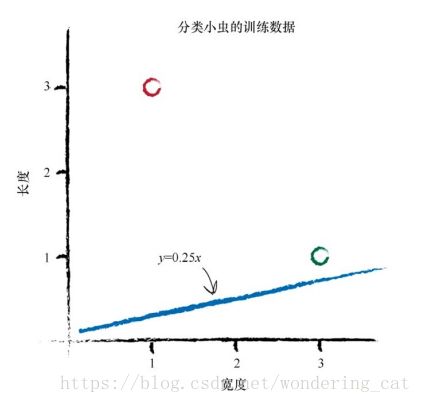
二、分类器（毛虫和瓢虫为例）

使用直线将不同性质的事物分开，即训练线性分类器，调整分界线的斜率，使其能够正确分类瓢虫或毛虫。

实例：

设置线性函数：y=Ax   y为长度，x为宽度，A为斜率参数。

不能通过观察图就画出一条合适的直线,我们希望能够找到一种可重复的方法，也就是用一系列的计算机指令来达到这个目标。计算机科学家称这一系列指令为算法

1.数字计算过程：

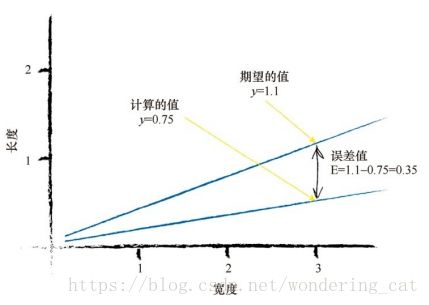
（1）随机为A取值，测试期望值与真实值。

随机取A=0.25，测试实例1，得y=0.75

设期望的目标值是1.1，误差值E为 误差值=（期望目标值-实际输出值）， E = 1.1-0.75 = 0.35

（2）寻找误差值E与A的关系

设正确的期望值为t，即目标值。

        显然得   E = t - y

                   y=Ax                       ①

                  t = (A + ΔA)x          ②      ΔA表示微小的斜率变化量

由①②可得     t -y = (A + ΔA)x - Ax    即   E=ΔAx

使用数据测试该公式的正确性：

使用（1）中的误差值E=0.35，x=3.0，A=0.25

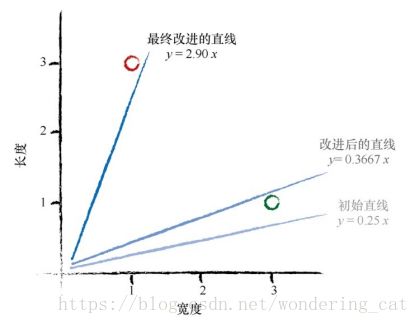
由E=ΔAx，得ΔA=0.1167，更新后的A=0.1167+0.25=0.3667

用更新后的A，得到 y=Ax=0.3667*3=1.1    

与（1）中设置的目标值相符！

（3）基于当前的误差值调整参数

使用更新后的Ａ测试实例２，x=1.0时，y=Ax=0.3667*1.0=0.3667   与y=3.0相差甚远

设置目标值为2.9，则误差值E=2.9-0.3667=2.5333    误差变得更大了！

ΔA=2.5333，A=2.5333+0.3667=2.9   

结论：我们最终改进的直线与最后一次训练样本十分匹配，但是抛弃了先前训练样本的学习结果，只对最近的一个实例进行了学习。

2.适度改进，采用学习率方法

添加一个调节系数L，ΔA= L（E / x ），调节系数通常也被称为学习率。

设置L=0.5，即只更新原更新值的一半。

（1）实例1测试

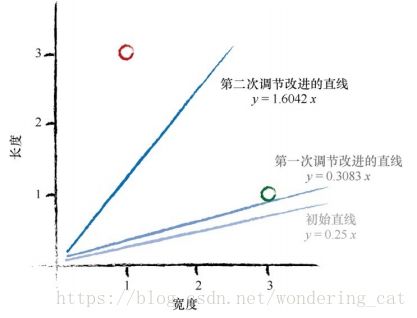
初始值A=0.25，E=0.35，x=3.0，ΔA= L（E / x ）=0.5*0.35/3.0=0.0583

A=0.0583+0.25=0.3083

y=Ax=0.3083*3.0=0.9250    与未调整前相比，向正确方向移动了。

（2）基于（1）的实例2测试

使用A=0.3083，x=1.0，y=0.3083*1.0=0.3083

所需值为2.9，误差值E=2.9-0.3083=2.5917

ΔA= L（E / x ）=0.5*2.5917/1.0=1.2958

第二个更新值A=0.3083+1.2958=1.6042

总结：

使用一般的调整方法会出现一个问题，即改进后的模型只与最后一次训练样本最匹 配，“有效地”忽略了所有以前的训练样本。解决这个问题的一种好方法是使用学习率，调节改进速率，这样单一的训练样本就不能主导整个学习过程.

个人思考：

前两次的分类器存在共同的问题：即只能对最近的一次记录进行学习，忽略了其他数据。我们采取的改进办法是增加调节系数，即利用带有学习率的改进方法。