人工智能AI:Keras PyTorch MXNet 深度学习实战(不定时更新)
norm()
1.Matlab函数中的 norm()
1.应用:norm()用于计算矩阵范数
2.格式:n = norm(A);
n = norm(A,p);
3.功能:norm函数可计算几种不同类型的矩阵范数,根据p的不同可得到不同的范数
4.如果A为矩阵
n=norm(A) 返回A的最大奇异值,即max(svd(A))
n=norm(A,p) 根据p的不同,返回不同的值
5.如果A为向量
norm(A,p) 返回向量A的p范数。即返回 sum(abs(A).^p)^(1/p),对任意 1
3.对Python的控制流求导
对如下函数进行求导:
def f(a):
b = a * 2
while b.norm().asscalar() < 1000:
b = b * 2
if b.sum().asscalar() > 0:
c = b
else:
c = 100 * b
return c
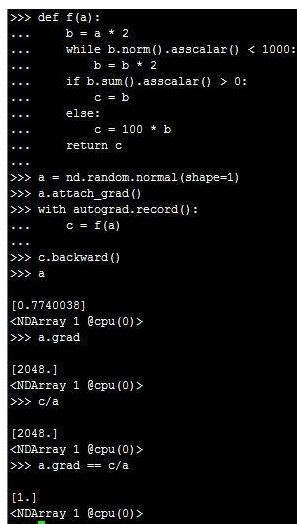
函数f(a)最后的输出值c由输入值a决定,即c=xa,导数x=c/a。
MXNet 基础入门
1.如何使用NDArray来处理数据
1.NDArray几种不同的创建方法
1.第1条:从mxnet中导入nd
2.第2条:使用arange()函数创建一个长度为12的行向量
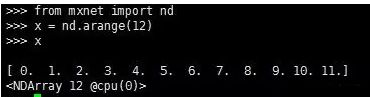
该NDArray包含12个元素(element),其值为arange(12)指定的0-11。在打印的结果中标注了属性。
其中12指的是NDArray的形状,就是向量的长度。@cpu(0)表示默认情况下NDArray被创建在CPU上。
3.第3条:使用reshape()函数修改x的形状,将x修改为一个3行4列的矩阵
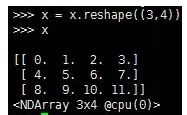
4.第4条:创建一个各元素为0,形状为(2,3,4)的张量。PS:矩阵和向量都是一种特殊的张量。
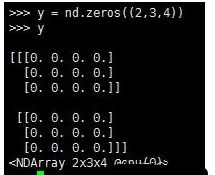
5.第5条:同理,创建一个各元素为1的张量。
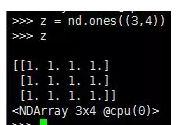
6.第6条:通过Python的列表(list)指定NDArray中每个元素的值。
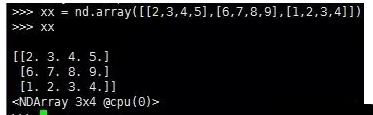
7.第7条:通过nd.random.normal()方法,随机生成NDArray每个元素的值,创建一个形状为(3,4)的NDArray。
每个元素随机采样于均值为0方差为1的正态分布。
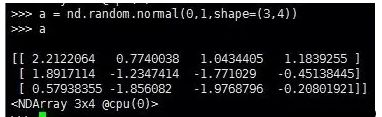
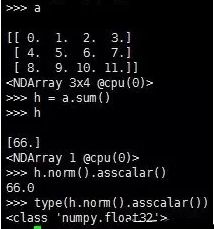
8.第8条:通过shape属性获取形状,通过size属性获取NDArray中元素的个数。
2.NDArray的运算
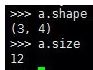
1.第1条:按元素加法
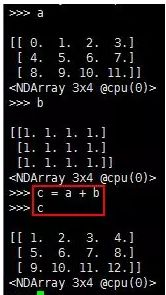
2.第2条:按元素乘法
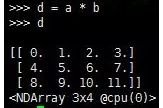
3.第3条:按元素除法
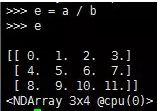
4.第4条:按元素指数运算,exp
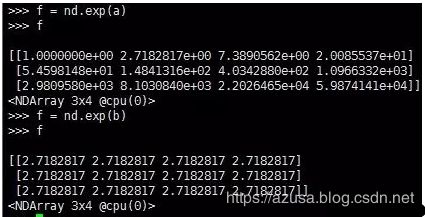
5.第5条:对矩阵b做转置,矩阵a、b做矩阵乘法操作,a为3行4列,b为4行3列,故其结果为一个3行3列的矩阵。dot
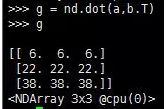
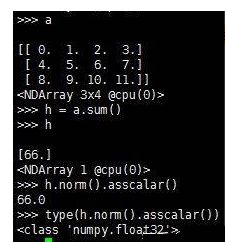
6.第6条:NDArray元素求和(结果为标量,但仍然为NDArray格式,可以通过norm().asscalar()函数转换为Python中的数),sum()
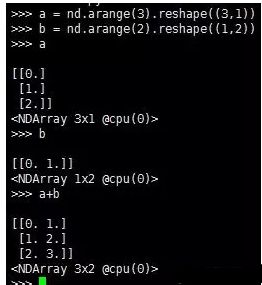
3.广播机制
上面提到的两个NDArray之间元素级的运算都是基于两个NDArray形状相同,如果两个NDArray形状不同,在运算的过程中会触发广播(broadcasting)机制,
即先把两个NDArray搞成形状相同,然后再进行运算。
广播(broadcasting)机制简单理解就是行与列间复制,达到不同NDArray之间形状相同的目的。
4.NDArray在进行运算的过程中产生的内存开销
1.第1条:每一个操作都会新开辟一块内存空间用来存储操作后的运算结果。
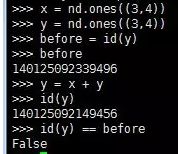
2.第2条:可以通过[:]将计算结果写入之前变量创建的内存空间中。nd.zeros_like(x)方法可以创建一个形状和x相同,但元素均为0的NDArray。
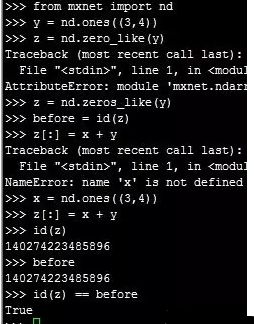
3.第3条:在第2条的运算中,虽然变量z在计算前后的内存地址相同,在本质上其运行原理仍然是先将x+y的值放到一个新开辟的内存空间中,
然后再将结果拷贝到z的内存中。
为了避免这种计算过程中的内存开销,可以使用运算符全名函数中的out参数解决该问题。

可以看到,前后的内存地址相同,这种开销也得以避免。
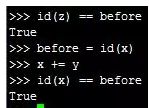
4.第4条:现有NDArray的值在之后的程序中不会复用,可以直接使用如下方法来减少内存开销。x+=y,x[:]=x+y
5.NDArray的索引
类比Python中列表(list)的索引,NDArray的索引可以理解为每一个元素的位置。索引的值从0开始逐渐递加。
举个栗子,一个3行2列的矩阵,其行索引为0,1,2,列索引为0,1。
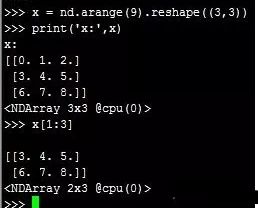
1.第1条:创建一个3行3列的矩阵x,通过x[1:3],根据Python的开闭原则,可知取的值为索引为1和2行的数据。
2.第2条:通过x[1,2]这种形式可以取出指定的元素,可以对其重新赋值。
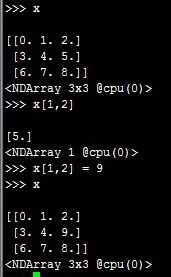
3.第3条:可以通过[1:2,1:3]这种方式取出NDArray中的多个元素,可以对这些元素进行重新赋值。
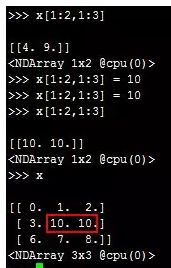
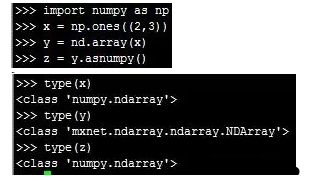
6.NDArray与NumPy格式的相互转换
可以通过array()函数将numpy转换为ndarray,通过asnumpy()函数将ndarray转化为numpy。
7.小结
NDArray是MXNet中存储和转换数据的主要工具,可以将它理解为MXNet实现的一种数据结构。
在这一节中可以了解到如何对NDArray进行创建、运算、制定索引,同时与numpy格式进行转换的方法。
2.简述MXNet提供的自动求导功能
1.很多深度学习框架需要编译计算图进行求导,而MXNet不需要,使用自带的autograd包即可实现自动求导功能。
2.下面来看两个例子。
1.第一个:对简单的数学函数进行求导
对函数y=2x^2进行求导

其中涉及的细节有一点:
1.求变量x的导数,需要先调用x.attach_grad()函数创建需要的内存空间
2.为了减少计算和内存的开销,默认情况下,MXNet不会记录用于求倒数的计算图,
我们需要需要调用autograd.record()函数来让MXNet记录有关的计算图。
3.通过y.backward()函数求倒数,其结果为x.grad
2.第二个:对Python的控制流求导
对如下函数进行求导:
def f(a):
b = a * 2
while b.norm().asscalar() < 1000:
b = b * 2
if b.sum().asscalar() > 0:
c = b
else:
c = 100 * b
return c
函数f(a)最后的输出值c由输入值a决定,即c=xa,导数x=c/a。
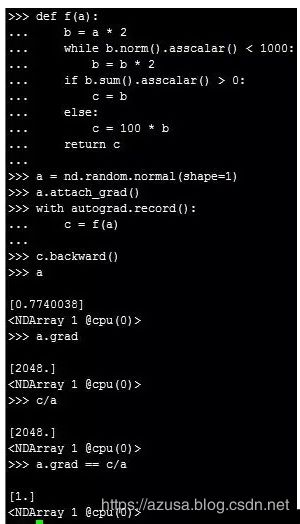
3.小结
通过MXNet自动求导总共分为3步:
1.开辟存储导数的内存空间a.attach_grad()
2.通过autograd.record()函数记录计算图,并实现相应的函数
3.调用c.backward()函数进行求导
3.如何通过ndarray和autograd实现简单的线性回归
线性回归是监督学习中的一种,是一个最简单,也是最有用的单层神经网络。
我的理解是这样的给定一些数据集X,根据训练好的模型(将数据集X带入模型中),都有一个特定的y值与其对应。训练这个模型就是我们需要做的工作。
那线性回归就是y=ax+b,我们要做的就是确定斜率a和位移b的值。
1.第1步:数据集的创建
在工业级的生产环境中,数据集往往来源于真事的业务场景(在Web日志中挖掘攻击行为呀,预测房价啊一类的),这里是演示,所以暂且使用随机生成的数据。
在第一个例子中,作者使用了一套人工生成的数据,相应的生成公式如下:y[i] = 2*X[i][0] - 3.4*X[i][1] + 4.2 + noise
noise服从均值为0方差为0.1的正态分布。
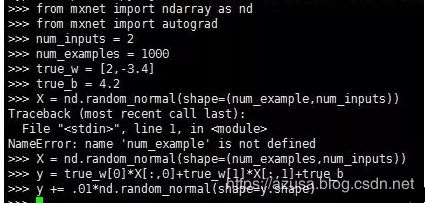
相应的代码如下:
>>> from mxnet import ndarray as nd
>>> from mxnet import autograd
>>> num_inputs = 2
>>> num_examples = 1000
>>> true_w = [2,-3.4]
>>> true_b = 4.2
>>> X = nd.random_normal(shape=(num_example,num_inputs))
Traceback (most recent call last):
File "", line 1, in
NameError: name 'num_example' is not defined
>>> X = nd.random_normal(shape=(num_examples,num_inputs))
>>> y = true_w[0]*X[:,0]+true_w[1]*X[:,1]+true_b
>>> y += .01*nd.random_normal(shape=y.shape)
2.第2步:数据读取
当我们拥有了一定的数据集之后,我们要做的就是数据的读取。不断的读取这些数据块,进行神经网络的训练。
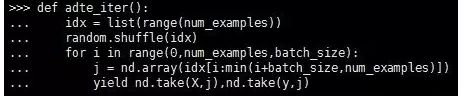
相应的函数如下:
>>> def date_iter():
... idx = list(range(num_examples))
... random.shuffle(idx)
... for i in range(0,num_examples,batch_size):
... j = nd.array(idx[i:min(i+batch_size,num_examples)])
... yield nd.take(X,j),nd.take(y,j)
通过yield关键字来构造成迭代器,依次取出不同的样本数据(10个)。
通过for loop不断的遍历将迭代器中的数据取出。
>>> for date,label in adte_iter():
... print(date,label)
... break
接下来将读取到的数据,传入我们给定的算法中进行训练。
3.第3步:定义模型
先来随机初始化模型的参数。

创建参数的梯度:

参数初始化完成后我们就可以进行模型的定义:
>>> def net(X):
... return nd.dot(X,w)+b
4.第4步:定义损失函数
通过损失函数衡量预测目标与真实目标之间的差距。
def square_loss(yhat,y):
return (yhat - y.reshape(yhat.shape))**2
5.第5步:优化
使用梯度下降进行求解。
def SGD(params,lr):
for param in params:
param[:] = param - lr * param.grad
6.第6步:训练
>>> epochs = 5
>>> learning_rate = .001
>>>
>>> for e in range(epochs):
... total_loss = 0
... for data,label in adte_iter():
... with autograd.record():
... output = net(data)
... loss = square_loss(output,label)
... loss.backward()
... SGD(params,learning_rate)
... total_loss += nd.sum(loss).asscalar()
... print("%d,loss: %f" % (e,total_loss/num_examples))
...
0,loss: 0.130911
1,loss: 0.002628
2,loss: 0.000150
3,loss: 0.000102
4,loss: 0.000101

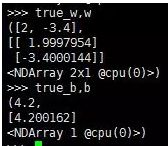
查看训练结果(和我们的预期相同)
4.使用gluon的线性回归
1.第1步:数据集的创建
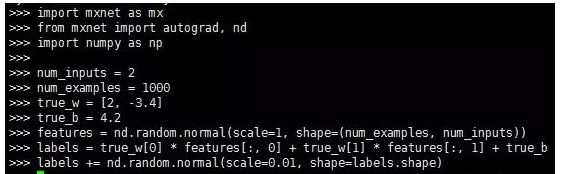
2.第2步:数据读取

3.第3步:定义模型
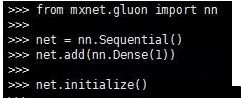
4.第4步:定义损失函数
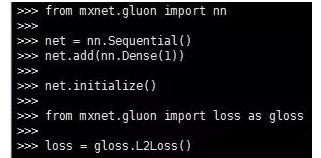
5.第5步:优化

6.第6步:训练
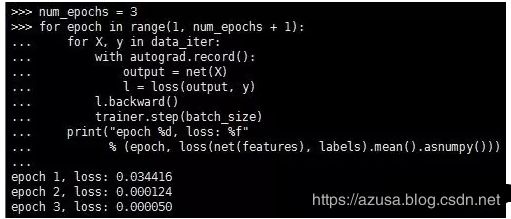
5.总结
1.确认需要训练的数据集(特征工程)
2.将特征工程后的数据读取至内存中
3.定义模型同时初始化模型参数
4.定义损失函数、优化算法
5.训练模型及验证结果





































