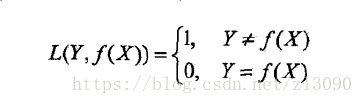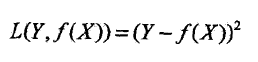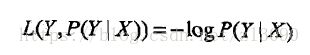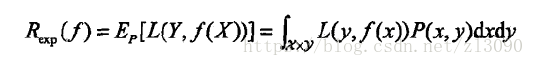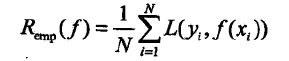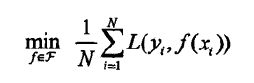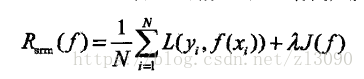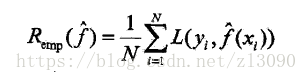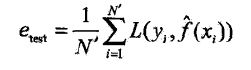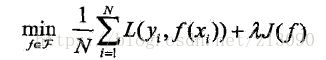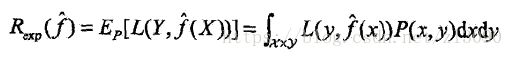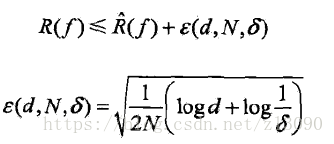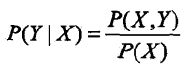【统计学习方法-李航-笔记总结】一、统计学习方法概述

看李航老师的书有感，做做笔记以便后续查阅，也方便同道中的大佬们参考~

本部分包括:

1. 统计学习概述

2.  统计学习三要素

3.  模型的评估与选择

4.  分类问题、标注问题与回归问题

 

1. 统计学习概述

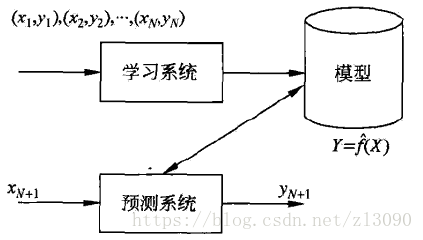
（1）概念：统计学习是关于计算机基于数据构建概率统计模型并运用模型对数据进行预测分析的学科。

（2）特点：

        a. 建立在计算机与网络上的；

        b. 以数据为研究对象；

        c. 目的是对数据进行预测与分析；

        d. 以方法为中心，构建模型；

        e. 涉及概率论、统计学、计算机等的交叉学科

（3）方法：监督学习、非监督学习、半监督学习和强化学习等

（4）步骤：

         a. 得到一个有限的训练数据集合；

         b. 确定包含所有可能的模型的假设空间，即学习模型的集合；

         c. 确定模型选则的准则，即策略；

         d. 实现求解最优模型的算法，即算法；

         e. 选择最优的算法；

         f. 利用最优模型对新数据进行预测或分析。

2. 统计学习三要素：

    统计学习方法 = 模型 + 策略 + 算法

（1）模型：要学习的条件概率分布或决策函数

（2）策略：选择最优模型的准则

         a.  损失函数：预测错误程度的度量，损失函数值越小，模型越好

               0-1损失函数：

        

               平方损失函数：

               

               绝对损失函数：

            

               对数损失函数：

            

     损失函数细节参见博客：https://blog.csdn.net/heyongluoyao8/article/details/52462400

      b.  风险函数（期望损失）：即损失函数的期望

      

            这是模型f(X）关于联合分布P(X,Y)的平均意义下的损失，称为风险函数或损失函数。

            学习的目标就是选择期望风险最小的模型，但由于联合分布P(X,Y)未知，R不能直接计算。

       c. 经验风险（经验损失函数）：模型关于训练集（训练样本）的平均损失

                      

           期望风险是模型关于联合分布的期望损失，经验风险是模型关于训练集样本的平均损失，根据大数定律，当样本容量N趋于无穷时，经验风险趋于期望风险，所以可以用经验风险估计期望风险，但由于样本量不足，需要对经验风险进行校正，常用的策略是经验风险最小化和结构风险最小化。

           由上式可知，经验风险最小化就是求解优化下式：

          

           当样本容量足够大时，经验风险最小化能保证很好的效果，在实际中被广泛采用，比如极大似然估计就是一个例子；当模  型是条件概率分布，损失函数是对数函数时，经验风险最小化就等价于极大似然估计；而当样本量很小时，会产生过拟合结构风险最小化就是防止过拟合的策略，它是在经验风险上加了表示模型复杂度的正则化项，定义如下：

          

           模型越复杂，复杂度函数J(f)就越大，反之则越小，复杂度表示了对复杂模型的惩罚；结构风险小需要经验风险与模型复   杂度同时小，结构风险小的模型往往对训练数据及未知的测试集都有较好的预测。贝叶斯估计中的最大后验概率估计就是结构风险最小化的一个例子，当模型是条件概率分布，损失函数是对数损失函数，模型复杂度由模型的先验概率表示时结构风险最小化就等价于最大后验概率估计。

（3）算法：学习模型的具体计算方法，通常为最优化问题的求解

3. 模型的评估与选择

（1）训练误差与测试误差：都是基于损失函数的误差

         训练误差是模型关于训练集数据的平均损失：

    

         测试误差是模型关于测试集数据的平均损失：

       

（2）过拟合现象：学习时选择的模型所包含的参数过多，导致该模型对已知数据预测很好，对未知数据预测很差。

         训练误差和测试误差存在如下图的关系，即当模型复杂度增大时，训练误差会逐渐减小并趋于0，而测试误差会先减小，到最小值时增大，当模型选择复杂度过大时，过拟合现象就会发生。

         

         防止过拟合的方法可参考博客：https://blog.csdn.net/Left_Think/article/details/77684087

（3）正则化：是结构风险最小化策略的实现，是在经验风险上加一个正则化项，正则化项一般是模型复杂度的单调递增函数，模型越复杂，正则化值越大，正则化形式如下：

      

        式中，第一项是经验风险，第二项是正则化项，常用的正则化项有L1和L2范数：

        关于L1与L2具体定义和区别请参考博客：https://blog.csdn.net/zl3090/article/details/82667614

（4）交叉验证：将数据集分为训练集、验证集和测试集，训练集用于训练模型，验证集用于模型选择，测试集用于最终学习方   法的评估。在学到的不同复杂度的模型中，选择对验证集有最小预测误差的模型。

         a. 简单交叉验证：随机将数据分为两部分，一部分训练集，一部分测试集（通常70%，30%），然后在各种条件（如不同   的参数个数）训练模型，在测试集上评价各个模型的测试误差，选出测试误差最小的模型。

         b. S折交叉验证：随机将数据分为S个互不相交的大小相同的子集，然后用S-1个子集的数据训练模型，余下的测试，这一   过程对可能的S种选择重复进行，最后选出S次测评中平均测试误差最小的模型。

         c. 留一交叉验证：是S折交叉验证的特殊情况，S=N（样本容量），每次只留一个样本测试，用于数据缺乏的情况。

（5）泛化能力：由该方法学习到的模型，对未知数据的预测能力。如果学到的模型是，那么用这个模型对未知数据预测的误差即为泛化误差，泛化误差就是所学到的模型的期望风险：

        

        泛化误差的上界：用于比较两种学习方法的优劣，泛化上界是样本容量的函数，样本容量增加时，泛化上界趋于0，它是假设空间容量的函数，假设空间容量越大，模型就越难学，泛化误差上界就越大。

        泛化误差上界的定义：对于二分类问题，当假设空间是有限个函数集合时，对其中的任意一个函数，至少以概率1-δ，以下不等式成立：

        

        不等式左边是泛化误差，右边是泛化误差上界，右边第一项是训练误差，训练误差越小，泛化误差就越小，第二项是N的单调递减函数，当N趋于无穷时趋于0，同时也是阶的函数,d为假设空间的个数，假设空间的值越多，其值越大。

（6）生成模型与判别模型

         生成模型：由数据学习联合概率分布P(X,Y), 然后求出条件概率分布P(Y|X)作为预测的模型，

          

         这类方法之所以称为生成方法是因为模型表示了给定输入X产生输出Y的生成关系，典型的生成模型有朴素贝叶斯法和隐马尔科夫模型。

         判别模型：由数据直接学习决策函数f(X)或者条件概率分布P(X|Y)作为预测的模型，判别模型关心的给定输入X，预测输出 Y，常用的有，感知机，决策树，K邻近法，逻辑回归，SVM等。

         生成模型与判别模型的主要区别参考博客：https://blog.csdn.net/zl3090/article/details/82683889

4. 分类问题、标注问题与回归问题

（1）分类问题：

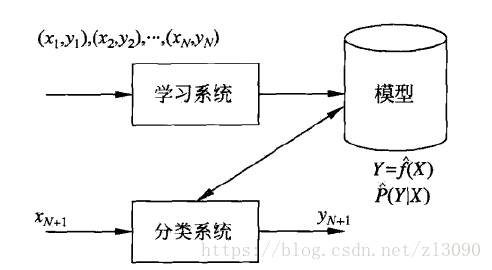
         分类器：监督学习从数据中学习的一个分类模型或者决策函数

         分类：分类器对新的输入进行输出的预测

  

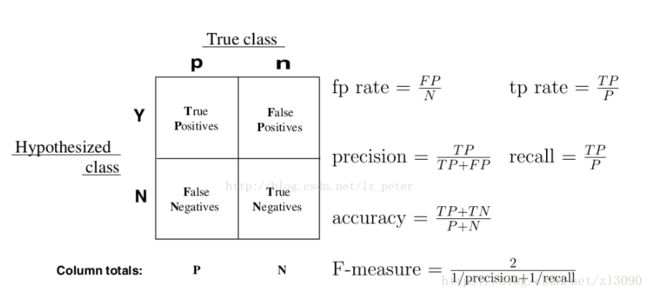
        评价分类器性能的一般指标是准确率（accuracy），定义是对于给定测试集的数据，分类器正确分类的样本数与总样本数之比，对于二分类问题，常用的指标有精确率（precision）与召回率（recall），定义如下（来源网络）：

详细精确率、召回率、ROC、AUC指标请参见博客：https://blog.csdn.net/zl3090/article/details/82684205

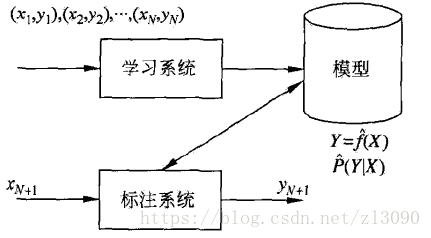
（2）标注问题：学习一个模型，使它能够对观测序列给出标记序列作为预测，是分类模型的推广

         

       标注问题与分类问题的评价指标一样，常用的统计学习方法有：隐马尔可夫模型，条件随机场

       标注问题在信息抽取，自然语言处理领域被广泛应用

（3）回归问题：预测输入变量与输出变量之间的关系

        

       回归问题按照输入变量的个数，分为一元回归和多元回归，按照输入变量和输出变量的关系分为线性回归和非线性回归。

       回归学习最常用的损失函数是平方损失函数，在此情况下，回归问题可以由著名的最小二乘法求解。

参考文献：

《统计学习方法》 李航