【吴恩达机器学习】第六章 Octave/Matlab教程

基本操作

% 是注释
语句后面加分号表示不打印结果
帮助函数是help 可以输入help 要询问的函数 然后键入q就可以退出
who 当前octave在内存中存储的所有变量
whos 更详细的显示变量信息
clear 变量 删除内存中的此变量

基本数学运算

逻辑运算

变量

向量和矩阵
①生成矩阵的方法：
size() 返回矩阵的大小
size(A,1) 返回A矩阵的行数
size(A,2) 返回A矩阵的列数
length() 返回矩阵或向量最大维度的大小

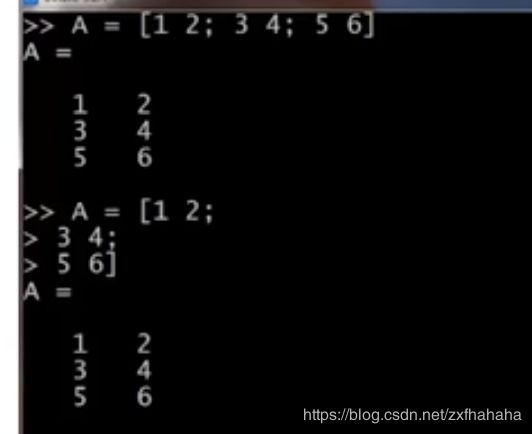
ones(m,n)
zeros同理只不过元素值为0

rand生成的是介于0到1之间的随机值

randn生成的随机值服从高斯分布/正态分布

eye(n)表示生成n行n列的单位矩阵即n阶单位矩阵

② 生成向量

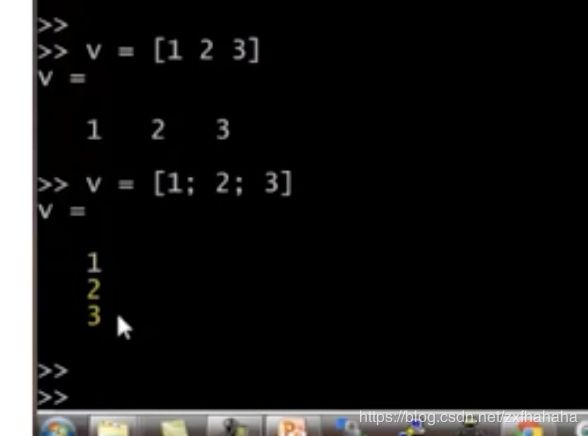
从1开始，步长为0.1，一直增加到2

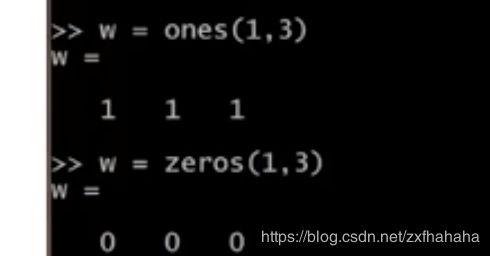
ones(1,n)是行向量，ones(m,1)是列向量
zeros同理，只不过元素值是0

移动数据

在文件系统中加载和查找数据

pwd命令 显示当前的路径即octave的当前所在路径
cd命令可以改变当前路径
ls 列出当前路径上的文件

①load 把数据读入octave

②储存数据 save
save hello.mat v %save将使变量v保存为一个名为hello.mat的文件 mat是压缩的二进制形式
save hello.txt v -ascii %这样就会把数据存储成文本文档

操作数据

① 索引
A(i,j) %输出矩阵A的第i行第j列位置上的元素
A(i,:) %输出矩阵A的第i行上所有的元素
A(:,j) %输出矩阵A的第j列上所有的元素

② 对矩阵的操作

改变矩阵某一列的值

给A在右边附加一列列向量

把A中所有的元素放入一个单独的列向量

C=[A B] 或者 C=[A,B] 把矩阵A和B结合起来，A在左边B在右边
C=[A;B] 把矩阵A和B结合起来，A在上边B在下边

计算数据

矩阵运算

① 矩阵乘法
C=A*B %A和B两个矩阵相乘
②矩阵元素的运算
C=A.*B %A和B上对应位置上的元素相乘 .一般用于元素的运算
C=A.^2 %对A的每个元素进行平方
1./A %对矩阵的每个元素求导数
③得到矩阵的对角线元素
A.*eye(n)
④矩阵转置
A' 得到A的转置矩阵
⑤ 求矩阵的逆矩阵
pinv(A)

数学函数

log(v) %对v中的所有元素进行求对数运算
exp(v) %以e为底，以v中的所有元素为指数的幂运算
abs(v) %求v中所有元素的绝对值
max(v) %返回v中最大的元素
max(A,[],1) 和max(A)%返回A中每一列的最大值
max(A,[],2) %返回A中每一行的最大值
max(max(A)) 和max(A(:)) 求矩阵A的最大值
[val,ind] = max(v) %返回的val是最大元素的值，ind是最大值的索引
sum(a) %a中所有元素的和
prod(a) %a中所有元素的乘积
floor(a) %对a中所有元素向下取整
ceil(a) %对a中所有元素向上取整
rand(n) %得到nxn的随机矩阵
magic(n) %生成n阶幻方矩阵，任意行 列 对角线上的元素加起来都等于相同的值
flipup(A) %使矩阵A垂直翻转

对矩阵的操作1表示列，2表示行
如sum(A,1)表示对每个列的元素求和

想对向量中的每个元素都加1课进行如下操作：
v+ones(length(v),1) 或者直接v+1
对应元素比较
a<3
find(a<3) 找到a中小于3的元素的索引

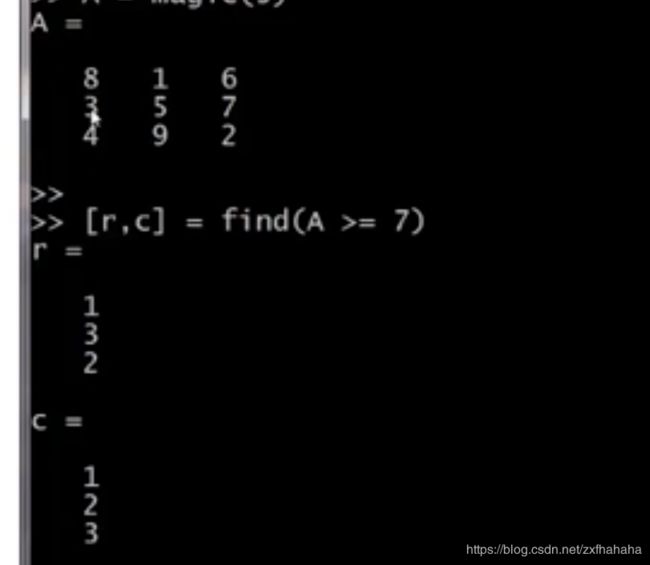
[r,c]=find(A>=7) %返回矩阵A中大于等于7的元素的行和列的数值

数据绘制

hold on在旧的图像上绘制新的图像
figure(n)为图像标号为n
close关闭图像
clf 清楚图像（得到一块白板

①plot
绘制正弦函数和余弦函数

t=[0:0.01:0.98] #生成0到0.98 步长为0.01的数列
y1=sin(2*pi*4*t)
y2=cos(2*pi*4*t)
plot(t,y1) %绘制正弦函数 横轴是变量t，纵轴是y1
hold on % 在旧图像绘制新图像
plot(t,y2,'r') %绘制余弦函数 r表示用红色绘制
xlabel('time') %x轴的名称 
ylabel('value') %y轴的名称
legend('sin','cos') %图例
title('my plot') %图的标题
print -dpng 'Myplot.png' #保存图片到当前路径
close %关闭图像

用subplot将画板分割

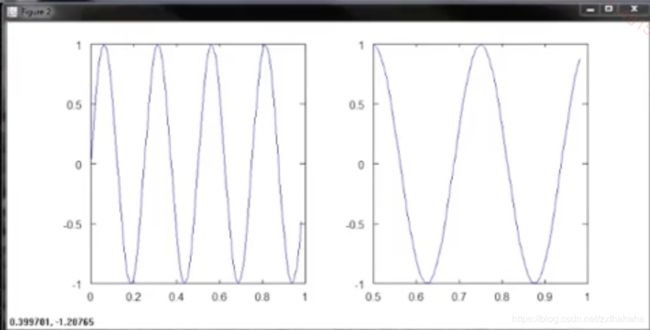
subplot(1,2,1)  %将图像分成1*2的网格，用第一个格子
plot(t,y1) 
subplot(1,2,2) %用第二个格子
ploot(t,y2)

改变轴的刻度axis

axis([0.5 1 -1 1]) %将x轴的范围改为0.5到1，将y轴的范围改为-1到1

②可视化矩阵

imagesc(A)

imagesc(A)
colorbar
colormap gray

控制语句：for,while,if语句 定义和使用函数

for语句

①

for i=1:10,
    v(i)=2^i;  %这里的缩进没有意义
end;

② 设置索引

indices=1:10;
for i = indices,
      disp(i);
end;

while

①

i=1;
while i<=5,
      v(i)=100;
      i=i+1;
end;

②用break结束循环

i=1;
while true,
     v(i)=999;
     i=i+1;
     if i==6,
          break;
      end;
end;

if else

if v(1)==1,
   disp('值是1');
elseif v(1)==2,
   disp('值是2');
else
   disp('值不是1和2');
end;

定义和调用函数

在octave环境下定义函数，需要先创建一个文件：
①文件名字
用你的函数名命名，然后以.m的后缀结尾
②文件内容

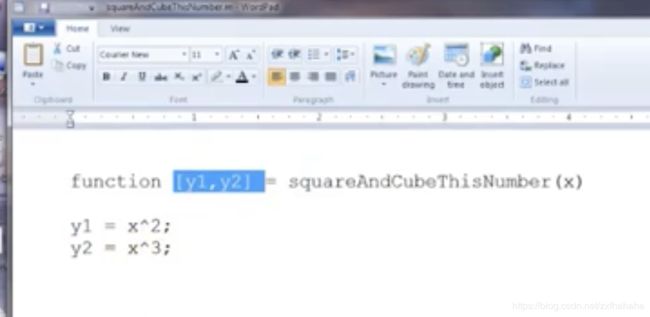
function y = squareThisNumber(x) %告诉octave我想返回一个值，将它存在变量y里；函数名和自变量x
y=x^2  %函数内容

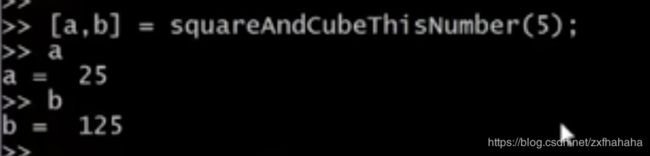
③在octave调用函数
先设置当前路径到存定义函数的文件

cd '函数文件所在的目录'
squareThisNumber(5) 

octave允许定义可以返回多个值的函数

eg:定义一个函数去计算损失函数J(theta)

%把数据放到octave里
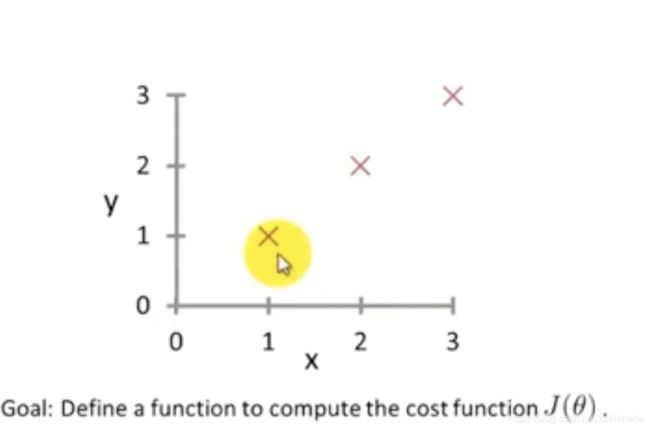
x = [1 1;1 2;1 3]  %设计矩阵X 第一列表示x0的值，第二列是训练样本x的值
y = [1,2,3]  
theta = [0;1] % 设计theta0是0 theta1是1

在文件中定义函数

矢量

左边没有用向量化，右边用了向量化

没看懂

使用向量化实现线性回归相比用for循环运行速度会快很多