统计学三大相关系数之皮尔森(pearson)相关系数
最早接触pearson相关系数时,是和同学一起搞数学建模,当时也是需要一种方法评价两组数据之间的相关性,于是找到了皮尔森(pearson)相关系数和斯皮尔曼(spearman)相关系数。其实,还有一种相关系数肯德尔(kendall)相关系数。在这三大相关系数中,spearman和kendall属于等级相关系数亦称为“秩相关系数”,是反映等级相关程度的统计分析指标。今天暂时用不到,所以现在只做pearson的相关研究。
首先放上公式:
公式定义为: 两个连续变量(X,Y)的pearson相关性系数(Px,y)等于它们之间的协方差cov(X,Y)除以它们各自标准差的乘积(σX,σY)。系数的取值总是在-1.0到1.0之间,接近0的变量被成为无相关性,接近1或者-1被称为具有强相关性。
皮尔森相关系数是衡量线性关联性的程度,p的一个几何解释是其代表两个变量的取值根据均值集中后构成的向量之间夹角的余弦。
根据以上公式,python3实现代码:
def pearson(vector1, vector2):
n = len(vector1)
#simple sums
sum1 = sum(float(vector1[i]) for i in range(n))
sum2 = sum(float(vector2[i]) for i in range(n))
#sum up the squares
sum1_pow = sum([pow(v, 2.0) for v in vector1])
sum2_pow = sum([pow(v, 2.0) for v in vector2])
#sum up the products
p_sum = sum([vector1[i]*vector2[i] for i in range(n)])
#分子num,分母den
num = p_sum - (sum1*sum2/n)
den = math.sqrt((sum1_pow-pow(sum1, 2)/n)*(sum2_pow-pow(sum2, 2)/n))
if den == 0:
return 0.0
return num/denvector1 = [2,7,18,88,157,90,177,570]
vector2 = [3,5,15,90,180, 88,160,580]
运行结果为0.998,可见这两组数是高度正相关的。
现在用股票数据试下:
with open('hs300_399300.csv', 'r') as db01:
reader = csv.DictReader(db01)
column1 = [float(row['收盘价']) for row in reader]
# 再次读取全部文件需要将文件指针移到文件开始处
db01.seek(0)
reader = csv.DictReader(db01)
column2 = [float(row['最高价']) for row in reader]
# 取前30天的数据
list1 = column1[:30]
list2 = column2[:30]
print(pearson(list1, list2))
pearson系数为0.986,表明收盘价和最高价竟然高度正相关。分析原因:基数大(3600),数据变化小(变动不超过三位数)。
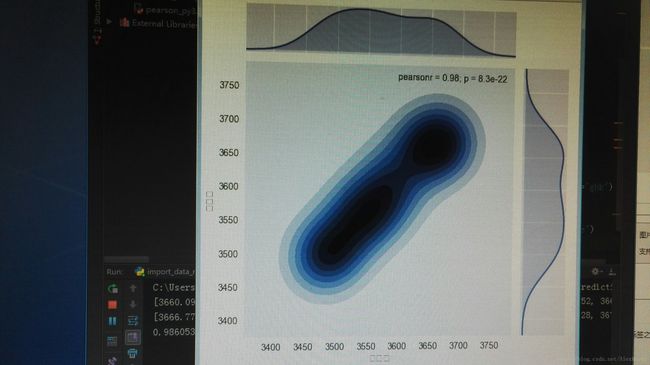
接下来用seaborn.jointplot()画图。jointplot是画两个变量或者单变量的图像,是对JointGrid类的实现。x,y为DataFrame中的列名或者是两组数据,data指向dataframe ,kind是你想要画图的类型,stat_func 用于计算统计量关系的函数,kind 的类型scatter,reg,resid,kde,hex.
# 之前一直遇到utf-8不能识别报错,后来的转换方法还是在国外论坛找到的,如下
import csv
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
stock = pd.read_csv("hs300_399300a.csv", index_col=0, encoding="gbk")
sns.jointplot(x="收盘价", y="最高价", data=stock, kind="reg")
plt.show()
只能这样上传图片,先凑合看看,先将csv文件截取了前30条数据,然后jointplot画图的类型从左到右分别为reg,kde,hex.图像更加直观,收盘价和最高价果然是高度正相关,原因基数太大,每日变化幅度太小。